Что нужно знать о законах алгебры логики — основные сведения
Что такое алгебра логики
Алгебра высказываний (алгебра логики) представляет собой главу математической логики, главной задачей которой является изучение логических действий с высказываниями и механизмов трансформации сложных высказываний.
В процессе поиска решений распространенных задач логики и их упрощения необходимо переводить формулы, которые являются результатом формализации условий, в более простую форму. С этой целью прибегают к эквивалентным преобразованиям с отсылкой к ключевым законам логики с доказательствами.
Современная интерпретация алгебраической логики направлена на анализ действий с высказываниями с использованием тождеств и теорем.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Высказывание является предположением, для которого характерно единственное качество в форме истинности значения (истина, ложь).
Классическая алгебра логики предусматривает наличие в одно и то же время у высказывания только одного из двух истинных значений:
- истина;
- ложь.
С другой стороны, алгебра логики также изучает высказывания в виде функций, принимающих истинные или ложные значения, исходя из определенного значения переменной, которая входит в высказывание, то есть в функцию.
Основные законы алгебры логики и их формулы
Алгебра логики базируется на высказываниях, или мышлениях. Они формируются над множеством В, \(\lnot\), \(\land\), \(\lor\), 0, 1, где В обозначает непустое множество, над компонентами которого возможны следующие операции:
- \(\lnot\) отрицание (унарная операция, инверсия);
- \(\land \) конъюнкция (бинарная);
- \(\lor \) дизъюнкция (бинарная).
Константами можно назвать логический ноль 0 и логическая единица 1.
Дизъюнкт обозначает пропозициональную формулу, которая является дизъюнкцией одного или более литералов.
Запишем дизъюнкт:
\(x_{1}\lor \neg x_{2}\lor x_{4}.\)
Конъюнкт представляет собой пропозициональную формулу в виде конъюнкции одного или более литералов.
Запишем конъюнкт:
\(x_{1}\land \neg x_{2}\land x_{4}.\)
Унарную операцию отрицания, или инверсию, в процессе записи формул представляют, как значок перед операндом \(\lnot x\). Другим вариантом обозначения является черта над операндом \(\bar {x}\). Второй вариант записи отличается компактностью, но меньшей заметностью.
Рассмотрим подробнее основные логические операции. Начнем с конъюнкции. Логическое умножение построено на паре высказываний. Таким образом, формируется новое суждение. Оно будет истиной тогда, когда начальные высказывания истинны. Существуют следующие формы записи конъюнкции:
- A и B;
- A \(\perp\) B;
- A \(\cdot\) B;
- A & B.
А обозначает высказывание: «Закончился дождь». B соответствует высказыванию: «Из-за туч выглянуло солнце». Новое суждение: «Закончился дождь, и из-за туч выглянуло солнце», станет истиной лишь в том случае, когда А и B являются истинными.
Проанализируем дизъюнкцию. Результатом логического сложения пары начальных суждений является новое высказывание. Полученное суждение ложно при ложных начальных высказываниях. Графически дизъюнкцию обозначают таким образом:
- A или B;
- A \(\vdash\) B;
- A|B;
- A+B.
Высказывание A обозначает: «В парке можно покататься на роликах». Суждение B обозначает: «В парке можно просто погулять». Новое высказывание: «В парке можно покататься на роликах или просто погулять», является ложным, если А и В ложные.
Логическое отрицание подразумевает соотнесение каждого суждения с высказыванием, противоположным начальному. Представить инверсию можно в таком виде:
- не А;
- \(\urcorner\) А;
- \(\bar{А}\).
Суждение A обозначает: «За окном бушует вьюга». Суждение \(\bar{А}\) обозначает: «Неверно, что за окном бушует вьюга».
С помощью таблицы истинности формируют совершенные формы. Согласно правилу для составления дизъюнкции, для любого из комплексов переменных с истинной функцией можно записать минтерм ранга n>. При этом нулевые переменные следует рассматривать с отрицанием. Какие-либо конъюнктивные термы связывают дизъюнктивно. СДНФ для номеров N=1, 3, 6, 7:
\(f(a,b,c)=\overline a\overline bc+\overline abc+ab\overline c+abc\).
С помощью таблицы истинности составляют конъюнкции. При этом для любого комплекса переменных с ложным значением функции можно представить дизъюнктивный терм ранга n. В нем переменные со значениями, равными единице, на рассматриваемом комплексе берут с отрицанием. Какие-либо макстермы объединяют конъюнктивно. СКНФ для номеров наборов N=0, 2, 4, 5:
\(f(a,b,c)=(a+b+c)(a+\overline b+c)(\overline a+b+c)(\overline a+b+\overline c)\).
Алгоритм действий для составления таблицы истинности:
- Вычисление количества переменных элементов функции.
- Определение общего числа действий в выражении.
- Упорядочение логических действий с учетом раскрытия скобок.
- Вычисление числа столбцов в табличной форме с помощью суммирования количества переменных и количества действий.
- Согласно определенному порядку из третьего шага данного алгоритма, заполнение шапки таблицы переменными и действиями.
- Расчет числа строк в таблице, не считая шапку, с помощью формулы m=2n.
- Запись комбинаций вводных переменных, которые сформулированы, как целый ряд двоичных чисел от 0 до 2n−1 с разрядом n.
- Последовательное заполнение столбцов таблицы с параллельным выполнением логических операций.
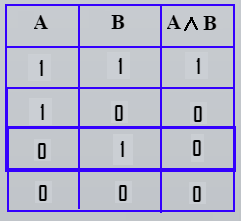
Попробуем составить таблицу истинности. Представим, что в некотором выражении A&B пара переменных и единственное действие в форме конъюнкции. Число столбцов в этом случае равно трем:
- A;
- B;
- A&B.
Руководствуясь рассмотренным ранее алгоритмом действий, составим таблицу:
Свойства и применение законов алгебры логики
Перечислим ключевые свойства:
- Коммутативность: \(x\circ y=y\circ x,\circ \in \{\land ,\lor ,\oplus ,\sim ,\mid ,\downarrow \}\).
- Идемпотентность: \(x\circ x=x,\circ \in \{\land ,\lor \}\).
- Ассоциативность: \((x\circ y)\circ z=x\circ (y\circ z),\circ \in \{\land ,\lor ,\oplus ,\sim \}\).
- Дистрибутивность конъюнкций и дизъюнкции по отношению к дизъюнкции, конъюнкции и суммы по модулю два соответственно: \(x\land (y\lor z)=(x\land y)\lor (x\land z), x\lor (y\land z)=(x\lor y)\land (x\lor z), x\land (y\oplus z)=(x\land y)\oplus (x\land z)\).
- Законы де Моргана: \({\overline {x\land y}}={\bar {x}}\lor {\bar {y}}, {\overline {x\lor y}}={\bar {x}}\land {\bar {y}}\).
- Законы поглощения: \(x\land (x\lor y)=x, x\lor (x\land y)=x.\)
Другие свойства:
- \(x\land {\bar {x}}=x\land 0=x\oplus x=0\);
- \(x\lor {\bar {x}}=x\lor 1=x\sim x=x\rightarrow x=1\);
- \(x\lor x=x\land x=x\land 1=x\lor 0=x\oplus 0=x\);
- \(x\oplus 1=x\rightarrow 0=x\sim 0=x\mid x=x\downarrow x={\bar {x}};\)
- \({\bar {\bar {x}}}=x\), данная запись обозначает инволютивность отрицания, закон снятия двойного отрицания;
- \(x\oplus y=x\land {\bar {y}}\lor {\bar {x}}\land y=(x\lor y)\land ({\bar {x}}\lor {\bar {y}})\);
- \(x\sim y={\overline {x\oplus y}}=1\oplus x\oplus y=x\land y\lor {\bar {x}}\land {\bar {y}}=(x\lor {\bar {y}})\land ({\bar {x}}\lor y)\);
- \(x\rightarrow y={\bar {x}}\lor y=x\land y\oplus x\oplus 1\);
- \({\displaystyle x\lor y=x\oplus y\oplus x\land y}x\lor y=x\oplus y\oplus x\land y\);
- \(x\mid y={\overline {x\land y}}={\bar {x}}\lor {\bar {y}}\);
- \(x\downarrow y={\overline {x\lor y}}={\bar {x}}\land {\bar {y}}\).
Логика суждений выполняет функцию ключевого математического инструмента, который используют при разработке компьютеров. Данные закономерности достаточно просто трансформировать в битовую логику. Для обозначения истинности суждения используют один бит (0 обозначает ложь, 1 обозначает истину). В таком случае действие \(\neg\) имеет смысл вычитания из единицы:
- \(\lor\) — немодульного сложения;
- & — умножения;
- \(\leftrightarrow \)— равенства;
- \(\oplus \)— в буквальном смысле сложения по модулю 2 (исключающее Или — XOR);
- \(\mid\) — не превосходства суммы над 1 (то есть A \(\mid\) B = (A+B)<=1).
Таким образом, булеву алгебру получилось обобщить от логики высказываний с помощью использования аксиом, которые характерны для логики суждений. В результате сформированы, к примеру, логика кубитов, тройственная логика, комплексная логика и другие.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так