Формула длины окружности через диаметр, радиус и площадь
Что такое окружность
Окружность представляет собой кривую линию, достаточно распространенную в окружающем нас мире. Ее рассматривают в рамках какой-либо плоскости. Изобразить окружность можно с помощью циркуля или веревки, один конец которой фиксируют в одной точке. В том и другом варианте начертания точки окружности равноудалены от центра.
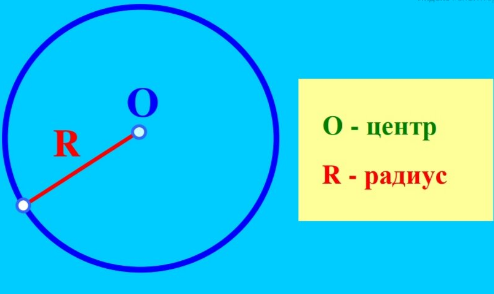
Некий отрезок, соединяющий центральную точку и такую точку, которая лежит на окружности, принято считать радиусом. Если перевести этот термин с латинского языка, то получится «спица колеса». Данная ассоциация вполне логична, так как, по сути, окружность является математической моделью колеса.
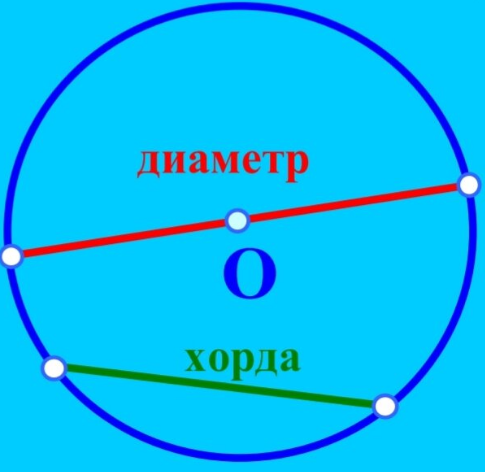
Соединяя пару точек, расположенных на окружности, получают хорду. В греческом языке хорда понимается как «струна». В том случае, когда этот отрезок пересекает центральную точку окружности, его называют диаметром. Протяженность диаметра ровно в два раза больше по сравнению с размером радиуса окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: yandex.ru
Источник: yandex.ru
Окружностью называют множество точек, расположенных на некой плоскости, которые равноудалены от одной заданной точки.
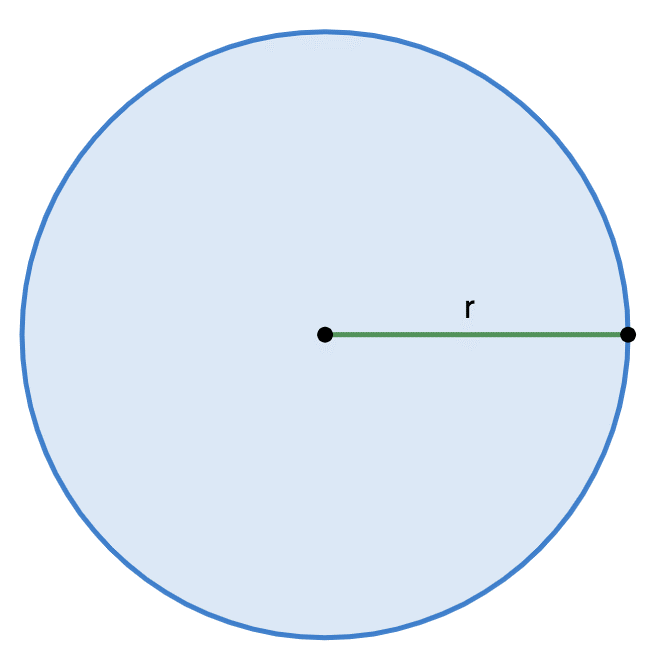
Радиус окружности представляет собой отрезок с началом, совпадающим с центральной точкой, и концом, расположенным в любой из точек рассматриваемой окружности.
Хорда является отрезком, который соединяет пару каких-либо точек окружности.
Диаметром называют хорду, проходящую через центральную точку окружности.
Источник: yandex.ru
Источник: yandex.ru
Расчет длины окружности: формулы
Длина окружности определяется, как протяженность плоской кривой, которая является замкнутой и ограничивает круг.
Известно, что окружность играет роль границы для круга. В таком случае, можно сделать вывод о соответствии длины окружности частному случаю периметра. Вспомним из курса геометрии, что периметром обозначают совокупную протяженность границы какой-либо фигуры.
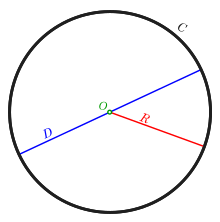
Представим на рисунке, как выглядит длина произвольной окружности С, диаметр которой равен D, радиус составляет R, а в качестве центральной выбрана точка О:
Источник: ru.wikipedia.org
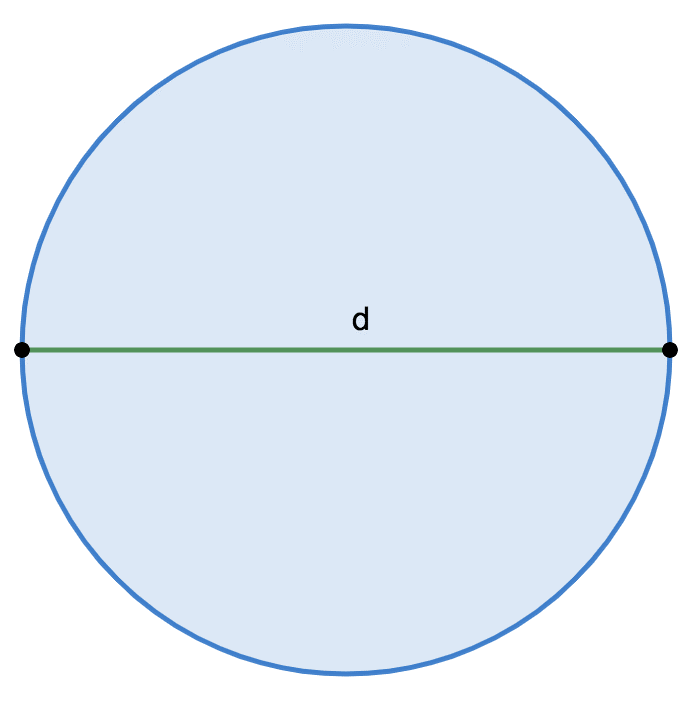
Через диаметр
Периметр или длину окружности можно вычислить, если известна величина ее диаметра. При этом используют формулу, согласно которой диаметр следует умножить на число \(\pi\):
\(С = \pi \cdot d\)
Источник: microexcel.ru
Эта формула пригодится при решении разнообразных геометрических задач, а также необходима, чтобы упростить вычисления физических и астрономических величин. В процессе расчетов нужно учитывать, что диаметр определяется, как радиус окружности, помноженный на два. Кроме того, принято округлять число \(\pi\). При вычислениях целесообразно принимать его за 3,14.
Через радиус
Если умножить на 2 произведение радиуса окружности и числа \(\pi\), то получится величина длины ее окружности. Формула при этом принимает следующий вид:
\(С = 2 \cdot \pi \cdot r\)
Источник: microexcel.ru
Через площадь
В некоторых задачах по условию может быть задана площадь окружности. Зная особую формулу, учащемуся не составит труда вычислить длину окружности таким методом:
\(C = \sqrt{4S\pi}\)
В данном случае площадь окружности обозначают буквой S.
Примеры решения задач
Имеется некая окружность с радиусом 12 см. Необходимо вычислить, чему равна длина этой окружности.
Решение
Зная, что вычислить длину окружности при известном ее радиусе можно по стандартной формуле, подставим в выражение числовые значения и запишем ответ:
\(C = 2 \cdot 3,14 \cdot 12 = 75,36\)
Ответ: 75,36 см.
Диаметр окружности равен 15 см. Нужно определить периметр круга, который ограничен этой окружностью.
Решение
Периметр круга в данном случае соответствует длине окружности. Вычислить искомую величину можно, зная диаметр окружности:
\(C = 3,14 \cdot 15 = 47,1\)
Ответ: 47,1 см.
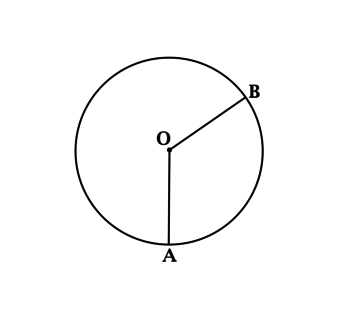
Окружность обладает длиной, равной 12. Ее центр обозначен буквой О. Угол \(\angle AOB\) составляет \(120^{\circ}\). С помощью точек А и В, которые принадлежат окружности, она делится на пару дуг. Требуется вычислить, во сколько раз длина максимальной из образованных дуг больше по сравнению с длиной меньшей.
Источник: shkolkovo.net
Решение
Известно, что отношение длин дуг соответствует отношению их градусных мер. Зная, что О является центральной точкой окружности, определим \(\angle AOB\), как центральный. Дуга по градусной мере меньше по сравнению с полуокружностью. Ее градусная мера соответствует градусной мере центрального угла, опирающегося на эту дугу. Меньшая дуга равна \(120^{\circ}\), а градусная мера максимальной дуги составляет \(240^{\circ}\). Таким образом:
\(240 \div 120 = 2\)
Ответ: 2.
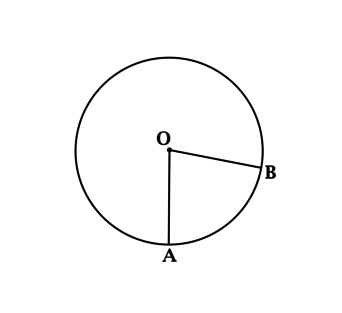
На рисунке изображена окружность с центральной точкой О. Длина этой окружности составляет 18 см. Сектор АОВ обладает площадью \(\dfrac{18}{\pi}см^2\). Требуется определить, чему равна длина дуги АВ рассматриваемого сектора.
Источник: shkolkovo.net
Решение
Запишем формулу для вычисления длины окружности при ее известном радиусе:
\(С = 2\pi R\)
Согласно условию задачи:
\(18 = 2\pi R\)
В таком случае:
\(R = \dfrac{9}{\pi}\)
Площадь сектора, градусная мера дуги которого составляет \(\alpha\), равна:
\(\pi R^2 \cdot \dfrac{\alpha}{360}\)
Тогда запишем выражение для расчета длины дуги с градусной мерой \(\alpha\):
\(2\pi R\cdot \dfrac{\alpha}{360}\)
Если умножить площадь сектора с дугой, равной \(\alpha\), на \(\dfrac{2}{R}\), то получится определить длину дуги с градусной мерой \(\alpha\). В результате длина дуги АВ рассматриваемого сектора составляет:
\(\dfrac{18}{\pi} \cdot \dfrac{2\pi}{9} = 4\)
Ответ: 4 см.
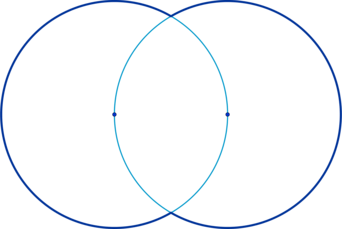
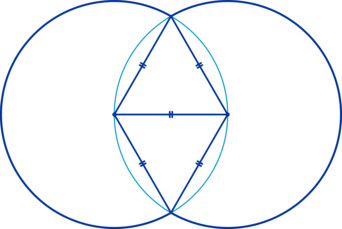
На рисунке изображено пересечение пары окружностей. Требуется вычислить длину внешней границы фигуры, которая получилась в результате. Длина окружности составляет 12.
Источник: shkolkovo.net
Решение
Проведем отрезок через центральные точки окружностей. Соединим центры этих фигур с точками, в которых окружности взаимно пересекаются. Заметим, что можно сформировать пару равносторонних треугольников со сторонами, равными радиусам рассматриваемых окружностей.
Источник: shkolkovo.net
Дуга, принадлежащая одной окружности, которая находится внутри сформированной фигуры, имеет опору в виде угла. Этот угол равен паре углов, принадлежащих равностороннему треугольнику, и составляет \(120^\circ\). Таким образом, длину этой дуги допустимо вычислить по следующей формуле:
\(\frac{C_{120^\circ}}{12} = \frac{120^\circ}{360^\circ} \Rightarrow C_{120^\circ} = 4\)
В результате длина внешней границы при пересечении окружностей составляет:
\(L = 2\cdot C - 2\cdot C_{120^\circ} = 2\cdot12 - 2\cdot 4 = 16\)
Ответ: 16.
Задача 6
На рисунке изображена окружность с некоторыми известными величинами. Требуется рассчитать меру \(\angle AOB\).
Источник: shkolkovo.net
Решение
Запишем, чему равна общая длина окружности:
С = 1 + 2 + 5 + 10 = 18
В таком случае упрощается нахождение искомого угла:
\(\frac{C_{\angle AOB}}{C} = \frac{\angle AOB}{360^\circ} \Rightarrow \frac{5}{18} = \frac{\angle AOB}{360^\circ} \Rightarrow \angle AOB = 100^\circ\)
Ответ: 100.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так