Применение диаграмм Эйлера-Венна в дискретной математике
Диаграмма Эйлера-Венна – что это такое
В современной математике выделяют два основных направления — дискретную и непрерывную математику.
При решении и исследовании задач в дискретной математике оперируют понятием множества.
Множество — совокупность объектов, которые объединены по одному или нескольким общим признакам. Например, множество преподавателей, множество автомобилей. Объекты множества называют его элементами.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Множества обозначают прописными латинскими буквами, а элементы — строчными.
Также выделяют подмножество и универсальное множество.
Подмножеством множества А называют такое множество B, все элементы которого одновременно принадлежат множествам А и В.
Универсальное множество — множество, которое содержит в себе все возможные элементы и множества. Универсальное множество обозначают латинской буквой U.
В теории множеств для наглядного представления множеств и операций над ними используют диаграмму Эйлера-Венна.
Диаграмма Эйлера-Венна — изображение в виде схемы операций над множествами, входящими в состав универсального множества.
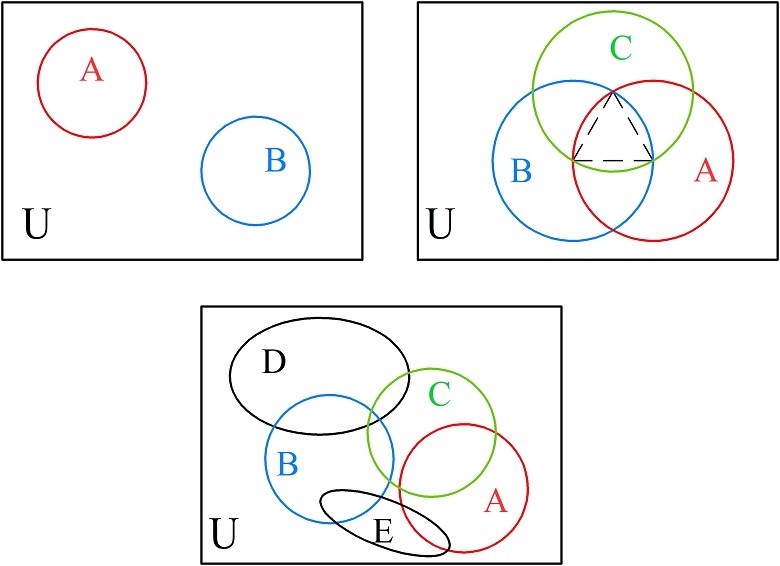
При построении диаграммы универсальное множество изображают в виде прямоугольника, внутри которого располагают множества. Если в решаемой задаче количество множеств меньше трех, их обозначают в виде окружностей. В случае, если число множеств равно трем, они изображаются в виде трех равных кругов, при этом центры окружностей располагают в вершинах равностороннего треугольника, а радиус окружности задают равным стороне треугольника. Если множеств больше трех, допускается изображать их в виде эллипсов или произвольных замкнутых фигур.
При задании множества на диаграмме фигура, отображающая это множество, должна быть замкнутой.
С помощью диаграммы Эйлера-Венна можно:
- выполнять различные операции над множествами (объединение, пересечение, вычитание и т. д.);
- доказывать логические неравенства.
Операции над множествами при помощи диаграмм Эйлера-Венна
Суть выполнения различных операций над множествами с помощью диаграмм Эйлера-Венна заключается в том, что область, соответствующую данной операции, штрихуют или заполняют цветом.
В том случае, если необходимо выполнить несколько операций, решением будет область, в которой совпали все штриховки.
Рассмотрим логические операции над множествами и их изображения на диаграмме Эйлера-Венна:
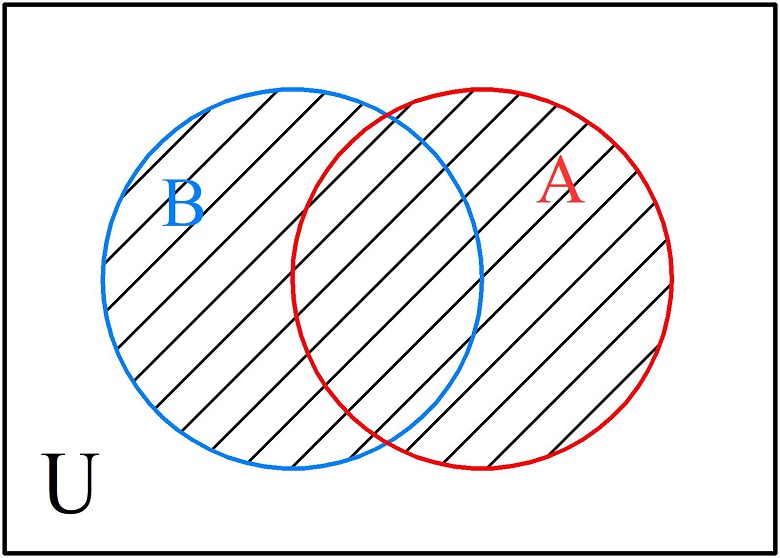
- Логическое сложение (объединение, дизъюнкция, операция «или») обозначается символом «\(\cup\)». Объединением \(A\;\cup\;\)B называют множество, включающее в себя элементы, которые принадлежат хотя бы одному из исходных множеств. При изображении на диаграмме полностью штрихуют фигуры складываемых множеств.
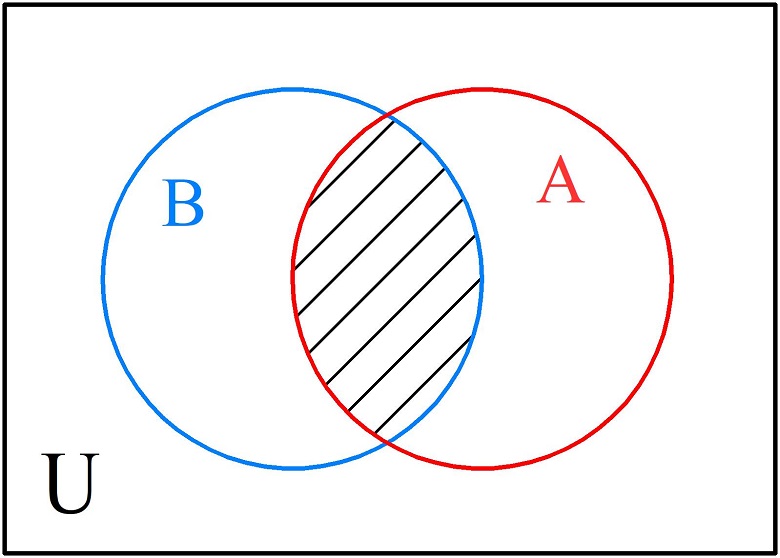
- Логическое умножение (пересечение, конъюнкция, операция «и») обозначается символом «\(\cap\)». Пересечением исходных множеств \(A\;\cap\);B называют множество, в которое входят элементы, принадлежащие одновременно всем исходным множествам. На диаграмме при выполнении логического умножения штрихуется область пересечения фигур.
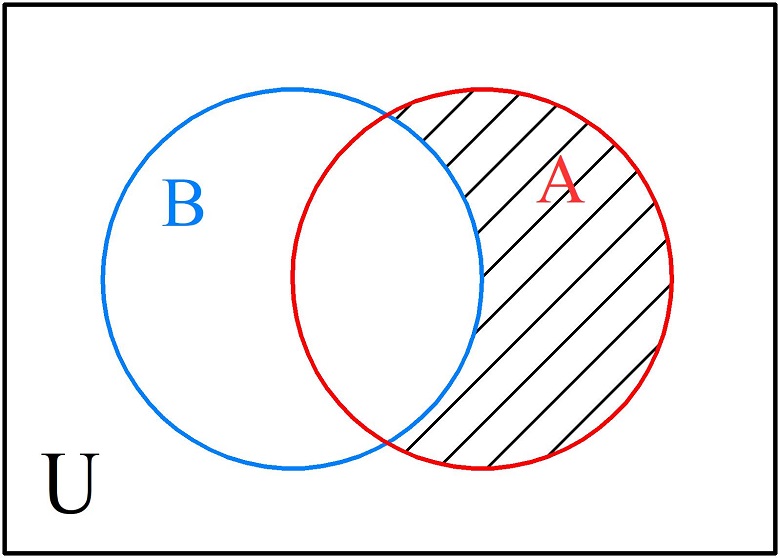
- Логическая разность обозначается символом «\» (иногда встречается обозначение «–»). Разностью исходных множеств \(A\;\backslash\);B называют множество, состоящее из элементов, содержащихся только в множестве А и не содержащихся в множестве В. На диаграмме разность обозначают через штриховку только той области множества А, которая не пересекается с множеством В.
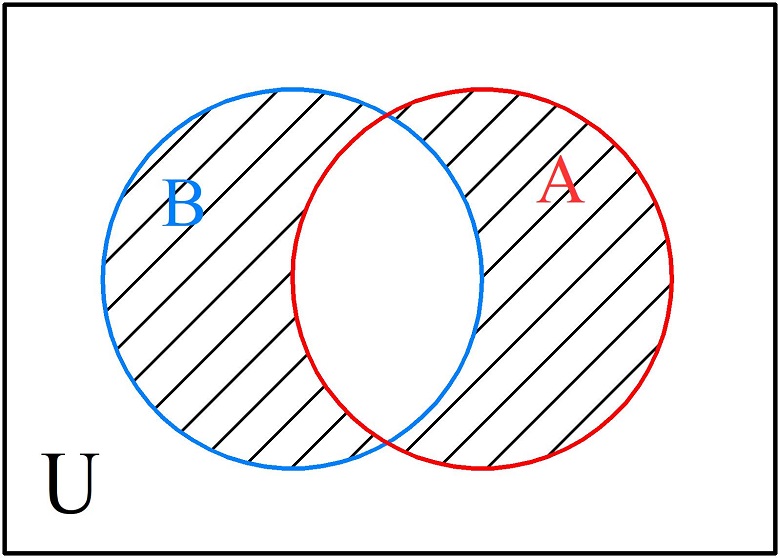
- Симметрическая разность множеств обозначается символом «+». Симметрическая разность множеств А+В есть множество элементов, которые принадлежат либо множеству А, либо множеству В. При изображении симметрической разности штрихуют области множеств, кроме области их пересечения.
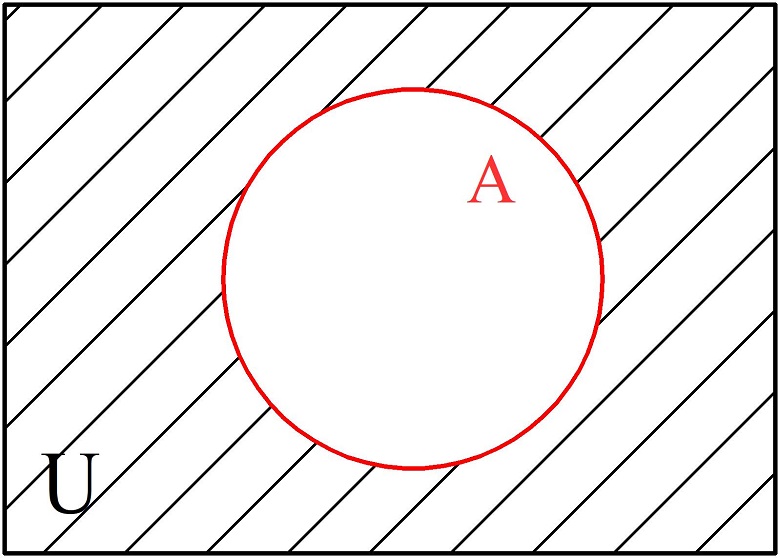
- Абсолютное дополнение (логическое отрицание, операция «не») обозначается верхней чертой над обозначением множества — «\(\overline А\)». Абсолютное дополнение — множество элементов, которые не входят в исходное множество. На диаграмме дополнение изображается в виде штриховки области универсального множества, исключая область исходного множества.
Логическая разность не обладает переместительным свойством, то есть \(A\;\backslash\;B\neq B\;\backslash\;A\).
Применение диаграмм Эйлера-Венна для доказательств логических равенств
Приведем небольшой алгоритм по доказательству логических равенств с помощью диаграмм Эйлера-Венна:
- Сначала исходное равенство разбивают на две части: левую и правую.
- Строят диаграмму для левой части равенства. Штрихуют области множеств, которые соответствуют результату выполнения указанных логических операций.
- Аналогично строят диаграмму для правой части и штрихуют области, соответствующие результату выполнения операций в правой части.
- Визуально сравнивают две получившиеся диаграммы. Делают вывод об истинности или ложности равенства.
Как применяются для поиска в информации в интернете
Работа с сетью Интернет, в частности поиск информации, знаком каждому. Поисковые запросы также можно изобразить в виде диаграммы Эйлера-Венна.
При вводе запроса в поисковую строку пользователь может использовать логические связки, аналогичные объединению (|) или пересечению (&). На основе запроса и использованных связок поисковый сервис выдаст результат.
Приведем небольшой пример.
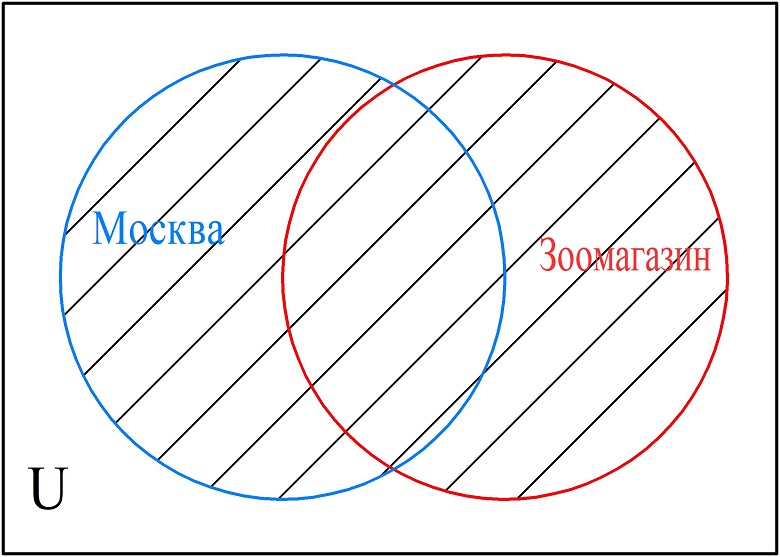
Построим диаграмму для случая, когда пользователь ввел запрос «Москва|зоомагазин». Поисковая система выдаст список страниц, на которых упоминаются либо два слова одновременно, либо хотя бы одно из запрашиваемых слов. Диаграмма Эйлера-Венна будет выглядеть следующим образом.
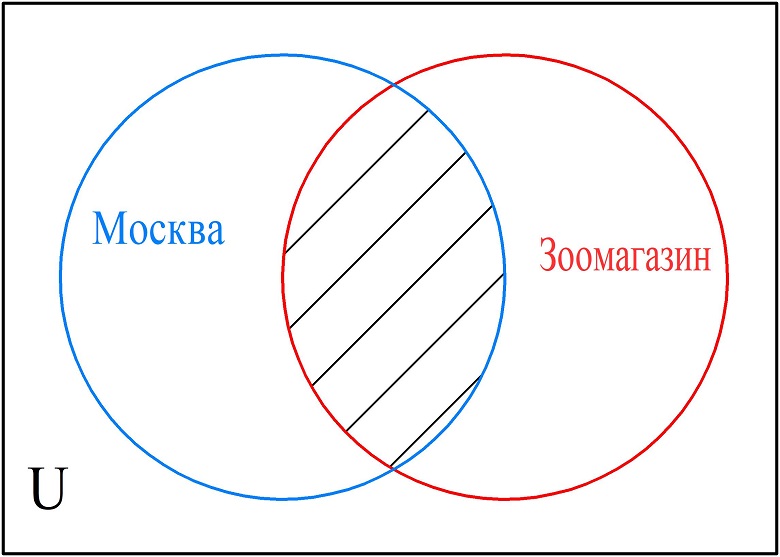
В случае, когда вводится запрос «Москва & зоомагазин», поисковая система предоставит перечень страниц, на которых оба слова встречаются одновременно.
Примеры задач с решением
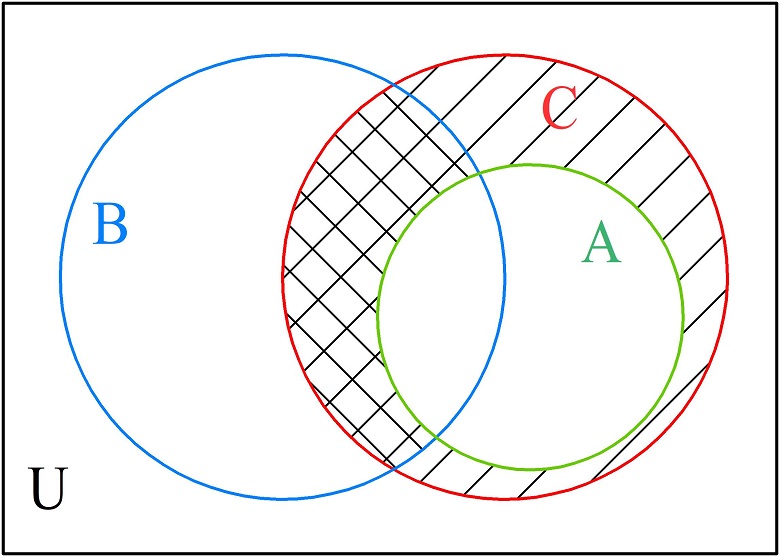
Даны три множества А, B и C. Известно, что множество А является подмножеством С. Построить диаграмму Эйлера-Венна для следующего выражения: (C\backslash A)\cap B.
Решение.
Так как А — подмножество С, обозначим его окружностью внутри множества С. Заштрихуем область (\(C\backslash A\)), а затем ее пересечение с множеством В.
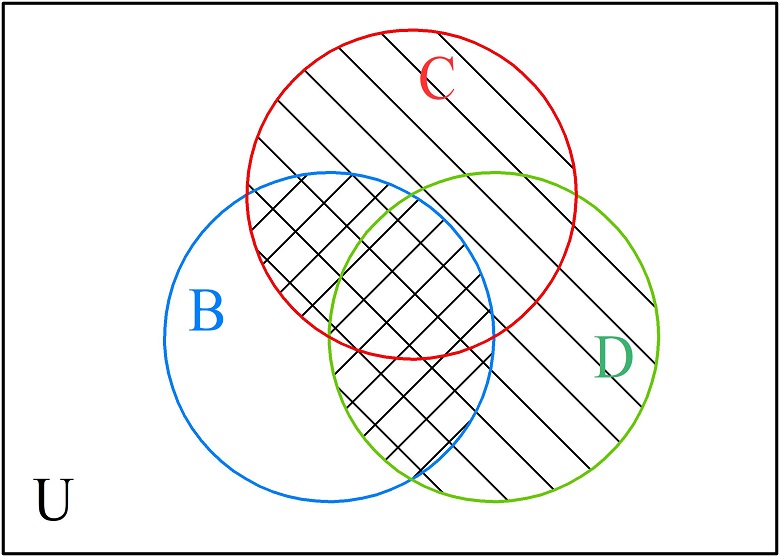
Даны четыре множества A, B, C, D. С помощью диаграммы Эйлера-Венна определить истинность или ложность следующего равенства: (\(D\cup C)\cap B=\overline{\left(A\cap B\cap C\right)}\)
Решение.
Построим диаграмму для левой части равенства и заштрихуем область, которая соответствует результату выполнения логических операций.
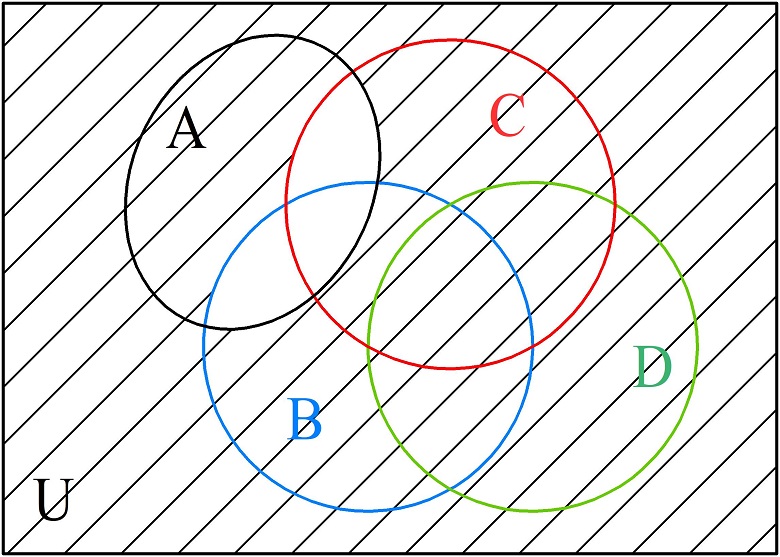
Аналогично построим диаграмму для правой части, добавив множество А. Штрихуем области, которые не являются пересечением множеств А и С, А и В.
При сравнении двух диаграмм очевидно, что равенство ложное.
Пользователь последовательно делает два запроса: «Браслет & золотой» и «Браслет|золотой». С помощью диаграммы Эйлера-Венна определить, на какой из двух запросов поисковая система предоставит большее количество страниц.
Решение.
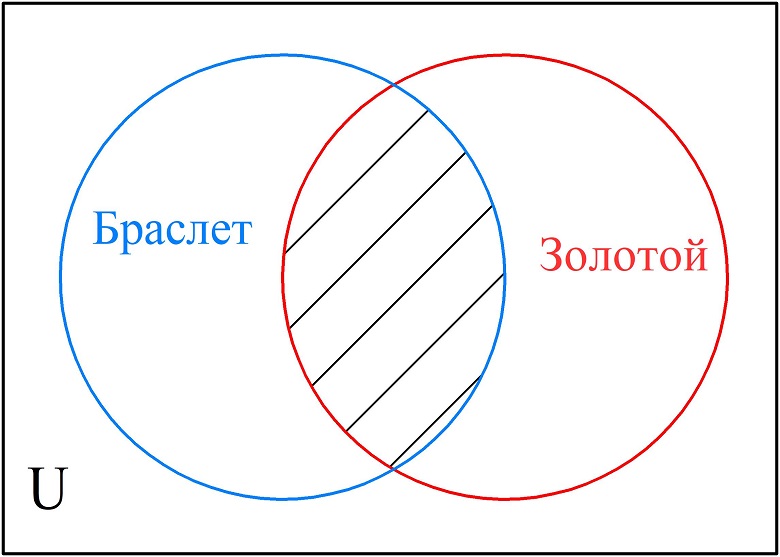
Построим диаграмму для первого запроса. В этом случае будем штриховать область пересечения множества страниц со словом «золотой» и множества страниц со словом «браслет».
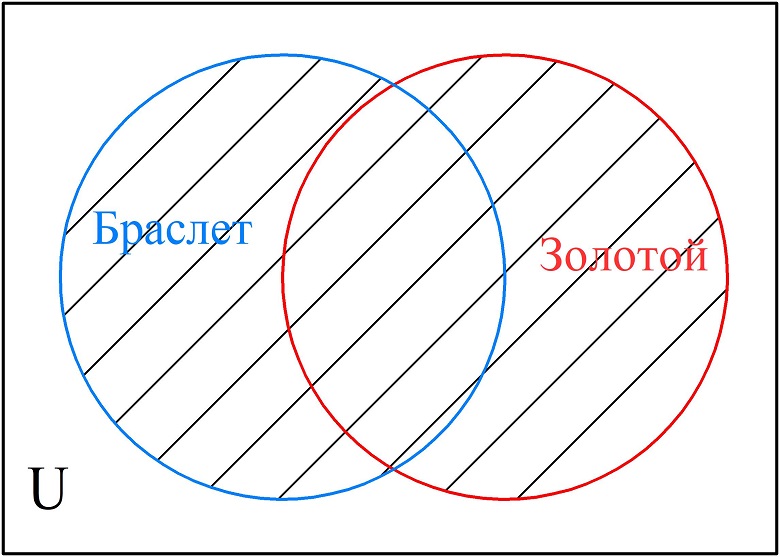
Изобразим на следующей диаграмме второй запрос. Заштрихованной будет область двух множеств.
Заштрихованная область на второй диаграмме больше, чем на первой. Отсюда можно сделать вывод, что количество страниц, выдаваемых поисковиком на второй запрос, будет больше.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так