Определение десятичного логарифма в математике

Что такое lg в математике

Существует особое обозначение данной категории функций: \(\log_{10}x\overset{def}{=}\lg x\)

С таким обозначением можно часто столкнуться при решении примеров на уроках алгебры в школе и при выполнении самостоятельных работ. Запись несколько отличается от стандартного выражения для логарифма. С другой стороны, можно сразу определить, что речь в задании идет именно о десятичном логарифме, который достаточно просто вычислить, применяя его свойства.

Заметим, что основание логарифма равно десяти, что больше по сравнению с единицей. Отсюда можно сделать вывод о принадлежности десятичному логарифму каждого из свойств, характерных для логарифмов, основание которых превышает единицу.  Вместе с тем десятичный логарифм обладает уникальными свойствами, существенно упрощающими процесс решения примеров, в которых они содержатся.

Введем обозначения для компонентов десятичного логарифма:

• целая часть \([\lg x]\)  носит название характеристики;
• дробную часть \(\left\{\lg x\right\}\)называют мантиссой.

В данном случае характеристика представляет собой порядок числа \([\lg с]=n\), в свою очередь, мантиссой является \(\left\{\lg с\right\}=\lg a\).

Свойства десятичных логарифмов

Далее перечислим свойства, характерные для любого десятичного логарифма. Данные соотношения целесообразно использовать в процессе решения задач разной сложности. С их помощью представляется возможным значительно ускорить расчеты. При условии, что х и у больше по сравнению с нулем, являются справедливыми следующие соотношения:

• \(lg х = \log_{10}{х}\)
• \(10^{\lg{b}}=b\)
• \(lg 1 = 0\)
• \(lg 10 = 1\)
• \(lg 10^{n} = n\)
• \(lg (х \cdot у) = lg х + lg у\)
• \(lg ху = lg х – lg н\)
• \(lg х^{n} = n lg х\)
• \((lg х)' = lх ln 10\)
• \(\int lg х dх = х lg х – х ln 10 + С\)
• \(\lim_{х \rightarrow +\infty} lg х = - \infty\)

Вычисление десятичного логарифма

Вспомним, что для обозначения десятичного логарифма используют выражение lg, так как его основание равно десяти. Таким образом, можно записать справедливое равенство:

\(\log_{10} = lg\)

Вычисление десятичного логарифма не вызывает трудностей. Достаточно лишь запомнить простое правило, согласно которому для определения десятичного логарифма требуется его основание в виде 10 возвести в степень х.

Отрицательный десятичный логарифм

Логарифм имеет знак в виде плюса или минуса в зависимости от числа, которое подвергли логарифмированию. Запишем, какие условия справедливы в этом случае:

• когда рассматриваемое число больше по сравнению с единицей, логарифм имеет знак плюс;
• в том случае, когда логарифмируемое число не меньше нуля, но не более единицы, то логарифм является отрицательным.

Разобраться со знаком алгоритма сможет каждый школьник. Однако встречаются в области алгебре такие примеры, с которыми в действительности возникают трудности. Закрепим полученную информацию на практике и запишем наглядный пример того, как определять в формуле знак логарифма.

Примечательно, что для стандартизации действий с десятичными логарифмами было принято решение ставить сверху черту над отрицательными логарифмами. К примеру, подобное действие можно записать в следующей форме:

\(\lg \,0{,}012\approx -2+0{,}079181={\bar {2}}{,}079181\)

Заметим, что мантисса для такого логарифма, которая соответствует табличному значению, в любом случае буде иметь знак плюс.

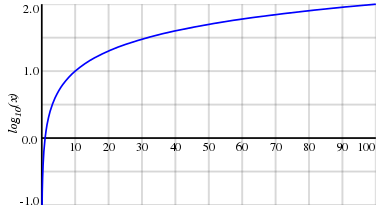
График

Изобразим график, который соответствует десятичному логарифму на координатной плоскости:

 

Источник: ru.wikipedia.org

Примеры

Решение

Заметим, что все логарифмы, записанные в выражениях, являются десятичными, что становится понятно по формату их представления. Таким образом, при решении этой задачи целесообразно воспользоваться свойствами, характерными для десятичного логарифма. Выполним вычисления:

\(\lg x=2\lg a+\lg 7\)

\(\lg x=\lg a^2+\lg 7=\lg(7a^2)\)

\(x=7a^2\)

\(\lg x=2\lg(a+c)-3\lg(a-c)\)

\(\lg x =\lg(a+c)^2-\lg(a-c)^3=\lg\frac{(a+c)^2}{(a-c)^3}\)

\(x=\frac{(a+c)^2}{(a-c)^3}\)

\(\lg x=\frac13\lg 54+\lg 5-\frac13\lg 16\)

\(\lg x=\lg 54^{\frac13}+\lg 5-\lg 16^{\frac13}=\lg\frac{54^{\frac13}\cdot 5}{16^3}= \lg\frac{(27\cdot 2)^{\frac13}\cdot 5}{(2^4)^{\frac13}} = \lg\frac{3\cdot 2^{\frac13}\cdot 5}{2^{\frac43}} = \lg\frac{15}{2} =\lg 7,5\)

\(x=7,5\)

\(\lg x=\lg\sqrt[{3}]{2-\sqrt{3}}+\lg\sqrt[6]{7+4\sqrt{3}}\)

\(\lg\left(\sqrt[{3}]{2-\sqrt{3}}\cdot \sqrt[6]{7+4\sqrt{3}}\right)\)

В данном случае следует выполнить преобразования выражения, которое заключено в скобки. После этого значительно упрощается процесс расчетов:

\(\sqrt[{3}]{2-\sqrt{3}}\cdot \sqrt[6]{7+4\sqrt{3}} = \sqrt[6]{(2-\sqrt{3})^2(7+4\sqrt{3})} = \sqrt[6]{(4-4\sqrt{3}+3)(7+4\sqrt{3})} = \\ =\sqrt[6]{(7-4\sqrt{3})(7+4\sqrt{3})} = \sqrt[6]{7^2-(4\sqrt{3})^2}=\sqrt[6]{49-48}=1\)

\(\lg x=\lg 1\)

\(x=1\)

Ответ: \(x=7a^2, x=\frac{(a+c)^2}{(a-c)^3}, x=7,5, x=1\)

Решение

Основание, которое соответствует десяти, характерно для десятичного логарифма. Зная это, воспользуемся теми свойствами, которые характерны для десятичных логарифмов. В результате получится легко справиться с поставленными задачами.

\(x=\frac{3a^2\sqrt[3]{b^7}}{c^5(a-b)}\)

\(\lg x=\lg\frac{3a^2\sqrt[3]{b^7}}{c^5(a-b)}=\lg 3+\lg a^2+\lg\sqrt[3]{b^7}-\lg c^5-\lg(a-b)=\\ =\lg 3+2\lg a+\frac73\lg b-5\lg c-\lg(a-b)\)

\(x=\frac{\sqrt[3]{100\sqrt{10a\sqrt[4]{0,1a^2}}}}{10\sqrt{0,1a}}\)

\(\lg x=\lg\frac{\sqrt[3]{100\sqrt{10a\sqrt[4]{0,1a^2}}}}{10\sqrt{0,1a}} = \lg\sqrt[3]{100\sqrt{10a\sqrt[4]{0,1a^2}}} - \lg 10\sqrt{0,1a}=\\ =\frac13\lg\left(100\sqrt{10a\sqrt[4]{0,1a^2}}\right)-(\lg 10+\lg\sqrt{0,1a})=\frac13\left(\lg 100+\lg\sqrt{10a\sqrt[4]{0,1a^2}}\right)-\\ -\left(1+\frac12\lg(0,1a)\right)=\frac13\left(2+\frac12\lg(10a\sqrt[4]{0,1a^2})\right)-\left(1+\frac12(\lg 0,1+\lg a)\right)=\\ =\frac23+\frac32\left(\lg 10+\lg a+\lg\sqrt[4]{0,1a^2}\right)-1-\frac12\cdot(-1)-\frac12\lg a=\\ =\left(\frac23+\frac32-1+\frac12\right)+\left(\frac32-\frac12\right)\lg a+\frac32\cdot \frac14(\lg 0,1+\lg a^2)=\\ =\frac53+\lg a+\frac38\cdot(-1)+\frac38\cdot 2\lg a=\left(\frac53-\frac38\right) + \left(1+\frac34\right)\lg a=\frac{31}{24}+\frac74\lg a\)

Важно отметить, что параллельно было сформировано более простая запись выражения:

\(x=10^{\frac{31}{24}}\cdot a^{\frac74}\)

Заметим, что вычисление логарифмов значительно упрощает решение примеров со сложными степенями.

Ответ: \(\lg x=\lg 3+2\lg a+\frac73\lg b-5\lg c-\lg(a-b), \lg x=\frac{31}{24}+\frac74\lg a.\)

 

Решение

Воспользуемся правилом вычисления десятичных логарифмов и запишем последовательные расчеты, чтобы найти ответ:

\(lg 100 = lg 10^{2} = 2\)

\(lg 1000 = lg 10^{3} = 3\)

\(lg 0.1 = lg 10^{-1} = -1\)

\(lg 0.01 = lg 10^{-2} = -2\)

\(lg 0.001 = lg 10^{-3} = -3\)

Ответ: 2, 3, -1, -2, -3.

Решение

Рассмотрим внимательно записанное выше выражение. Заметим, что по условиям задания явно имеет место такое выражение:

\(lg b \cdot lg a = lg a \cdot lg b\)

Далее следует представить число 10 в соответствующих степенях:

\(10^{ lg b \cdot lg a } = 10^{ lg а\cdot lg b}\)

\((10^{ lg b })^{ lg a } = (10^{ lg а })^{ lg b }\)

\(b^{ lg a } = а^{ lg b }\)

Таким образом, путем несложных преобразований удалось доказать справедливость исходного соотношения.

Ответ: равенство является справедливым.