Выборочная дисперсия: формула, как найти
Что такое выборочная дисперсия
Интервальным вариационным рядом называют последовательность распределения с однородными группировками, сформированными в зависимости от признака, который меняется постоянно, либо принимает чрезмерно большое количество значений.
Обобщенный вид рассматриваемого ряда можно представить, как интервалы \(\left.\left[a_{i-1},a_i\right.\right)\):
\(\left.\left[a_{0},a_1\right.\right), \left.\left[a_{1},a_2\right.\right), ... , \left.\left[a_{k-1},a_k\right.\right)\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
с частотами \((f_i)\):
\((f_1\), \(f_2\), ..., \(f_k)\).
В данном случае k обозначает количество интервалов, с помощью которых осуществляется разбивка ряда.
Размах вариации представляет собой протяженность интервала в границах изменений изучаемого параметра:
F = х макс. – х мин.
При решении задач на интервальные ряды с вариациями будет полезно применять правило Стерджеса. С его помощью определяют подходящее количество интервалов k, используя которые целесообразно поделить ряд, собранный из N чисел:
\(k=1+\lfloor \log _{2}N\rfloor \),
\(k=1+\lfloor 3.322\lg N\rfloor\)
Шаг интервальной последовательности с вариациями демонстрирует, как относится вариация с определенным размером к количеству периодов. Результат округляют вверх до некой точности: \(h=\lceil\frac{R}{k}\rceil\)
Сформировать интервальную последовательность можно путем пошагового выполнения следующих действий:
- Входящие данные служат величинами характеристик, то есть \( \left\{x_j\right\},\ j=\overline{1,N}\). В первую очередь следует выяснить, чему равна размерность вариации: \(R=x_{max}-x_{min}.\)
- На втором шаге алгоритма необходимо вычислить оптимальное число интервалов:\( k=1+\lfloor\log_2 N\rfloor\).
- Затем можно определить шаг последовательности, то есть \( h=\left\lceil\frac{R}{k}\right\rceil\).
- Вычислить узлы последовательности: \(a_0=x_{min},\ \ a_i=1_0+ih,\ \ i=\overline{1,k}\).
- Рассчитать, чему равны частоты \(м\) по формуле \(\left.\left[a_{i-1},a_i\right.\right)\).
Таким образом, получается интервальная последовательность с определенными периодами:
\(\left.\left[a_{i-1},a_i\right.\right)\)
Частоты в нем соответствуют:
\(f_i,\ i=\overline{1,k}\)
Важно обратить внимание на наличие округления вверх у шага h. По этой причине крайний узел составляет:
\(a_k\geq x_{max}\)
В качестве примера рассмотрим ситуацию, при которой у какого-то количества учащихся измеряли рост. Всего было проведено 100 замеров. По итогам мероприятия удалось выяснить, что самый маленький показатель составляет 142 см, а максимальный рост равен 197 см. Попробуем вычислить узлы, чтобы образовать интервальную последовательность:
\(N=100,\ x_{min}=142\ см,\ x_{max}=197\ см.\)
\(R=197-142=55\)
\(k=1+\lfloor 3,322\cdot\lg 100\rfloor=1+\lfloor 6,644\rfloor=1+6=7\)
\(h=\lceil\frac{55}{5}\rceil=\lceil 7,85\rceil=8\)
В результате, получили следующие рядовые узлы:
\(a_0=x_{min}=142,\ a_i=142+i\cdot 8,\ i=\overline{1,7}\)
Относительная частота интервала, имеющего вид \(\left.\left[a_{i-1},a_i\right.\right)\), является отношением частоты \((f_i)\) к суммарному числу исходов, то есть: \(w_i=\frac{f_i}{N},\ i=\overline{1,k}\)
Гистограмма относительных частот интервального ряда имеет вид фигуры, в состав которой входят прямоугольники с шириной, равной рядовому шагу, и высотой, соответствующей относительным частотам всех интервалов
.Заметим, что величина площади гистограммы соответствует единице, учитывая точность до округлений. Таким образом, сформулирована эмпирическая закономерность распределения изучаемого признака.
Если продолжать рассматривать первый пример, в котором производился замер роста учеников, то можно составить эмпирическую функцию распределения по отношению к серединам интервалов:
\(F(x)= \begin{cases} 0,\ x\leq 146\\ 0,04,\ 146\lt x\leq 154\\ 0,11,\ 154\lt x\leq 162\\ 0,22,\ 162\lt x\leq 170\\ 0,56,\ 170\lt x\leq 178\\ 0,89,\ 178\lt x\leq 186\\ 0,97,\ 186\lt x\leq 194\\ 1,\ x\gt 194 \end{cases}\).
Выборочной средней для интервального ряда называют среднюю взвешенную относительно частот, то есть:
\(X_{cp}=\frac{x_1f_1+x_2f_2+...+x_kf_k}{N}=\frac1N\sum_{i=1}^k x_if_i\)
Здесь x_i определяет середины интервалов, то есть:
\(x_i=\frac{a_{i-1}+a_i}{2},\ i=\overline{1,k}\)
Другой вариант формулы:
\(X_{cp}=\sum_{i=1}^k x_iw_i\)
Модальный интервал представляет собой такой интервал, который имеет самую большую частоту:
\( f_m=max f_i\)
Определение моды в случае интервального вариационного ряда подразумевает выполнение расчетов с помощью следующего соотношения:
\(M_o=x_o+\frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h\)
В данном случае \(h\) является шагом интервального ряда, \(x_o\) определяет границу внизу, \(f_m,f_{m-1},f_{m+1}\) представляют собой частоты модального интервала, интервала с левой стороны от модального и интервала с правой стороны.
Медианный интервал является первым по счету интервалом с левой стороны, характеризующимся превышением кумулятой значения 0,5.
Вычислить медиану представляется возможным с использованием следующего справедливого равенства:
\(M_e=x_o+\frac{0,5-S_{me-1}}{w_{me}}h\)
Здесь \(h\) обозначает шаг, \(x_o\) определяет границу снизу, \(S_{me-1}\) является накопленной относительной частотой для интервала, который расположен в левой стороне по отношению к медианному, \(w_{me}\) представляет собой относительную частоту медианного интервала.
Выборочной дисперсией для последовательности с вариациями называют усредненную для квадрата отклонения от средней: \(D=\frac1N\sum_{i=1}^k(x_i-X_{cp})^2 f_i=\frac1N\sum_{i=1}^k x_i^2 f_i-X_{cp}^2\)
В данном случае \(x_i \) определяет середины интервалов:
\(x_i=\frac{a_{i-1}+a_i}{2},\ i=\overline{1,k}\)
Другой вариант записи формулы:
\(D=\sum_{i=1}^k(x_i-X_{cp})^2 w_i=\sum_{i=1}^k x_i^2 w_i-X_{cp}^2\)
Выбранное в среднем квадратичное изменение вычисляют в виде корня второй степени из выборочной дисперсии: \(\sigma=\sqrt{D}\)
Исправленная выборочная дисперсия
Вычислить исправленную выборочную дисперсию можно с помощью следующего соотношения:
\(S^2=\frac{N}{N-1}D\)
Нормальное отклонение выборки представляет собой значение в виде корня второй степени, извлеченного из исправленной выборочной дисперсии, то есть: \(s=\sqrt{S^2}\)
Коэффициентом вариации называют соотношение нормального отклонения выборки и выборочной усредненной, которое определено в процентах, то есть: \(V=\frac{s}{X_{cp}}\cdot 100\text{%}\)
Генеральная дисперсия
Допустим, что Х обозначает какую-то произвольную величину. Представим, что имеется некоторая генеральная совокупность с учетом данной величины Х. Сформулируем на основании этих данных определения.
Генеральная совокупность представляет собой набор произвольно выбранных элементов определенного вида, которые являются объектами изучения для выявления конкретизированных значений произвольной величины. Наблюдательный процесс за одной случайной Х определенного вида предполагает стабильные условия.
Генеральная дисперсия является средним арифметическим квадратов изменений значений вариант генеральной совокупности по сравнению с их усредненным значением.
Предположим, что варианты обладают следующими значениями:
\(x_1,\ x_2,\dots ,x_k\)
Частоты при этом составляют:
\(n_1,\ n_2,\dots ,n_k\)
В таком случае можно вычислить, чему равна генеральная дисперсия с помощью справедливого равенства:
\(D г = (\sum_i^ N (Xi-\overline{Xг})^{2}/N\)
При разнообразных вариантах Х формула примет следующий вид:
\(D г = (\sum_i^n (Ni (Xi-\overline{Xг})) ^{2}/N\)
Заметим, что в данном случае генеральное среднее квадратическое изменение можно определить в виде корня второй степени, извлеченного из генеральной дисперсии:
\({\sigma }_г=\sqrt{D_г}\)
Свойства выборочной дисперсии
Рассмотрим ключевые свойства, которые характерны для выборочной дисперсии:
- Данная дисперсия представляет собой дисперсию выборочного распределения в теории. К примеру, представим \({\hat {F}}(x)\) в виде выборочной функции распределения рассматриваемой выборки. В таком случае при каком-либо неизменном \omega \in \Omega функция \({\hat {F}}(\omega ,x)\) представляет собой функцию, не являющуюся случайной, дискретного распределения. Дисперсия для такого распределения вычисляется следующим образом: \(S_{n}^{2}(\omega )\).
- Пара выборочных дисперсий представляет собой объективные оценки дисперсии с точки зрения теории. В том случае, когда \({\mathrm {D}}[X_{i}]=\sigma ^{2}<\infty\), имеем, что \(S_{n}^{2}\to ^{{\!\!\!\!\!\!{\mathbb {P}}}}\;\sigma ^{2}\), а также \(S^{2}\to ^{{\!\!\!\!\!\!{\mathbb {P}}}}\;\sigma ^{2}\). Заметим, что знак \(«\to ^{{\!\!\!\!\!\!{\mathbb {P}}}}»\) показывает, что относительно вероятности присутствует сходимость.
- Выборочная дисперсия представляет собой оценку со смещением относительно дисперсии в теории. Наряду с этим фактом, заметим, что исправленная выборочная дисперсия подразумевает не смещенную оценку, то есть: \({\mathbb {E}}\left[S_{n}^{2}\right]={\frac {n-1}{n}}\sigma ^{2}\), а также \({\mathbb {E}}\left[S^{2}\right]=\sigma ^{2}\).
- Выборочная дисперсия классического распределения обладает распределением хи-квадрат. Представим, что соблюдено следующее условие \(X_{i}\sim {\mathrm {N}}(\mu ,\sigma ^{2}),\;i=1,2,\ldots\) . В таком случае справедливым является такое соотношение: \((n-1){\frac {S^{2}}{\sigma ^{2}}}\equiv n{\frac {S_{n}^{2}}{\sigma ^{2}}}\sim \chi ^{2}(n-1).\)
Для чего применяется
Применение выборочной дисперсии оправдано с точки зрения удобства и эффективности проведения наблюдений. К примеру, когда необходимо рассмотреть количественную характеристику генеральной совокупности, используют этот метод. Предположим, что по результатам анализа теоретических данных было определено конкретное распределение для признака. Формируется необходимость оценить параметры, характерные для рассматриваемого распределения.
В распространенных случаях специалист, осуществляющий исследования, может получить информацию по выборкам, сформированным по итогам какого-то количества наблюдений. С помощью этих данных представляется возможным определить признак для оценки. При изучении количественной величины с учетом ее независимости предполагается оценка неизвестного параметра с точки зрения статистики по распределению в теории. Таким образом, требуется определить функцию от изучаемых произвольных параметров, демонстрирующую примерное значение характеристики. Рассмотрим несколько примеров
Арендаторы офисных помещений в бизнес-центре имеют разный возраст. Согласно опросу 30 человек, были получены следующие результаты:
18, 38, 28, 29, 26, 38, 34, 22, 28, 30, 22, 23, 35, 33, 27, 24, 30, 32, 28, 25, 29, 26, 31, 24, 29, 27, 32, 24, 29, 29
Требуется изучить интервальный ряд.
Решение
Запишем исходные данные:
\(x_{min}=18,\ \ x_{max}=38,\ \ N=30\)
Величина размаха вариации соответствует следующему значению:
\(R=38-18=20\)
Подходящим количеством интервалов является следующее значение:
\(k=1+\lfloor\log_2 30\rfloor=1+4=5\)
Интервальный ряд обладает шагом, который удобно вычислить по формуле:
\(h=\lceil\frac{20}{5}\rceil=4\)
Запишем полученные рядовые узлы:
\(a_0=x_{min}=18,\ \ a_i=18+i\cdot 4,\ \ i=\overline{1,5}\)
Перечислим характерные интервалы \( \left.\left[a_{i-1},a_i\right.\right)\) лет:
\(\left.\left[18;22\right.\right), \left.\left[22;26\right.\right), \left.\left[26;30\right.\right), \left.\left[30;34\right.\right), \left.\left[34;38\right.\right).\)
Определим, чему равны частоты для всех интервалов:
\(1, 7, 12, 6, 4\)
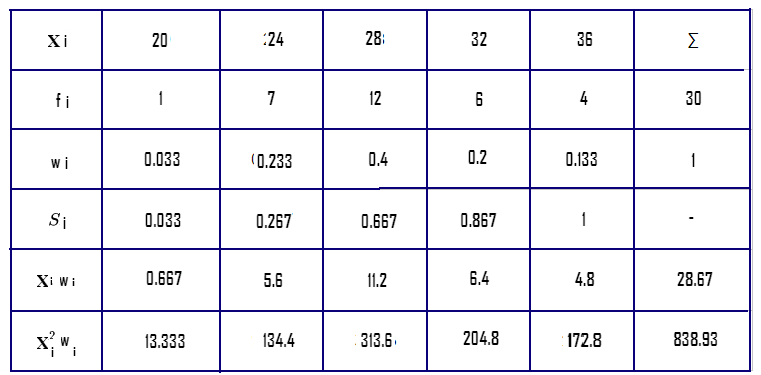
Таблица для проведения расчетов:
Вычислим, чему равна эмпирическая функция распределения при таких условиях:
\(F(x)= \begin{cases} 0,\ x\leq 20\\ 0,033,\ 20\lt x\leq 24\\ 0,267,\ 24\lt x\leq 28\\ 0,667,\ 28\lt x\leq 32\\ 0,867,\ 32\lt x\leq 36\\ 1,\ x\gt 36 \end{cases}\)
Рассчитаем остальные характеристики:
\(X_{cp}=\sum_{i=1}^k x_iw_i\approx 28,7\ \text{(лет)}\)
\(x_0=26,\ f_m=12,\ f_{m-1}=7,\ f_{m+1}=6,\ h=4\\ M_o=x_o+\frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\\ =26+\frac{12-7}{(12-7)+(12-6)}\cdot 4\approx 27,8\ \text{(лет)}\)
\(x_0=26,\ w_m=0,4,\ S_{me-1}=0,267,\ h=4\\ M_e=x_o+\frac{0,5-S_{me-1}}{w_{me}}h=26+\frac{0,5-0,4}{0,267}\cdot 4\approx 28,3\ \text{(лет)}\)
\(X_{cp}=28,7;\ M_o=27,8;\ M_e=28,6\\ X_{cp}\gt M_e\gt M_0\)
В результате сформировался ряд, имеющий асимметрию справа. Можно отметить высокую степень асимметричности:
\(\frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =\frac{0,9}{0,1}=9\gt 3\)
Вычислим, чему равна выборочная дисперсия и СКО:
\(D=\sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2\approx 17,2\\ \sigma=\sqrt{D}\approx 4,1\)
В таком случае исправленная выборочная дисперсия определена следующим значением:
\(S^2=\frac{N}{N-1}D=\frac{30}{29}\cdot 17,2\approx 17,7\)
Рассчитаем величину стандартного отклонения:
\(s=\sqrt{S^2}\approx 4,2\)
Выполним расчет коэффициента вариации:
\(V=\frac{4,2}{28,7}\cdot 100\text{%}\approx 14,7\text{%}\lt 33\text{%}\)
Можно сделать вывод об однородности рассматриваемой выборки. Усредненное значение возраста арендаторов составляет:
\(X_{cp}=28,7\)
Данное значение допустимо применить ко всей генеральной совокупности.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так