Определение вписанного угла
Вписанные углы — это
Вписанным называют такой угол, вершина которого расположена на окружности, а стороны имеют общие точки с рассматриваемой окружностью.
При построении вписанного угла роль опоры играет дуга, представляющая собой часть окружности, либо хорда, с помощью которой соединены оконечные точки дуги. Справедливо утверждение об образовании вписанного угла с помощью пары хорд, а также посредством хорды и касательной, обладающих общими точками пересечения во внутреннем пространстве окружности.
Допустимы разные варианты представления вписанного угла:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- остроугольный;
- прямой;
- тупоугольный.
Градусная мера вписанного угла зависит от расположения его сторон по отношению к центральной точке окружности. Этот параметр соответствует интервалу от 0° до 180°. Изучаемый геометрический объект имеет характерные свойства, с помощью которых можно упростить решение различных задач.
Свойства
Существует ряд особенностей и признаков, которыми обладает произвольный вписанный угол. Такие закономерности позволяют оперативно и точно вычислять параметры углов и других характеристик в геометрии. Перечислим основные положения:
- градусная мера вписанного угла в два раза меньше по сравнению с величиной центрального угла при условии, что данные объекты обладают общей опорной дугой;
- углы, которые вписаны в некоторую окружность и опираются на одинаковую дугу, характеризуются идентичными градусными мерами;
- если вписанный угол опирается на диаметр, то величина такого угла соответствует 90°.
Теорема о вписанном угле
Величина вписанного угла составляет \(\frac{1}{2}\) часть от меры центрального угла, имеющего с ним общую опорную дугу, и дополняет до 180° половину центрального угла, опирающегося на дополнительную дугу. При любом варианте построения из озвученных примеров вписанный угол находят как половину дуги, которая играет роль опоры для рассматриваемого угла.
Предусмотрено несколько следствий, вытекающих из описанного выше теоретического заключения:
- если углы являются вписанными в окружность и опираются на одинаковую ее дугу, то такие углы обладают равными градусными мерами;
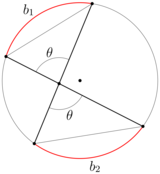
- величину вертикальных углов, сформированных пересекающимися отрезками, перекрестно совмещающих конечные точки пары хорд, не имеющих общих точек пересечения, определяют как половину суммы угловых мер стягиваемых хордами дуг, или дополняют это значение до 180°.
Источник: ru.wikipedia.org
Исследуемую теорему, определяющую параметры вписанных углов, применяют на практике в процессе решения заданий по геометрии. Такой подход называют методом вспомогательной окружности. Смысл озвученного принципа заключается в определении параметров многоугольников с четырьмя углами, вписанных в окружность, для вычисления в последующем искомых угловых величин. При этом обращаются к теоретической закономерности и ее следствиям.
Как найти: формулы
Представим, что \(\angle ВАС\) вписан в некоторую окружность, центральная точка которой обозначена за О и расположен на отрезке АВ. В таком случае целесообразно использовать следующую формулу для определения величины вписанного угла:
\(\angle ВОС = 2 \cdot \angle ВАС\)
Следующее уравнение, с помощью которого допустимо рассчитывать градусную меру вписанного угла, построено на основании его соотношения с дугой окружности, расположенной во внутреннем пространстве рассматриваемого угла. Стороны вписанного угла высекают данную дугу, а его величина соответствует половине ее градусной меры:
\(\angle ВАС = \frac{1}{2} \smile ВС\)
Примеры решения задач
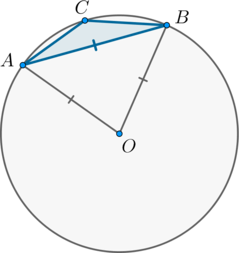
В треугольнике АВС один угол больше 90°, а сторона АВ по величине соответствует радиусу окружности, описанной вокруг рассматриваемой треугольной фигуры. Требуется вычислить градусную меру тупого угла С.
Источник: oge.shkolkovo.net
Решение
На рисунке по условиям задания отмечена центральная точка О. Заметим, что АО = ОВ. Рассматриваемые отрезки совпадают с радиусом построенной окружности. С помощью этих линий образован \(\triangle АОВ\). На основании сделанных выводов данная геометрическая фигура представляет собой равносторонний треугольник. Исходя из равенства углов, которые в сумме составляют 180°, получим что:
\(\angle АОВ = 60°\)
Дуга, служащая опорой для рассматриваемого угла, характеризуется аналогичной величиной:
\(\smile АВ = 60°\)
Полученный результат позволяет вычислить угловую меру большей по размеру дуги АВ:
360° - 60° = 300°
Заметим, что на изображении представлен \(\angle АСВ\), который является вписанным в окружность. Этот угол опирается на дугу АВ, обладающую большим размером. Исходя из теоремы о вписанном угле, составим следующее уравнение и запишем искомый ответ:
\(\angle АСВ = \frac{1}{2} \cdot \smile АВ = \frac{1}{2} \cdot 300° = 150°\)
Ответ: 150°.
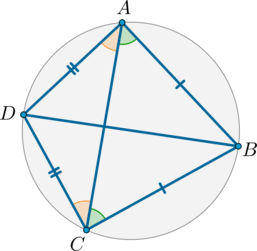
На рисунке изображена окружность. На границах этой геометрической фигуры последовательно отметили две пары точек АВСD. Требуется вычислить, чему соответствует градусная мера угла \(\angle BAD\) , если соблюдено следующее условие:
АВ = ВС
CD = DA
Источник: oge.shkolkovo.net
Решение
В первую очередь необходимо проанализировать геометрическую фигуру и ее элементы, изображенные на рисунке выше. Заметим, что треугольники ВАС и DАС являются равнобедренными.
Из этого утверждения допустимо сделать вывод о справедливости следующих соотношений:
\(\angle ВАС = \angle ВСА\)
\(\angle DAC = \angle DCA\)
Исходя из сделанного вывода, можно на втором этапе прийти к логичному заключению о равенстве углов:
\(\angle A = \angle C\)
Указанные углы вписаны в окружность. В таком случае в сумме вписанные углы составляют половину от суммы дуг, на которые они опираются. Сформулируем сделанное заключение в виде математического соотношения:
\(\angle A + \angle C = \frac{1}{2}(\smile DCB +\smile DAB)\)
Так как угловая мера записанных в выражении дуг составляет 360°, при суммировании углов \(\angle A и \angle C\) получается величина в 180°. Учитывая равенство рассматриваемых углов, несложно посчитать искомый ответ:
\(\angle A = \angle C = 90°\)
Ответ: 90°.
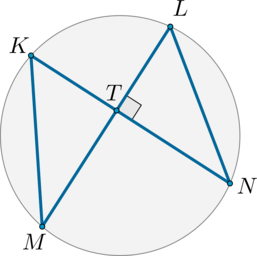
Имеется пара взаимно перпендикулярных хорд, обозначенных за KN и LM. Величина угла \(\angle KML\), образованного этими линиями, составляет 35°. Требуется вычислить градусную меру \(\angle NLM\) .
Источник: oge.shkolkovo.net
Решение
Проанализируем изображение, составленное по условиям задания. Заметим, что по определению \(\angle KML и \angle KNL\) являются вписанными. Идентифицированные таким образом углы опираются на одинаковую дугу, что говорит о равенстве их величин. Запишем равенство, выходящее из сделанного вывода:
\(\angle KNL = 35°\)
Исходя из представленного утверждения, несложно вычислить градусную меру искомого угла:
\(\angle NLM = 180° - 90° - 35° = 55°\)
Ответ: 55°.
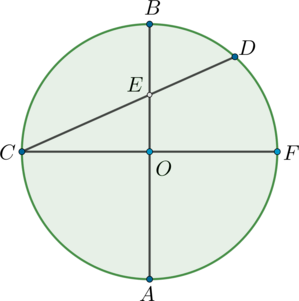
Дана некоторая окружность с центром в точке О и диаметром АВ, пересекающим хорду CD в отметке Е. Образованная дуга АС соответствует 90°. Дуга СBD составляет 150°. Требуется вычислить градусную меру угла \(\angle СЕА\).
Источник: oge.shkolkovo.net
Решение
В заданной окружности проведем диаметр CF. Так как точка О является центральной, \(\angle СОА\) составляет 90°. Запишем соответствующее математическое соотношение:
\(\angle СЕА = 90° - \angle DCF\)
Рассмотрим дугу \(\smile СВD\). Градусная мера этого элемента составляет 150°. Заметим, что отрезок CF играет роль диаметра. В таком случае:
\(\smile DF = 180° - 150° = 30°\)
Из теоретического курса геометрии известно, что вписанный угол по величине составляет половину от дуги, которая служит его опорой. Руководствуясь данным утверждением, выполним следующие вычисления:
\(\angle DCF = \frac{1}{2} \cdot 30° = 15°\)
На заключительном шаге остается рассчитать градусную меру искомого угла:
\(\angle СЕА = 90° - 15° = 75°\)
Ответ: 75°.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так