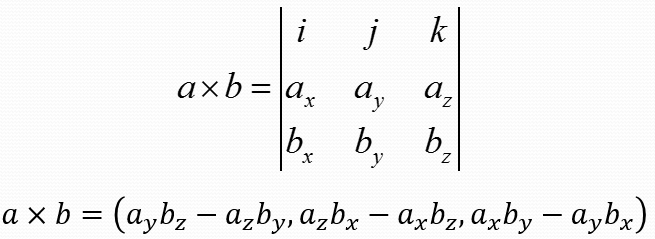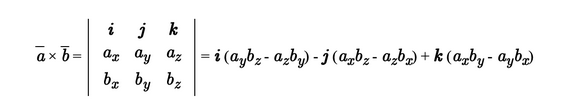Что нужно знать об углах между векторами — основные сведения

Содержание:

Содержание

Определение (понятие) угла между векторами

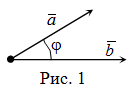
Угол между двумя векторами \(\overrightarrow{a}\) и \(\overrightarrow{b}\), которые обладают единым началом — самый маленький угол, на который необходимо совершить переворот одного из векторов вокруг точки приложения до положения, когда вектор примет такое же направление, как у другого вектора.

Как на рисунке ниже:

Длина вектора, а также угол между векторами являются терминами часто применимыми в науки, а для человека понятными на интуитивном уровне при определении вектора в качестве отрезка с конкретным направлением.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

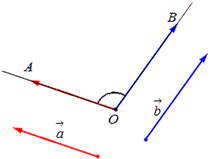
Для того, чтобы понять, что такое угол между векторами воспользуемся примерами. Зададим на конкретной плоскости или же в трехмерном пространстве два вектора \(\overrightarrow{a}\)и \(\overrightarrow{b}\). Определим сразу, что они не являются нулевыми. Далее нужно задать произвольную точку O, а уже от нее отложить векторы \(\overrightarrow{OA}=\overrightarrow{b}\) и \(\overrightarrow{OB}=\overrightarrow{b}\).

Примечание 1

Вектор — нормальная прямая, которая имеет величину и направление.

Угол между векторами — угол, который образовался между лучами OA и OB. Угол, который получился в примере нужно обозначать таким образом: \(\overbrace{\overrightarrow{a}\overrightarrow{b}}\).

Интуитивно понятно, что угол обладает способность принимать любые значения от 0 до \(\pi\) или от 0 до 180 градусов.

Векторы считаются сонаправленными тогда, когда \((\overbrace{\overrightarrow{a}\overrightarrow{b}})=0\). А противоположно направленными считаются в случае, когда \( (\overbrace{\overrightarrow{a}\overrightarrow{b}})=\pi\).

Перпендикулярными векторы считаются в случае, когда угол между ними равняется 90 градусов или же \(\frac{\pi}{2}\) радиан. Если один из векторов не является нулевым, тогда угол \(\overbrace{\overrightarrow{a}\overrightarrow{b}}\) является неопределенным.

Примечание 2

Базисным вектором называют векторы базиса, то есть упорядоченный набор единичных векторов в пространстве, такой, что любой вектор из набора может использоваться в виде единственной линейной комбинации векторов данного набора. Ось проекции — скалярная величина, которая равна длине геометрической проекции вектора, если направление и оси и проекции совпадают.

Формула вычисления угла между векторами

По собственному определению угол между двумя векторами находится в промежутке \([0^{\circ}; 180^{\circ}].\) Угол между векторами \(\overrightarrow{a}\) и \(\overrightarrow{b}\) обычно обозначают таким образом: \(\overbrace{\overrightarrow{a}\overrightarrow{b}}\).

Если векторы лежат перпендикулярно друг другу, то угол между такими векторами будет равен \([90^{\circ}]\). Если характер движения векторов — сонаправленные — особенно, если один\оба являются нулевыми, тогда угол между ними будет \([0^{\circ}]\). Если векторы направлены противоположно друг к другу, тогда угол между ними \([180^{\circ}]\). Угол между двумя ненулевыми векторами вычисляется при помощи скалярного произведения.

Так вычислить скалярное произведение можно при помощи длин векторов, помноженных на косинус угла между ними.

Существует общая формула для вычисления угла между векторами:

Формула 1

\(\phi=\arccos(\cos\phi)\)

Определение скалярного произведения векторов

Скалярное произведение двух векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) в итоге даст скалярную величину, равную сумме последовательного произведения координат векторов \(\overrightarrow{a}\)и \(\overrightarrow{b}.\)

Существует два варианта формулировки термина «скалярное произведение».

Формулировка с точки зрения геометрии. Скалярное произведение векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) — скалярная величина, которая равна умножению двух модулей данных векторов, произведение модулей умножено на косинус угла между векторами: \(\overrightarrow{a}\times\overrightarrow{b}=\mid\overrightarrow{a}\mid\times\mid\overrightarrow{b}\mid\times\cos\alpha\).
Формулировка с точки зрения алгебры. Скалярное произведение \(\overrightarrow{a}\) и \(\overrightarrow{b}\) — сумма последовательного умножения координат векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\).

Свойства скалярного произведения векторов

Существует несколько свойств скалярного произведения векторов:

Скалярное произведения вектора самого на себя будет больше или же равно нулю. В итоге получится нуль, если вектор будет равен нулевому вектору.\( \overrightarrow{a}\times\overrightarrow{a}>0\) и \(\overrightarrow{0}\times\overrightarrow{0}=0\).
Скалярное произведение вектора на себя будет равняться квадрату модуля вектора: \(\overrightarrow{a}\times\overrightarrow{a}=\mid\overrightarrow{a}\mid^{2}\).
Можно говорить о коммуникативном характере скалярного произведения, потому что действие скалярного произведение полностью совпадает с переместительным законом: \(\overrightarrow{a}\times\overrightarrow{a}=\overrightarrow{b}\times\overrightarrow{a}\).
Действие скалярного произведения носит дистрибутивный характер, потому что совпадает с распределительным законом: \((\overrightarrow{a}+\overrightarrow{b})\times\overrightarrow{с}=\overrightarrow{a}\times\overrightarrow{с}+\overrightarrow{b}\times\overrightarrow{с}\).
Справедливым для скалярного произведения можно считать и сочетательный закон: \((\overrightarrow{k}\times\overrightarrow{a})\times\overrightarrow{b}=\overrightarrow{k}\times(\overrightarrow{a}\times\overrightarrow{b}\).
Можно говорить об ортогональности (перпендикулярности) двух ненулевых векторов, если их скалярное произведение равно нулю: \(\overrightarrow{a}\neq{0}, \overrightarrow{b}\neq{0},\overrightarrow{a}\times\overrightarrow{b}=0\Leftrightarrow\overrightarrow{a}\perp\overrightarrow{b}.\)

Данные свойства просто обосновываются при помощи дефиниции термина «скалярное произведение» в рамках координатной системы, а также при помощи свойств действий сложения\умножения действительных чисел.

Нахождение угла между векторами с помощью скалярного произведения

Скалярное произведение двух векторов — число или скаляр, которое равно произведению длин двух векторов с косинусом угла между этими векторами.

Если перевести слова на язык знаков, тогда получится, что скалярное произведение двух векторов: \( \overrightarrow{a}\overrightarrow{b}=\mid{\overrightarrow{a}}\mid\mid\overrightarrow{b}\mid\cos<(\overrightarrow{a},\overrightarrow{b})\).

Кроме непосредственно определения выше можно использовать такую теорему для нахождения значения скалярного произведения:

Теорема

Скалярное произведение двух векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) с координатами \(\overrightarrow{a}=(a_{1},a_{2},a_{3})\) и \(\overrightarrow{b}=(b_{1},b_{2},b_{3}\) будет равно сумме произведений конкретных координат.

Представим математически: \(\overrightarrow{a}\times\overrightarrow{b}=a_{1}\times{b_{1}}+a_{2}\times{b_{2}}+a_{3}\times{b_{3}}\).

Скалярное произведение обычно обозначается таким образом: \(\overrightarrow{a}\times\overrightarrow{b}\).

При помощи скалярного произведения возможно найти косинус угла между векторами. Разберем на примерах. Представим, что нам дали векторы \(\overrightarrow{a}\) и \(\overrightarrow{b}\) с координатами \(\overrightarrow{a}=(a_{1},a_{2},a_{3})\) и \(\overrightarrow{b}=(b_{1},b_{2},b_{3}\). Получится, что \(\cos<(\overrightarrow{a}\overrightarrow{b})=\frac{\overrightarrow{a}\overrightarrow{b}}{\mid\overrightarrow{a}\mid\mid\overrightarrow{b}\mid}.\)

Исходя из теоремы получаем, что \(\overrightarrow{a}\times\overrightarrow{b}=a_{1}\times{b_{1}}+a_{2}\times{b_{2}}+a_{3}\times{b_{3}}\). Значит \(\cos\overbrace{\overrightarrow{a}\overrightarrow{b}}==\frac{a_{1}\times{b_{1}}+a_{2}\times{b_{2}}+a_{3}\times{b_{3}}}{\mid{a}\mid\mid{b}\mid}\). Получаем:

\(\cos\overbrace{\overrightarrow{a}\overrightarrow{b}}=\frac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}\sqrt{{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}}\).

При помощи значения косинуса просто найти величину угла.

Нахождение угла между векторами при помощи векторного произведения

Векторное произведение двух векторов — определенный вектор, перпендикулярный двум векторами, чья длина равна произведению длин данных векторов с синусом угла между этими векторами. Вектор и два остальных вектора будет иметь такое же направление, как и декартова система координат.

Обозначают обычно векторное произведение так: \(\overrightarrow{a}x\overrightarrow{b}\).

В математической форме будет так:

\(\mid\overrightarrow{a}x\overrightarrow{b}\mid=\mid\overrightarrow{a}\mid\mid\overrightarrow{b}\mid\sin<(\overrightarrow{a},\overrightarrow{b}).\)
\(\overrightarrow{a}x\overrightarrow{b}\perp\overrightarrow{a},\overrightarrow{a}x\overrightarrow{b}\perp\overrightarrow{b}.\)
\((\overrightarrow{a}\times\overrightarrow{b},\overrightarrow{a},\overrightarrow{b})\) и \((\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})\) являются ориентированными.

Для нахождения вектора векторного произведения можно использовать эту формулу:

Расчет угла между векторами в прямоугольной системе координат

Бывает такой тип задач, в которых векторы задаются при помощи координат в прямоугольном типе системы координат на плоскости\в пространстве. В данном случае найти угол между векторами можно при помощи трансформированной следующей формулы:

Формула 2

\(\cos(\overrightarrow{a}\overrightarrow{b})=\frac{\overrightarrow{a}\overrightarrow{b}}{\mid\overrightarrow{a}\mid\times\mid\overrightarrow{b}\mid}\)

Давайте получим эту формулу в координатной форме.

Длина вектора — квадратный корень от суммы квадратов координат, а скалярное произведение векторов — сумма произведений определенных координат. Значит, формула для вычисления косинуса угла между векторами \(\overrightarrow{a}=(a_{x}, a_{y})\) и \(\overrightarrow{b}=(b_{x}, b_{y})\) на плоскости примет такой вид:

\(\cos\overbrace{\overrightarrow{a}\overrightarrow{b}}=\frac{a_{x}b_{x}+a_{y}b_{y}}{\sqrt{a_{x}^{2}+a_{y}^{2}}\sqrt{{b_{z}^{2}+b_{y}^{2}}}}\)

Для вектора в трехмерном пространстве \(\overrightarrow{a}=(a_{x}, a_{y},a_{z})\) и \(\overrightarrow{b}=(b_{x}, b_{y},b_{z})\) формула будет такой:

Формула 3

\(\cos\overbrace{\overrightarrow{a}\overrightarrow{b}}=\frac{a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}}{\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}\sqrt{{b_{z}^{2}+b_{y}^{2}+b_{z}^{2}}}}\).

Пример 2

Нужно найти угол между векторами \(\overrightarrow{a}=(2,0,-1)\) и \(\overrightarrow{b}=(1,2,3)\). Они заданы в прямоугольной системе координат.

Решение.

Применим формулу

\(\cos\overbrace{\overrightarrow{a}\overrightarrow{b}}=\frac{a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}}{\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}\sqrt{{b_{z}^{2}+b_{y}^{2}+b_{z}^{2}}}}\).

\(\cos\overbrace{\overrightarrow{a}\overrightarrow{b}}=\frac{2\times1+0\times2+(-1)\times3}{\sqrt{2^{2}+0^{2}+(-1)^2}\times\sqrt{1^{2}+2^{2}+3^{2}}}=-\frac{1}{\sqrt{70}}\Rightarrow(\overbrace{\overrightarrow{a}\overrightarrow{b}})=\arccos(-\frac{1}{\sqrt{70}})=-\arccos\frac{1}{\sqrt{70}}\)

Для того, чтобы найти косинус угла можно использовать эту формулу:

\(\cos(\overrightarrow{a}\overrightarrow{b})=\frac{\overrightarrow{a}\overrightarrow{b}}{\mid\overrightarrow{a}\mid\times\mid\overrightarrow{b}\mid}\). Вычислим перед этим длину каждого вектора, а также скалярное произведение:

\(\mid\overrightarrow{a}\mid=\sqrt{2^{2}+0^{2}+(-1)^{2}}=\sqrt{5}\)

\(\mid\overrightarrow{b}\mid=\sqrt{1^{2}+2^{2}+3^{2}}=\sqrt{14}\)

\((\overrightarrow{a}\overrightarrow{b})=2\times1+0\times2+(-1)\times3=-1\)

\(\cos(\overrightarrow{a}\overrightarrow{b})=\frac{\overrightarrow{a}\overrightarrow{b}}{\mid\overrightarrow{a}\mid\times\mid\overrightarrow{b}\mid}=\frac{-1}{\sqrt{5}\times\sqrt{14}}=-\frac{1}{\sqrt{70}}.\)

\(\overbrace{\overrightarrow{a}\overrightarrow{b}}=-\arccos\frac{1}{\sqrt{70}}\)

Ответ: \(\overbrace{\overrightarrow{a}\overrightarrow{b}}=-\arccos\frac{1}{\sqrt{70}}.\)

Формулы скалярного произведения векторов в координатах

Найти скалярное произведение возможно при помощи координат векторов в определенной плоскости или пространстве.

Скалярное произведение двух векторов на плоскости или же в рамках трехмерного пространстве в прямоугольном типе системы координат находится при помощи перемножении конкретных координат векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\).

Получается, что у векторов \(\overrightarrow{a}=(a_{x};a_{y)}\) и \(\overrightarrow{b}=(b_{x};b_{y)}\) в плоскости декартовой (прямоугольной) системе координат будет следующая формула для нахождения скалярного произведения: \(\overrightarrow{a}\overrightarrow{b}=(a_{x}\times{b_{x}}+a_{y}\times{b_{y}}.\)

Скалярное произведения для векторов \(\overrightarrow{a}=(a_{x};a_{y};a_{z})\) и \(\overrightarrow{b}=(b_{x};b_{y};b_{z})\), которые расположены в трехмерном пространстве можно найти таким образом:

В рамках n-мерного пространства скалярное произведение векторов \(\overrightarrow{a}={a_{1}, a_{2},...,a_{n}}\) и \( \overrightarrow{b}={b_{1}, b_{2},...,b_{n}}\) возможно вычислить так:

\(\overrightarrow{a}\times{\overrightarrow{b}}=\overrightarrow{a_{1}}\times\overrightarrow{b_{1}}+\overrightarrow{a_{2}}\times{b_{2}}+...+a_{n\times{b_{n}}}\)

Примеры вычисления угла между двумя векторами

Задача 1

Начальные точки векторов находятся в начале координат. Нужно посчитать величину угла между векторами \(\overrightarrow{x}=(7,2)\) и \(\overrightarrow{y}=(4,5)\).

Угол между двумя векторами: \(\cos\phi=\frac{(x_{1}y)}{\mid{x}\mid\mid{y}\mid}=\frac{x_{1}y_{1}+x_{2}y_{2}}{\sqrt{x_{1}^{2}+x_{2}^{2}}\sqrt{{y_{1}^{2}+y_{2}^{2}}}}\).

Для того чтобы найти угол между векторами x и y нужно рассчитать нормы векторов x и y. Норма вектора \(\overrightarrow{x}\):\( \mid{x}\mid=\sqrt{x^{2}_{1}+x^{2}_{2}}=\sqrt{7\times7+2\times2}=\sqrt{53}\approx7.28\)

Норма вектора \(\overrightarrow{y}: \mid{y}\mid=\sqrt{y^{2}_{1}+y^{2}_{2}}=\sqrt{4\times4+5\times5}=\sqrt{41}\approx6.4\). Косинус угла между векторами \(\overrightarrow{x}\) и \(\overrightarrow{y}\) вычисляется следующим образом: \(\cos\phi=\frac{(x,y)}{\mid{x}\mid\mid{y}\mid}=\frac{x_{1}\times{y_{1}}+x_{2}\times{y_{2}}}{\mid{x}\mid\mid{y}\mid}=\frac{7\times4+2\times5}{7.28\times6.4}=0.816\).

Далее из данного уравнения можно рассчитать угол между векторами: \(\phi=35.3^{\circ}\).

Задача 2

Нужно найти угол между векторами \(\overrightarrow{a}=(1;-1)\) и \(\overrightarrow{b}=(1;2)\).

Решение:

\(\cos(\overbrace{\overrightarrow{a}\overrightarrow{b}})=\frac{\overrightarrow{a}\times\overrightarrow{b}}{\mid\overrightarrow{a}\mid\mid\overrightarrow{b}\mid}=\frac{1\times1+(-1)\times2}{\sqrt{1^{2}+(-1)^{2}}\times\sqrt{1^{2}+2^{2}}}=\frac{1-2}{\sqrt{2}\times\sqrt{5}}=\frac{-1}{\sqrt{10}}\)

\(\overbrace{\overrightarrow{a}\overrightarrow{b}}=\arccos(\frac{-1}{\sqrt{10}}=\arccos(\frac{-\sqrt{10}}{10}\)

Ответ: \(\overbrace{\overrightarrow{a}\overrightarrow{b}}=\arccos(\frac{-\sqrt{10}}{10}\)

Задача 3

Начальные точки векторов не совпадают. Нужно найти угол между векторами \(\overrightarrow{x}=AB\) и \(\overrightarrow{y}=CD, где A(-1;1), B (3;7), C (3;2), D (12;5)\).

Угол между двумя векторами: \(\cos\phi=\frac{(x_{1}y)}{\mid{x}\mid\mid{y}\mid}=\frac{(x_{1}\prime{y}\prime)}{\mid{x}\prime\mid\mid{y\prime\mid}}\frac{x\prime_{1}y\prime_{1}+x\prime_{2}y\prime_{2}}{\sqrt{(x_{1}\prime)^{2}+(x_{2}\prime)^{2}}\sqrt{{(y_{1}\prime)^{2}+(y_{2}\prime)^{2}}}} \).

Нужно переместить параллельно векторы \(\overrightarrow{x}\) и \(\overrightarrow{y}\) таким образом, чтобы начальные точки векторов начали совпадать с точкой начала координат. Получается следующее: \(\overrightarrow{x}\prime=(3-(-1);7-1)\), \(\overrightarrow{y}\prime=(12-3;5-2)=(9;3)\).

Угол \(\phi\) между \(\overrightarrow{x}\) и \(\overrightarrow{y}\) будет равен углу \(\phi\prime\) между векторами \(\overrightarrow{x}\prime\) и \(\overrightarrow{y}\prime\). Из-за этого при нахождении угла \(\phi\prime\) нам будет известна величина угла между векторами \(\overrightarrow{x}\) и \(\overrightarrow{y}.\)

Рассчитывается норма вектором \(\overrightarrow{x}\prime \overrightarrow{y}\prime\). Норма \(\mid\overrightarrow{x}\prime\mid=\sqrt{x^{2}_{1}+x^{2}_{2}}=\sqrt{4\times4+6\times6}=\sqrt52\approx7.21\)

Норма \(\mid\overrightarrow{y}\prime\mid=\sqrt{y^{2}_{1}+y^{2}_{2}}=\sqrt{9\times9+3\times3}=\sqrt90\approx9.49\).

Косинус угла между векторами \(\overrightarrow{x}\prime \overrightarrow{y}\prime: \cos\phi=\cos\phi\prime=\frac{x\prime,y\prime}{\mid{x}\prime\mid\mid{y}\prime\mid}=\frac{4\times9+6\times3}{7.21\times9.49}\approx0.79\). Угол между двумя векторами в итоге будет таков: \(\phi=\arccos(0.78)\approx37.81^{\circ}\).

Вывод

Вектор является прямой, которая имеет направление. Обозначение вектора: \(overrightarrow{b}\). Из статьи узнали как находить угол между векторами, как находить его при помощи скалярного произведения, векторного произведения и другими способами.

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Заметили ошибку?

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»