Этапы решения тригонометрических неравенств

Что такое тригонометрическое неравенство

Возникновение и становление тригонометрии как науки связано с развитием таких областей научных знаний, как астрономия, землемерия и строительное дело. В древние времена тригонометрические учения имели сугубо геометрический характер и использовались в «исчислении хорд».

С течением времени наука приобретала аналитический уклон. В начале XVIII века в тригонометрии произошло множество открытий и изменений, что обуславливает ее смещение в сторону математического анализа. Тогда же тригонометрические связи приобрели значения функций.

Современные школьники изучают тригонометрические законы и осваивают методы работы с такими выражениями на уроках математики. Необходимость в вычислении неизвестных в тригонометрических соотношениях разного характера возникает в процессе решения заданий по планиметрии, стереометрии, астрономии, физике и другим предметным областям.

Ежегодное итоговое тестирование учащихся также предусматривает наличие примеров из тригонометрии. Они отличаются от алгебраических наличием бесконечного числа корней. Это обстоятельство значительно усложняет задачу по их поиску. Кроме того, ответ на подобные примеры можно записать разными способами. Рассмотрим основные понятия по теме.

Если соотношения разделены одним из первых двух знаков, то такое неравенство называют строгим. При наличии знаков \(\leq\), \(\geq\) неравенства являются нестрогими.

Какие бывают

В зависимости от формы записи тригонометрические неравенства бывают двух видов:

• простейшие;
• сложные.

В первом случае для соотношения характерна простая запись, к примеру, \(\sin<\frac{1}{2}\). Решение подобных неравенств заключается в применении графиков.

В том случае, когда аргумент функции имеет в своей записи не только переменную, а целое выражение с неизвестной, неравенство называют сложным. Принцип и порядок действий при решении сложных неравенств несколько отличается от методики поиска корней для простого неравенства.

Решение тригонометрических неравенств, формулы

Существует несколько стандартных методик решения тригонометрических неравенств:

• графический метод;
• метод интервалов;
• с помощью единичной окружности.

Самыми простыми тригонометрическими неравенствами являются следующие соотношения:

• \(sinx\vee a\);
• \(cosx\vee a\);
• \(tgx\vee a\);
• \(ctgx\vee a\).

где \(\vee\) — один из знаков \(<,\;>,\;\leq,\;\geq, a\in R\).

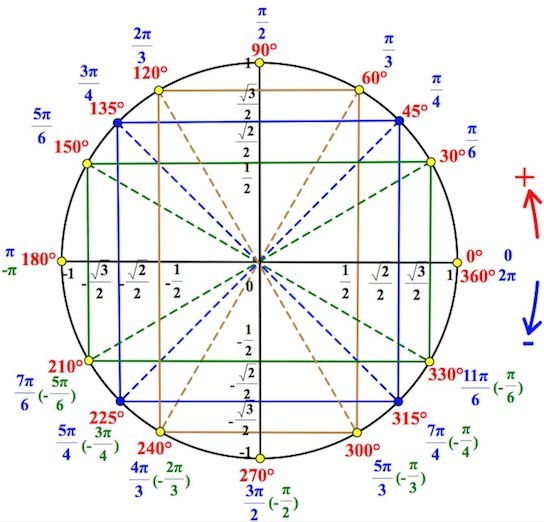
С целью разобраться с особенностями решений задач в тригонометрии необходимо освоить тригонометрический круг. С помощью окружности, на которой отмечены значения в градусах и радианах, можно находить корни для примитивных тригонометрических соотношений.

Источник: egemaximum.ru

Рассмотрим особенности применения разных методов решения тригонометрических неравенств на конкретных примерах.

Решение

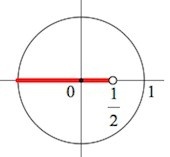
В данном случае целесообразно воспользоваться тригонометрическим кругом. Для этого обозначим на соответствующей оси косинусов точку \(\frac{1}{2}\). Заметим, что каждое из значений, которое меньше по сравнению с \(\frac{1}{2}\), расположено с левой стороны по отношению к \(\frac{1}{2}\) в пределах оси косинусов.

Источник: egemaximum.ru

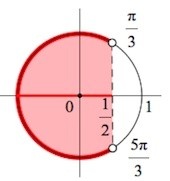
Далее необходимо обозначить множество точек в виде дуги, а именно, комплекс дуг, на тригонометрической окружности с косинусом, значение которого меньше по сравнению с \(\frac{1}{2}\).

Источник: egemaximum.ru

Дугу, которая получилась в итоге, следует пройти против направления часовой стрелки. Таким образом, от точки \(\frac{\pi}{3}\)  до последней точки \(\frac{5\pi}{3}\). Если указать не \(\frac{5\pi}{3}\), а точку \(-\frac{\pi}{3}\) , ответ получится неверный. Подобную ошибку совершают многие в процессе решений тригонометрических неравенств, поэтому следует быть внимательнее, проходя этот этап.

Заметим, что для данного в условии задачи неравенства характерны такие значения переменной:

\(\frac{\pi}{3}+2\pi n<x<\frac{5\pi}{3}+2\pi n,\;n\in Z.\)

Еще одним важным моментом является проверка правильного соотношения выбранных точек. Та, что находится правее, то есть вторая точка, должна быть больше по сравнению с той точкой, которая находится левее и является первой. Кроме того, нельзя пропустить следующую запись при формулировке ответа:

\(2\pi n,\;n\in Z.\)

Попробуем применить графический метод к поиску значений переменной для этого неравенства. В таком случае решение заключается в изображении координатной системы, а непосредственно само решение примет следующий вид:

Источник: egemaximum.ru

Ответ: \(\frac{\pi}{3}+2\pi n<x<\frac{5\pi}{3}+2\pi n,\;n\in Z.\)

Решение

Вновь обратимся к уже знакомому методу тригонометрического круга. Обозначим на оси косинусов записанное в условии задачи выражение:

\(-\frac{\sqrt2}{2}\).

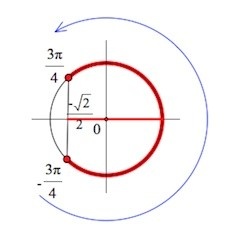
Если какое-либо значение, характерное для cos x превышает, либо соответствует \(-\frac{\sqrt2}{2}\), то оно расположено с правой стороны по отношению к точке \(-\frac{\sqrt2}{2}\). На рисунке обозначим красным цветом дугу с аргументами х, которые подходят под следующее условие:

\(cosx\geq -\frac{\sqrt2}{2}\)

Источник: egemaximum.ru

В результате получим:

\(-\frac{3\pi}{4}+2\pi n\leq x\leq \frac{3\pi}{4}+2\pi n,\; n\in Z\)

Ответ: \(-\frac{3\pi}{4}+2\pi n\leq x\leq \frac{3\pi}{4}+2\pi n,\; n\in Z\) 

Решение

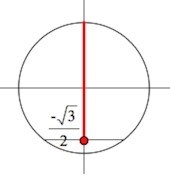
Рассмотрим ось косинусов на тригонометрической окружности. Отметим на ней \(-\frac{\sqrt3}{2}\). Если какое-либо из значений sin x превышает или является аналогичным \(-\frac{\sqrt3}{2}\), то оно расположено выше, чем точка \(-\frac{\sqrt3}{2}\).

Источник: egemaximum.ru

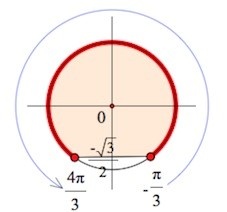
Далее перенесем выявленные ранее точки на тригонометрическую окружность.

Источник: egemaximum.ru

В результате получим следующие значения для переменной:

\(-\frac{\pi}{3}+2\pi n \leq x\leq \frac{4\pi}{3}+2\pi n,\;n\in Z\)

Ответ: \(-\frac{\pi}{3}+2\pi n \leq x\leq \frac{4\pi}{3}+2\pi n,\;n\in Z\)

 

Решение

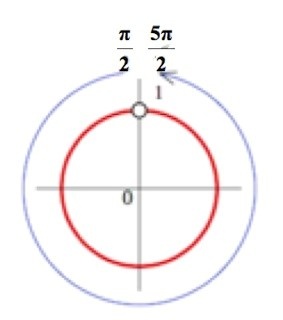
По аналогии с предыдущими примерами применим метод решения тригонометрических неравенств с помощью окружности к этой задаче.

Источник: egemaximum.ru

\(\frac{\pi}{2}+2\pi n<x<\frac{5\pi}{2}+2\pi n,\;n\in Z\)

Можно представить результирующий итог и в другой форме записи, к примеру:

все x, за исключением \(\frac{\pi}{2}+2\pi n,\;n\in Z\)

Ответ: \(\frac{\pi}{2}+2\pi n<x<\frac{5\pi}{2}+2\pi n,\;n\in Z.\)

 

Решение

Заметим, что исходное соотношение обладает таким же смыслом, что и следующее уравнение:

\(sin x = 1\)

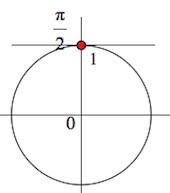
Это объясняется областью значений для функции \(y=sinx – [-1;1]\).

Источник: egemaximum.ru

В результате, получим ответ:

\(x=\frac{\pi}{2}+2\pi n,\;n\in Z.\)

Решение

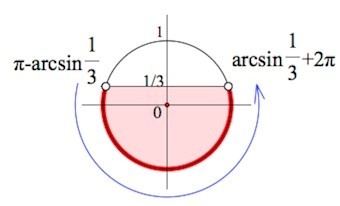
Задание нетривиальное и требует несколько иного подхода к решению. В первую очередь следует проделать все стандартные действия. Однако значение синуса нельзя найти по таблице. По этой причине обратимся к определению обратной тригонометрической функции, то есть арксинусу.

Источник: egemaximum.ru

Таким образом:

\(\pi -arcsin\frac{1}{3}+2\pi n<x<arcsin\frac{1}{3}+2\pi+2\pi n,\;n\in Z\)

Ответ: \(\pi -arcsin\frac{1}{3}+2\pi n<x<arcsin\frac{1}{3}+2\pi+2\pi n,\;n\in Z.\) 

На примере решения сложного тригонометрического неравенства разберем два метода: графический и с помощью интервалов. Это комбинация способов позволит справиться с самыми трудоемкими расчетами.

Решение

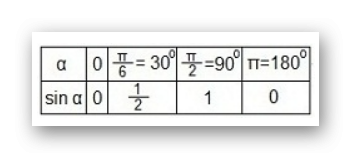
Если решать соотношение с помощью графика, то необходимо изобразить на координатной плоскости стандартную синусоиду y = sin x. При этом значения переменной допустимо выбрать любые. Для того чтобы определить опорные точки графика, следует составить таблицу:

Источник: karate-ege.ru

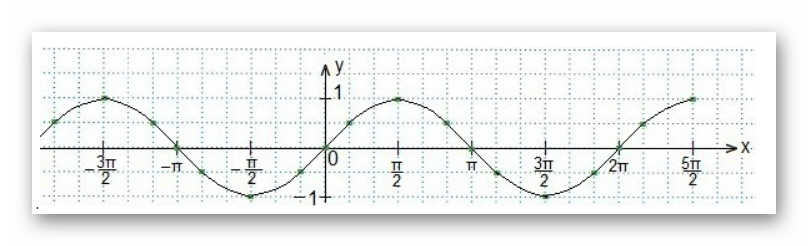
Заметим, что на графике  получилась кривая. Упростим решение примера путем замены сложного аргумента функции на новую переменную t:

\(\sin t < \frac{\sqrt{2}}{2}\)

Источник: karate-ege.ru

Далее необходимо построить прямую:

\(у = \frac{\sqrt{2}}{2}\)

Вычислим правую часть соотношения с помощью калькулятора, получим:

\(frac{\sqrt{2}}{2} \approx 0,71\)

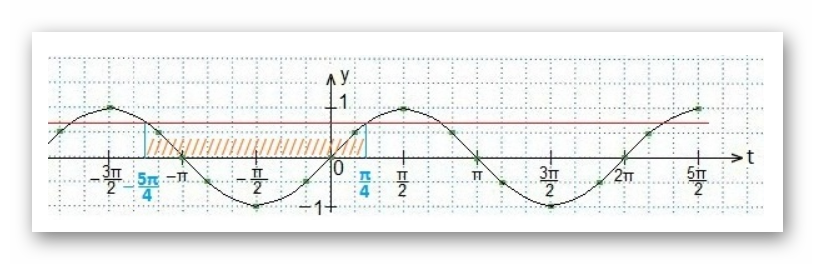
Графики пересекаются, что упрощает определение области искомых значений, в рамках которых обретает смысл условие задачи.

Источник: karate-ege.ru

Отрезок, который был определен, играет роль решения для введенной недавно переменной t:

\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)\(-\frac{5 \pi}{4}+2 \pi n < t < \frac{\pi}{4} + 2 \pi n, n\in Z\)

С другой стороны, для решения задачи требуется определить все вероятные значения для переменной х:

\(-\frac{5 \pi}{4}+2 \pi n < \frac{х}{2} + \frac{\pi}{3} < \frac{\pi}{4} + 2 \pi n\)

\(-\frac{5 \pi}{4}+2 \pi n < \frac{х}{2} + \frac{\pi}{3} < \frac{\pi}{4} + 2 \pi n\)

Решение двойного соотношения заключается в переносе \(\frac{\pi}{3}\) в крайние части неравенства и последующем проведении необходимых вычислений:

\(-\frac{5 \pi}{4} - \frac{\pi}{3} +2 \pi n < \frac{х}{2} < \frac{\pi}{4} - \frac{\pi}{3} + 2 \pi n\)

\(-\frac{19 \pi}{12} +2 \pi n < \frac{х}{2} < -\frac{\pi}{12} + 2 \pi n\)

\(-\frac{19 \pi}{6} +4 \pi n < х < -\frac{\pi}{6} + 4 \pi n\)

Ответ к задаче целесообразно записать как интервал для строго неравенства:

\((-\frac{19 \pi}{6} +4 \pi n; -\frac{\pi}{6} + 4 \pi n), n\in Z\)

\((-\frac{19 \pi}{6} +4 \pi n; -\frac{\pi}{6} + 4 \pi n), n\in Z\)

Ответ: \((-\frac{19 \pi}{6} +4 \pi n; -\frac{\pi}{6} + 4 \pi n), n\in Z\)

Нестандартные методы решения

Основные алгоритмы решения простых и сложных тригонометрических неравенств были рассмотрены ранее. Однако нередко в примерах встречаются соотношения такого типа, как «со звездочкой». Если попался такой пример, стоит выбрать один из следующих приемов поиска решений:

1. Используя принцип равносильных преобразований, следует записать сложное неравенство в виде простейших. При этом допустимо использовать те же методы, что и в процессе вычисления корней тригонометрического уравнения.
2. С помощью метода интервалов определить числовые промежутки, которым соответствуют решения заданного неравенства. Для этого необходимо решить соответствующее тригонометрическое уравнение и установить интервалы с расстановкой знаков плюс и минус, учитывая область определения неравенства.