Теорема синусов и косинусов для треугольника
Формулировка теоремы косинусов
Данная теорема связывает длины сторон треугольника с косинусом одного из его углов. Используя тригонометрию, получаем значения расстояний и углов, которые невозможно измерить другим способом. Теорема применяется, чтобы вычислить третью сторону фигуры по двум сторонам и вписанному в них углу, а также для вычисления углов, если известны все три стороны.
\(c^2 = a^2 + b^2 - 2ab cos(C)\)
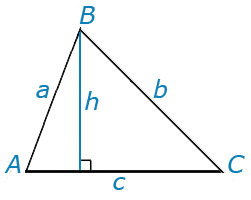
c — длина стороны, противоположной углу C, а a и b — другие стороны. Угол C — это угол между a и b.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: webmath.ru
Считается, что самое раннее известное изложение закона косинусов было сделано греческим математиком Евклидом в его книге «Элементы», написанной примерно в 300 году до нашей эры. Он был развит другими греческими математиками, в том числе Птолемеем, который широко использовал его в своих работах по астрономии и географии.
Формулы
Если вам известна длина всех трех сторон треугольника, вы можете использовать следующую формулу для нахождения косинуса одного из углов:
\(cos(C) = (a^2 + b^2 - c^2) / (2ab)\)
Если вам известна длина двух сторон и мера включенного угла треугольника, вы можете использовать следующую формулу для нахождения длины третьей стороны:
\(c^2 = a^2 + b^2 - 2ab cos(C)\)
Если известны длина двух сторон и длина угла, противолежащего неизвестной стороне, то для нахождения длины третьей стороны можно применить формулы:
\(c^2 = a^2 + b^2 - 2ab cos(C)\);
\(a^2 = b^2 + c^2 - 2bc cos(A)\);
\(b^2 = a^2 + c^2 - 2ac cos(B)\).
Во всех случаях a, b и c представляют собой длины, а A, B и C — меры углов, противоположных этим сторонам, соответственно.
Доказательство теоремы косинусов
Теорему можно доказать с помощью теоремы Пифагора и некоторых тождеств из тригонометрии.
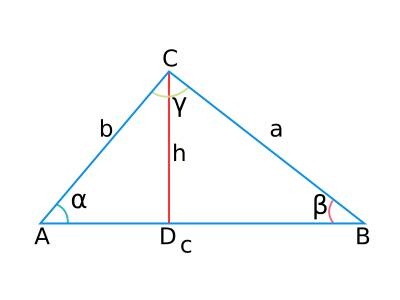
Рассмотрим треугольник ABC со сторонами длиной a, b и c, и углами напротив этих сторон с мерами A, B и C соответственно. Мы можем провести высоту из вершины B к противоположной стороне, разделив треугольник на два правильных треугольника. Пусть длина высоты равна h, а длина отрезка AM равна r.
В ΔABM мы имеем,
sin A = BM/AB = h/c
и, cos A = AM/AB = r/c
Из уравнений (1) и (2) получаем h = c(sin A) и r = c(cos A).
По теореме Пифагора в ΔBMC,
a2 = h2 + (b - r)2
Подставьте h = c(sin A) и r = c(cos A) в уравнение (3).
a2 = (c(sinA))2 + (b - c(cosA))2
= c2sin2A + b2 + c2cos2A - 2bc-cosA
= c2(sin2A + cos2A) + b2 - 2bc-cosA
= c2 + b2 - 2bc-cosA
Следовательно, доказано.
Задачи
Мальчик стоит в точке A, а две лодки расположены в точках B и C так, что положения всех трех образуют треугольник. Если угол A равен 36º, а длины AB и AC равны 70 см и 55 см соответственно, определите расстояние между двумя лодками, плавающими в озере.
Решение: Теорема косинуса выражается тремя различными способами. Мы будем использовать формулу a2 = b2 + c2 - 2bc-cos A, так как искомая сторона противоположна ∠A.
Подставьте 55 см для b, 70 см для c и 36º для угла A.
a2 = b2 + c2 - 2bc-cosA
a2 = (55)2 + (70)2 - 2(55)(70)cos 36º
a2 = 3025 + 4900 - (7700)(0.8)
a2 = 3025 + 4900 - 6160
a2 = 1765
a ≈ 42
Ответ: Длина поперек лодок равна 42 см.
У фермера есть огромное поле в форме треугольника. Две стороны поля имеют размеры 624 м и 327 м, а угол между ними равен 93º. Рассчитайте, сколько изгородей потребуется для ограждения поля?
Решение: Воспользуемся определением закона косинуса: a2 = b2 + c2 - 2bc-cosA.
Подставьте 624 вместо b, 327 вместо c и 93º вместо A.
a2 = b2 + c2 - 2bc-cosA
a2 = (624)2 + (327)2 - 2(624)(327)cos 93º
a2 = 389376 + 106929 - (408096)(-0.05)
a2 = 389376 + 106929 + 20404.8
a2 = 516709.8
a ≈ 719
Таким образом, периметр треугольного поля составляет 624 + 327 + 719 = 1670 метров.
Ответ: Фермеру потребуется 1670 метров изгороди.
Смежные стороны параллелограмма имеют размеры 6 см и 10 см, а угол между ними равен 79º. Можете ли вы определить длину диагонали параллелограмма?
Решение:
Дано: Пусть ABCD — параллелограмм, такой, что CD = 6 см, BC = 10 см.
Мы знаем, что смежные углы параллелограмма являются дополнительными.
Значит, ∠B = 180º - ∠C = 180º - 79º = 101º.
Также противоположные стороны параллелограмма равны.
Значит, AB = CD = 6 см.
Применим правило косинуса в ΔABC.
Подставьте 10 вместо a, 6 вместо c и 101º вместо B.
b2 = a2 + c2 - 2ac-cosB
b2 = (10)2 + (6)2 - 2(10)(6)cos101º
b2 = 100 + 36 - (120)(-0.19)
b2 = 100 + 36 + 22.8
b2 = 158.8
b ≈ 12.6
Ответ: Длина диагонали равна примерно 12,6 см.
Найдите длину третьей стороны треугольника, учитывая длины двух других сторон и меру включенного угла.
Дано: a = 8, b = 10, C = 45°
Решение: Используя вторую формулировку теоремы косинусов:
\(c^2 = a^2 + b^2 - 2ab cos(C)\)
\(c^2 = 8^2 + 10^2 - 2(8)(10) cos(45°)\)
\(c^2 = 64 + 100 - 160(0.7071)\)
\(c^2 = 164 - 113.14\)
\(c^2 = 50.86\)c
c ≈ 7.13
Следовательно, длина третьей стороны равна примерно 7,13 единиц.
Теорема синусов для треугольника
Источник: itest.kz
Теорема синусов связывает стороны и углы треугольника. Она гласит, что для любого треугольника отношение длины стороны к синусу угла, противолежащего этой стороне, одинаково для всех трех сторон. Эта теорема может быть записана несколькими способами, но одна из наиболее распространенных формулировок такова:
a / sin(A) = b / sin(B) = c / sin(C)
где a, b и c — длины сторон треугольника, а A, B и C — меры углов, противолежащих этим сторонам, соответственно. Эта формула может быть использована для решения любой из сторон или углов треугольника, если достаточно информации о других сторонах и углах.
Точное происхождение теоремы неизвестно. В Древней Индии тригонометрические функции широко использовались в астрономии и астрологии. Индийский астроном Арьябхата, живший в V веке нашей эры, использовал таблицы синусов для вычисления положения небесных тел.
Формулы
Она может быть сформулирована несколькими способами в зависимости от того, что известно о треугольнике.
Вот три возможных формулировки теоремы синусов:
Если известны длины двух сторон и мера угла, противолежащего одной из этих сторон, вы можете использовать следующую формулу для нахождения длины третьей стороны:
sin(C) = (c / a) sin(A) = (c / b) sin(B)
Если известны длины всех трех сторон треугольника, вы можете воспользоваться следующей формулой для нахождения меры одного из углов:
sin(A) / a = sin(B) / b = sin(C) / c
Если известна длина одной стороны и меры углов, противолежащих этой стороне и другому углу, то для нахождения длины другой стороны применяется формула:
b / sin(B) = c / sin(C) = 2R
где R — радиус окружности треугольника.
В каждой из этих формул a, b и c представляют собой длины сторон треугольника, а A, B и C — меры углов, противоположных этим сторонам, соответственно.
Задачи
Найдите длину стороны треугольника, учитывая длины двух сторон и меру угла, противолежащего одной из этих сторон. Дано: a = 8, b = 10, A = 60°
Решение: Мы можем использовать первую формулировку теоремы синусов:
sin(C) = (c / a) sin(A) = (c / b) sin(B)
Найдем sin(C):
sin(C) = (c / a) sin(A)
sin(C) = (c / 8) sin(60°)
sin(C) = (c / 8) (sqrt(3) / 2)
sin(C) = (c sqrt(3)) / 16
Теперь мы можем использовать тот факт, что сумма углов в треугольнике равна 180 градусам, чтобы найти меру угла C:
C = 180° - A - B
C = 180° - 60° - sin-¹(sin(C) / sin(A))
C ≈ 53.13°
Наконец, мы можем использовать вторую формулировку теоремы синусов, чтобы найти длину стороны c:
sin(C) / c = sin(A) / a
c = sin(C) / sin(A) * a
c = (c sqrt(3)) / (16 sin(60°)) * 8
c ≈ 7.32
Следовательно, длина стороны c равна примерно 7,32 единицы.
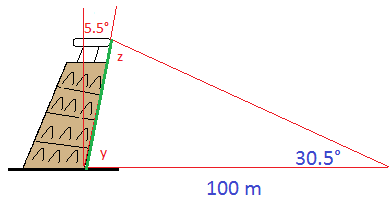
Пизанская башня наклонена на 5,5 градусов от вертикали. На расстоянии 100 метров от стены башни угол возвышения к вершине составляет 30,5 градуса. Используя закон синусов, оцените высоту наклонившейся башни (высота показана на рисунке ниже зеленой линией).
Решение:
Обратите внимание, что высота показана зеленой линией.
Источник: basic-mathematics.com
Найдем угол y и угол z. Угол y + 5,5 = 90, поэтому угол y = 84,5
Для нахождения неизвестной высоты Пизанской башни недостаточно знать значение угла y. Вы должны знать значение угла z.
84,5 + 30,5 + угол z =180
115 + угол z = 180
угол z = 65
Теперь мы можем использовать закон синусов.
sin(65°) / 100 = 0.00906
sin(30.5°) / высота башни
= 0.00906
Высота башни = sin(30.5°) / 0.00906
Высота башни = 56 метров.
В действительности высота Пизанской башни составляет 55,86 метров.
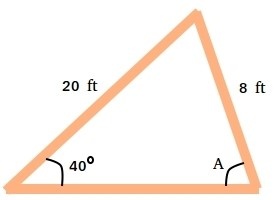
Владелец дома пытается построить приподнятую садовую грядку треугольной формы. Сосед дал ему два куска пиломатериалов длиной 20 футов и 8 футов, и он сложил их вместе, чтобы начать треугольник. Он планирует пойти в магазин, чтобы купить третий кусок пиломатериала для завершения треугольника. Он хочет построить треугольный сад так, чтобы третий кусок пиломатериала составлял угол 40 градусов с куском длиной 20 футов. Получится ли у него сделать сад? Если да, то какой длины должен быть третий кусок пиломатериала?
Источник: basic-mathematics.com
Если домовладелец сможет построить такой сад, то он будет выглядеть так. Между третьим куском пиломатериала и куском длиной 8 футов будет образован угол A.
Воспользуемся законом синусов, чтобы проверить, возможно ли это.
sin (40 градусов) / 8 = sin (A) / 20
0,642 / 8 = sin (A) / 20
0,08025 = sin (A) / 20
Умножьте обе стороны уравнения на 20
0,08025(20) = [sin (A) / 20](20)
0.08025(20) = sin (A)
0.08025(20) = sin (A)
1.605 = sin (A)
Синус угла должен быть меньше 1. Поскольку угол A не может быть образован, сделать такой сад не получится. Поскольку угол не может быть образован, отрезок длиной 8 футов никогда не встретится с третьим отрезком. В результате он никогда не узнает длину третьего отрезка.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так