Что нужно знать о теореме Пифагора — основные сведения
Теорема Пифагора — краткая история
Теорема Пифагора является одной из ключевых теорем евклидовой геометрии. С ее помощью было установлено простое отношение между сторонами в прямоугольном треугольнике. Таким образом, длины катетов, возведенные в квадрат, в сумме дают квадрат длины гипотенузы, что можно использовать при их нахождении.
Данное соотношение по предположению ученых являлось знанием различных цивилизаций древности, существовавших во времена до нашей эры. Считается, что первым доказал теорему с геометрической точки зрения Пифагор. Это интересное утверждение сформулировано в Предложении 47 в «Началах» Евклида.
Геометрическая интерпретация теоремы Пифагоры свидетельствует о том, что площадь квадрата изображенного на гипотенузе, вычисляется, как сумма площадей, которыми характеризуются квадраты, лежащие на катетах.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Справедливым является и обратное утверждение, согласно которому в прямоугольном треугольнике длины пары сторон, возведенные в квадрат, в сумме дают квадрат длины третьей стороны.
Предусмотрены объемные обобщения записанной теоремы с объяснениями в случаях с произвольными треугольниками и фигурами, рассматриваемых в пространствах высших размерностей. В неевклидовых геометриях теорема Пифагора не применима.
Происхождение концепции теоремы Пифагоры связывают с древним Египтом и Вавилоном (примерно 1900 г. до нашей эры). Изображение на вавилонской табличке возрастом около 4 тысяч лет, изготовленной из глины, отражает связь между катетами и гипотенузой в прямоугольном треугольнике. С другой стороны, это утверждение получило распространение в результате высказываний Пифагора (6 век до нашей эры).
Формулировка теоремы
Теорема Пифагора: в прямоугольном треугольнике гипотенуза в квадрате определяется, как квадраты катетов в сумме, то есть:
\(c^{2} = a^{2} + b^{2}.\)
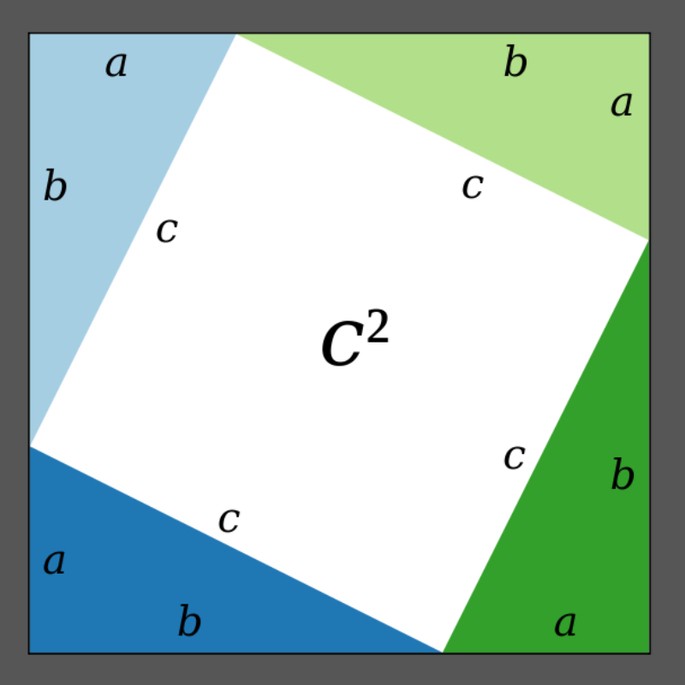
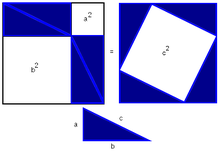
Данную теорему можно доказать с точки зрения алгебры. Изобразим условия на рисунке:
Стороны с образуют квадрат, как видно на чертеже. Результат получился путем построения четырех идентичных треугольников abc. Заметим, что любая из сторон квадрата в длину составляет:
\(a + b\)
Вычислим площадь квадрата:
\(A = (a + b) (a + b)\)
Площадь минимального квадрата, расположенного во внутренней области равна \(c^{2}\). Любой из изображенных треугольников имеет площадь \(\frac{ab}{2}\). Таким образом, суммарная площадь треугольников равна:
\(4\frac{ab}{2} = 2ab\)
Самый маленький из двух квадратов и треугольники по площади равны:
\(A = c^{2} + 2ab\)
Зная, что площадь большего квадрата складывается из площадей маленького квадрата и всех треугольников, запишем следующее соотношение:
\((a + b) (a + b) = c^{2} + 2ab\)
\(a^{2} + 2ab + b^{2} = c^{2} + 2ab\)
\(a^{2} + b^{2} = c^{2}\)
Утверждение доказано.
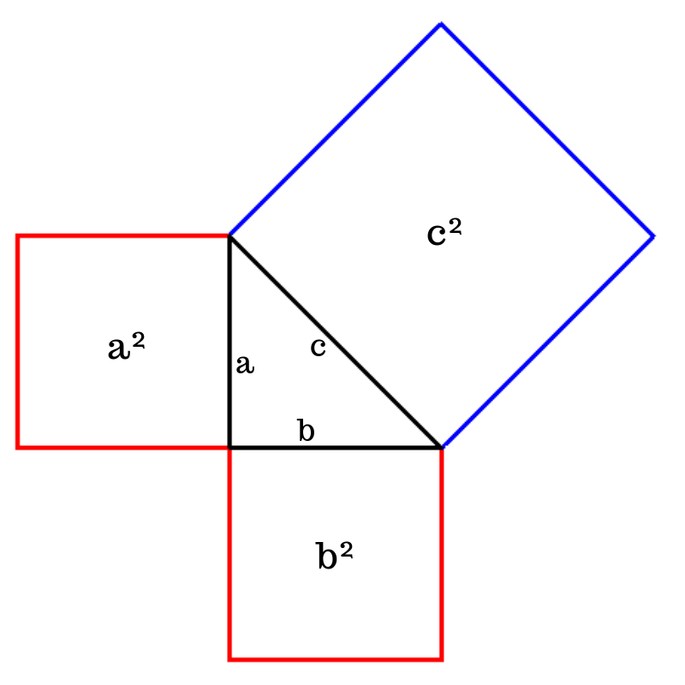
Существует еще одно доказательство теоремы Пифагора, которая будет звучать, как: «Пифагоровы штаны на все стороны равны».
На рисунке с играет роль гипотенузы, а катеты обозначены за a и b. Опустим перпендикуляр к гипотенузе и назовем его с.
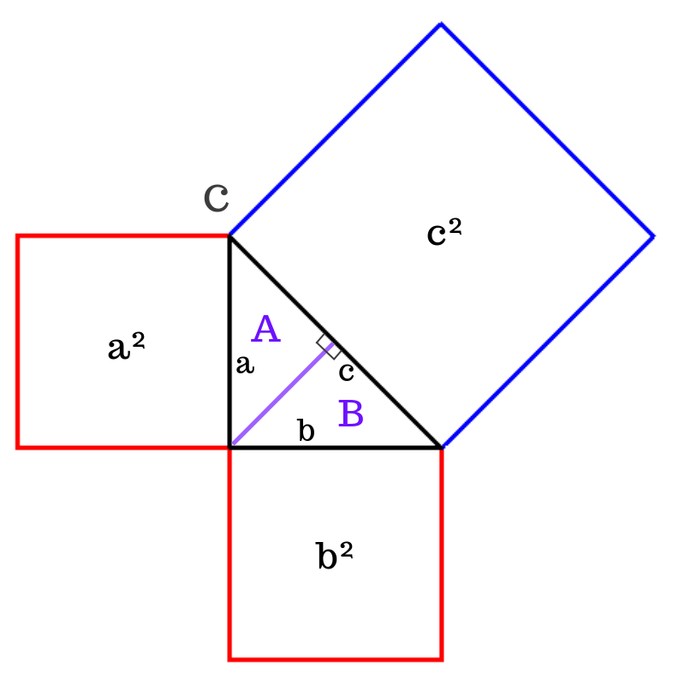
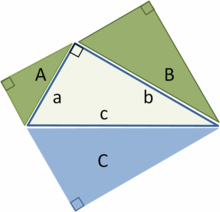
В результате получилось построить два треугольника (А и В), являющиеся прямоугольными, которые расположены во внутреннем пространстве крупного треугольника С. Тогда по факту его площадь складывается из площадей двух новых треугольников:
\(С = А + В\)
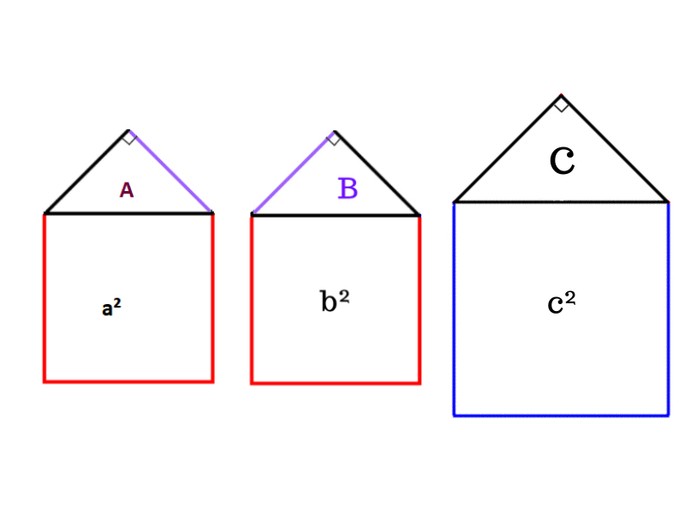
Далее попробуем разделить «Пифагоровы штаны» и создать 3 аналогичные фигуры.
Заметим подобие трех треугольников, что позволяет считать подобными полученные фигуры в виде домиков. Таким образом, соотношение площади A и \(a^{2}\) будет одинаковым с площадью \(B\) и \(b^{2}\), а также с площадью \(C\) и \(c^{2}\):
\(\frac{А}{ a^{2}} = \frac{В}{ b^{2}} =\frac{С}{с ^{2}} = \beta\)
Площадь любого из треугольников можно вычислить с помощью площади каждого из квадратов:
\(A = \beta \cdot a^{2}\)
\(B = \beta \cdot b^{2}\)
\(C = \beta \cdot с^{2}\)
Таким образом:
\(С = А + B\)
\(\beta \cdot с^{2} = \beta \cdot a^{2} + \beta \cdot b^{2}\)
\(a^{2} + b^{2} = c^{2}\)
Теорема доказана.
Доказательства теоремы
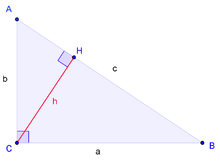
Рассмотрим способ доказательства теоремы Пифагоры с помощью треугольников, которые являются подобными. В процессе следует ориентироваться на следующий рисунок:
Треугольник \(\triangle ABC\) является прямоугольным, так как имеет прямой угол. Обозначим его вершину за С, а стороны назовем, как a,b,c. Эти стороны расположены противоположно вершинам треугольника A,B,C соответственно.
Проведем высоту CH. Руководствуясь признаком подобия треугольников, запишем:
\(\triangle ABC\sim \triangle ACH\)
\(\triangle ABC\sim \triangle CBH\)
В результате получим:
\({\frac {a}{c}}={\frac {|HB|}{a}},\quad {\frac {b}{c}}={\frac {|AH|}{b}}\)
Если найти произведение крайних элементов пропорций, то получится следующее соотношение:
\(a^{2}=c\cdot |HB|,\quad b^{2}=c\cdot |AH|\)
Далее целесообразно сложить компоненты:
\(a^{2}+b^{2}=c\cdot {\big (}|HB|+|AH|{\big )}=c^{2}\quad \Leftrightarrow \quad a^{2}+b^{2}=c^{2}\)
Таким образом, теорема доказана.
К доказательству теоремы Пифагора применим метод площадей. Данный способ характеризуется высокой степенью сложности. Разберем основные приемы доказательств.
Рассмотрим доказательство на основе равнодополняемости. Для этого следует воспользоваться следующей схемой:
В данном случае предлагается исследовать 4 аналога треугольника, который является прямоугольным, имеет катеты a,b и гипотенузу c. Стороны изображены так, что образуется квадрат, сторона которого равна a+b.
Во внутреннем пространстве можно распознать четырехугольник со стороной с. Это квадрат, так как в сумме пара противолежащих прямому углу острых углов дает 90 градусов, а мера развернутого угла составляет 180 градусов.
Площадь большого квадрата:
\( (a+b)^{2}\)
Площадь внутреннего квадрата \(c^{2}\), а площадь каждого из треугольников равна:
\(\frac {ab}{2}\)
Тогда:
\((a+b)^{2}=4\cdot {\frac {ab}{2}}+c^{2}\)
При алгебраическом преобразовании следует утверждение теоремы.
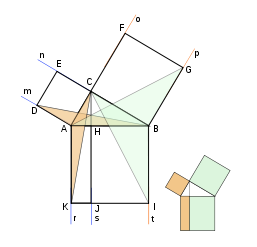
Доказательство Евклида построено на подтверждении конгруэнтности \(\triangle ACK\cong \triangle ABD\) с площадями, соответствующими половине площади прямоугольников \(AHJK\) и \(ACED\).
Традиционное доказательство Евклида позволяет установить, что площади между прямоугольниками равны. Данные прямоугольники получены в результате разделения квадрата над гипотенузой с помощью высоты, проведенной из прямого угла. Согласно описанной на рисунке схеме можно установить, что площадь квадрата над гипотенузой, который образован прямоугольниками \(AHJK\) и \(BHJI\), вычисляется, как сумма площадей квадратов над катетами.
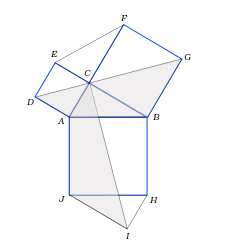
Доказательство Леонардо да Винчи изображено схематично на рисунке:
Доказательство Леонардо да Винчи построено на подтверждении конгруэнтности четырехугольников CAJI и DABG. Данные фигуры обладают площадями, которые можно определить путем сложения половин площадей квадратов на катетах и площади начального треугольника. Такой же результат получается, если к половине площади квадрата на гипотенузе прибавить значение площади, которой обладает начальный треугольник. В результате половина суммы площадей квадратов над катетами соответствует половине площади квадрата над гипотенузой, что является утверждением, равносильным геометрической формулировке теоремы Пифагора.
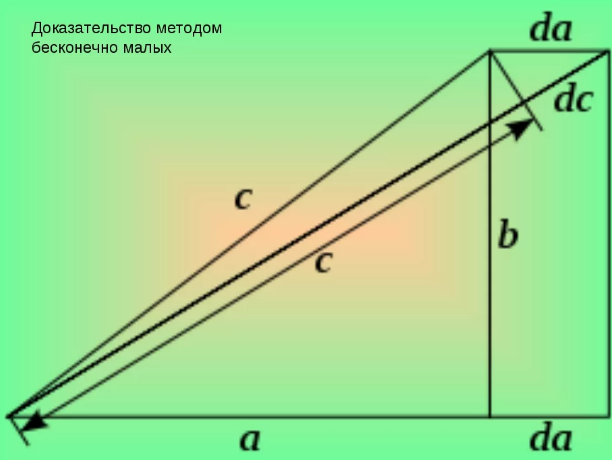
Схема доказательства методом бесконечных малых:
Известно несколько способов подтверждения теорем с помощью дифференциальных равенств. Например, считается, что Харди удалось доказать теорему Пифагора, применяя бесконечно малые приращения катетов а и b, а также гипотенузы c.
Приращение катета da, если неизменным остается катет b, сопровождается приращением гипотенузы dc, что можно записать следующим образом:
\(\frac {da}{dc} = \frac {c}{a}\)
Путем разделения неизвестных целесообразно сформулировать такое дифференциальное уравнение:
\(c\,dc = a\,da\)
В результате интегрирования записанного равенства получим:
\(c^{2}=a^{2}+\mathrm {const}\)
Исходные условия:
\(a=0,\ c=b\)
Таким образом, константа равна:
\(b^{2}\)
В итоге теорема доказана.
Вариации и обобщения
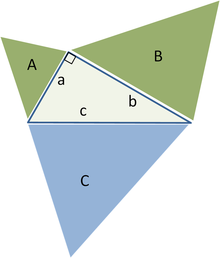
Рассмотрим обобщение теоремы Пифагора для геометрических фигур, которые являются подобными, на трех сторонах. К примеру, на рисунке площади закрашенных зеленым цветом фигур в сумме дают площадь фигуры, выделенной синим цветом:
Теорема Пифагора с использованием подобных прямоугольных треугольников:
Обобщение теоремы Пифагора с точки зрения геометрии представлено Евклидом в «Началах». Согласно утверждению, площади фигур, которые изображены на катетах, в сумме дают площадь подобной им фигуры, которая расположена на гипотенузе. Смысл обобщения состоит в пропорциональности площади подобной фигуры квадрату какого-либо собственного линейного размера и в частности квадрату длины какой-то из сторон. Таким образом:
\({\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}\,\Rightarrow \,A+B={\frac {a^{2}}{c^{2}}}C+{\frac {b^{2}}{c^{2}}}C\)
Заметим, что согласно теореме Пифагора, справедливо следующее соотношение:
\(a^{2}+b^{2}=c^{2}\)
В результате:
\(A+B=C\)
Следующим обобщением является теорема косинусов. Известно, что теорема Пифагора является ее частным случаем. С помощью данного обобщения установлена связь между длинами сторон в треугольнике, который является произвольным. Таким образом:
\(a^{2}+b^{2}-2ab\cos {\theta }=c^{2}\)
Здесь \(\theta\) обозначает угол, расположенный между сторонами а и b.
В том случае, когда градусная мера угла составляет 90°, \(\cos \theta\) принимает нулевое значение, что позволяет упростить соотношение до классической теоремы Пифагора.
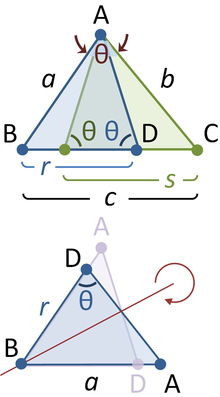
Обобщение, которое установил Сабит ибн Курра, продемонстрировано на рисунке:
В нижней части изображены подобные треугольники \(\triangle DBA\) и \(\triangle ABC\).
Известно о существовании обобщения теоремы Пифагора на произвольный треугольник, в основе которого лежит отношение длин сторон этой геометрической фигуры. Нужно выполнить построение равнобедренного треугольника в области начального произвольного треугольника таким образом, что их вершины совпадают, а основание равнобедренного треугольника лежит на стороне с. При этом углы при основании аналогичны углу \(\theta\), который расположен напротив стороны c. Сравнение двух треугольников, которые подобны первому, позволяет вывести следующее соотношение:
\(a^{2}+b^{2}=c(r+s)\)
Данное выражение можно преобразовать в теорему Пифагора при условии, что \(\theta =\pi /2\). Из подобия полученных фигур вытекает такое следствие:
\({\frac {c}{a}}={\frac {a}{r}},\quad {\frac {c}{b}}={\frac {b}{s}}\quad \Rightarrow \quad cr+cs=a^{2}+b^{2}\).
Практическое применение теоремы
Теорема Пифагора имеет прикладное значение. В первую очередь стоит отметить применение рассмотренной закономерности для измерения расстояния, на которое удалены две некоторые точки, находящиеся в прямоугольной системе координат:
\(s={\sqrt {(a-c)^{2}+(b-d)^{2}}}\)
Здесь s является расстоянием, а точки имеют следующие координаты (a, b) и (c,d).
Теорема Пифагора применима, когда требуется решить задачу на определение модуля комплексного числа. При условии, что \(z=x+yi\), модуль вычисляется, как длина радиус-вектора на комплексной плоскости к точке с координатами (x,y):
\(|z|={\sqrt {x^{2}+y^{2}}}\)
С помощью теоремы Пифагора удобно находить расстояние, на которое удалены некие комплексные числа \(z_{1}=x_{1}+y_{1}i\) и \(z_{2}=x_{2}+y_{2}i\). В этом случае целесообразно применить следующую формулу:
\(|z_{1}-z_{2}|={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}\)
Применительно к паре точек, расположенных в плоскости Лобачевского, теорема Пифагора позволит найти расстояние между ними таким образом:
\(ds^{2}=dx^{2}+\operatorname {ch} ^{2}\left({\frac {y}{R}}\right)dy^{2}\)
В этом случае R обозначает радиус кривизны плоскости Лобачевского, ch является обозначением гиперболического косинуса.
Применение теоремы Пифагора в Евклидовой метрикt позволяет определить удаленность точек \(p=(p_{1},\dots ,p_{n})\) и \(q=(q_{1},\dots ,q_{n})\) друг от друга в n-мерном пространстве с помощью формулы:
\(d(p,q)={\sqrt {\sum _{i=1}^{n}{(p_{i}-q_{i})^{2}}}}\),
где d(p,q) обозначает расстояние между рассматриваемыми точками.
Рассмотрим, как теорема Пифагора применяется в теории чисел. Пифагоровой тройкой называют совокупность их трех натуральных чисел (\(x,\;y,\;z\)). Данные числа допустимо принять за значения длин сторон, из которых состоит прямоугольный треугольник. Таким образом, это натуральные числа, соответствующие диофантову соотношению:
\(x^{2}+y^{2}=z^{2}\)
Пифагоровы тройки имеют огромное значение для понятной формулировки и проверки теории чисел. С помощью их результативного определения образован обширный объем работ, выполненных в разные времена, начиная с древности. Представление Великой теоремы Ферма является аналогичным задаче вычисления пифагоровых троек для степени более 2.
Лишь одна пифагорова тройка, в состав которой входят три последовательных числа подряд, имеет вид 3, 4, 5:
\(3^{2}+4^{2}=5^{2}.\)
Примеры решения задач
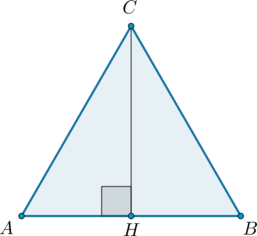
Треугольник АВС обладает следующими параметрами:
угол \(C = 90^\circ\)
угол \(A = 30^\circ\)
\(AB=2\sqrt3.\)
Требуется посчитать, чему равна высота \(СН\).
Решение
Заметим, что катет, который расположен напротив угла в \(30^\circ\), составляет половину от гипотенузы. В таком случае:
\(BC=0,5AB=\sqrt3\)
Запишем свойство прямоугольного треугольника:
\(\angle BCH=\angle A=30^\circ\)
В результате:
\(\triangle BCH: HB=0,5 BC=\sqrt3:2.\)
Воспользуемся теоремой Пифагора:
\(\triangle BCH: CH=\sqrt{BC^2-BH^2}=\sqrt{\dfrac94}=1,5\)
Ответ: 1,5.
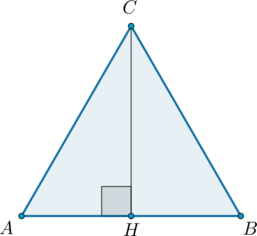
Треугольник АВС характеризуется следующими параметрами:
угол \(C = 90^\circ\)
\(CH\) обозначает высоту
угол \(A = 30^\circ\)
Необходимо определить АН при условии, что \(АВ = 2.\)
Решение
Заметим, что катет, который расположен напротив угла в \(30^\circ\), составляет половину от гипотенузы. В таком случае:
\(BC=0,5AB=1\)
Воспользуемся теоремой Пифагора:
\(\triangle ABC: AC=\sqrt{AB^2-BC^2}=\sqrt3\)
\(\triangle AHC: HC=0,5AC=\sqrt3:2\)
\(AH=\sqrt{AC^2-HC^2}=1,5\)
Ответ: 1,5.
Задан некий треугольник АВС, в котором градусная мера угла С составляет \(90^\circ\), СН обозначает высоту, градусная мера угла А составляет \(30^\circ\). Нужно вычислить ВН при условии, что АВ = 4.
Решение
Заметим, что катет, который расположен напротив угла в \(30^\circ\), составляет половину от гипотенузы. В таком случае:
\(BC=0,5AB=2\)
Воспользуемся свойством прямоугольного треугольника:
\(\angle BCH=\angle A=30^\circ\)
В результате:
\(\triangle BCH: HB=0,5 BC=1\)
Ответ: 1.
Имеется некий треугольник АВС, в котором \(AB=BC=AC=2\sqrt3\). Необходимо вычислить высоту СН.
Решение
Заметим, что:
\(AC=BC\)
В таком случае, СН представляет собой медиану. В результате:
\(AH=0,5 AB=\sqrt3.\)
Воспользуемся теоремой Пифагора:
\(\triangle ACH: CH=\sqrt{AC^2-AH^2}=3\)
Ответ: 3.
Треугольник АВС является равносторонним. Высота \(СН = 2\sqrt3\). Требуется определить АВ.
Решение
Заметим, что:
В таком случае, СН представляет собой медиану. В результате решение будет выглядеть следующим образом:
AH=a
\(AB=AC=2a\)
Воспользуемся теоремой Пифагора, которая гласит следующее:
\(\triangle ACH: AC^2=AH^2+CH^2\quad\Rightarrow\quad 4a^2=a^2+12\quad\Rightarrow\quad a=2\quad\Rightarrow\quad AB=2a=4\)
Ответ: 4.
Имеется некий треугольник АВС, в котором АС равна ВС. Высота АН соответствует 4, градусная мера угла С составляет \(30^\circ\). Нужно определить ВС.
Решение
В прямоугольном треугольнике \(\triangle ACH\) катет, который расположен напротив угла \(30^\circ\), соответствует половине гипотенузы. В результате верным является такой вариант:
\(4=AH=0,5AC\)
Таким образом, вывод:
\(8=AC=BC\)
Ответ: 8.
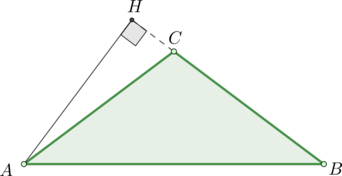
Треугольник АВС характеризуется следующими параметрами:
\(AC=BC=2\sqrt3\)
\(\angle C=120^\circ\)
Необходимо определить, чему равна высота АН.
Решение
В прямоугольном треугольнике \(\triangle ACH\):
\(\angle ACB=120^\circ\)
В результате:
\(\angle ACH=180^\circ-120^\circ=60^\circ\)
Таким образом:
\(\angle HAC=90^\circ-60^\circ=30^\circ\)
Катет, который расположен напротив угла \(30^\circ\), соответствует половине гипотенузы, поэтому:
\(HC=0,5AC=\sqrt3\)
Воспользуемся теоремой Пифагора:
\(AH=\sqrt{AC^2-HC^2}=3\)
Ответ: 3.
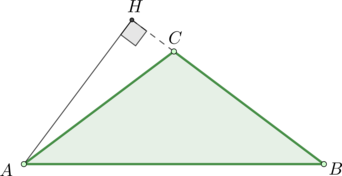
Треугольник АВС характеризуется следующими параметрами:
\(AC=BC\)
\(\angle C=120^\circ\)
\(AB=2\sqrt3\)
Необходимо узнать величину АС.
Решение
Проанализируем прямоугольный \(\triangle AHB\):
Заметим, что:
\(\angle C=120^\circ\)
AC=CB
В таком случае:
\(\angle B=(180^\circ-120^\circ):2=30^\circ\)
Катет, который расположен напротив угла \(30^\circ\), соответствует половине гипотенузы, поэтому:
\(HA=0,5AB=\sqrt3\)
В прямоугольном \(\triangle ACH\):
\(\angle ACB=120^\circ\)
\(\angle ACH=180^\circ-120^\circ=60^\circ\)
В результате:
\(\angle HAC=90^\circ-60^\circ=30^\circ\)
Таким образом:
\(HC=0,5AC\)
Воспользуемся теоремой Пифагора:
\(AC^2=HC^2+HA^2\quad\Rightarrow\quad AC^2=\dfrac{AC^2}4+3\quad\Rightarrow\quad AC=2\)
Ответ: 2.
Имеется некий треугольник \(АВС\), в котором \(AC=BC\), \(\angle C=120^\circ, AC=2\sqrt3\). Требуется вычислить \(АВ\).
Решение
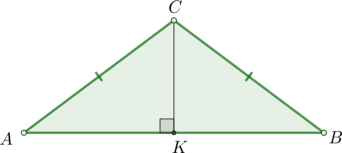
Построим \(СК\perp AB\):
В равнобедренном \(\triangle ABC\) отрезок СК играет роль медианы и биссектрисы. В результате:
\(AK=0,5AB\)
\(\angle ACK=60^\circ\)
В таком случае:
\(\angle CAK=90^\circ-60^\circ=30^\circ\)
Катет, который расположен напротив угла \(30^\circ\), соответствует половине гипотенузы, поэтому:
\(CK=0,5AC=\sqrt3\)
Воспользуемся теоремой Пифагора:
\(AK=\sqrt{AC^2-CK^2}=3\quad\Rightarrow\quad AB=2AK=6\)
Ответ: 6.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так