Теорема Менелая для треугольника

Формулировка теоремы Менелая

Теорема Менелая гласит: если взять любую прямую, которая трансверсирует (пересекает) три стороны треугольника (одну из них придется продлить), то на сторонах отсекаются шесть отрезков. Произведение трех не смежных отрезков равно произведению трех других. Обратное также справедливо. Обычно эти два произведения выражаются соотношением, равным 1 или -1, если используются направленные отрезки.

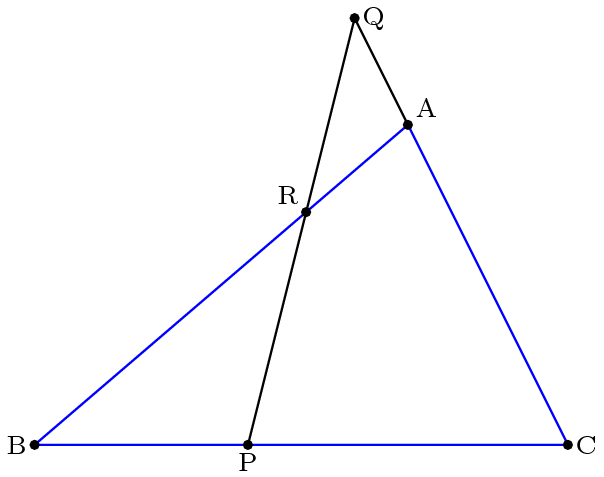
Если прямая PQ, пересекающая AB на ▲ABC, где P лежит на BC, Q является продолжением AC, R на пересечении PQ и AB, тогда:

(PB/CP) * (QC/QA) * (RA/RB) = 1.

Источник: artofproblemsolving.com

В другом случае, если записать теорему с помощью направленных отрезков, она приобретает вид BP * CQ * AR = CP * QA * RB. Кроме того, теорема работает для всех трех точек, лежащих на продолжении соответствующих сторон.

Доказательство

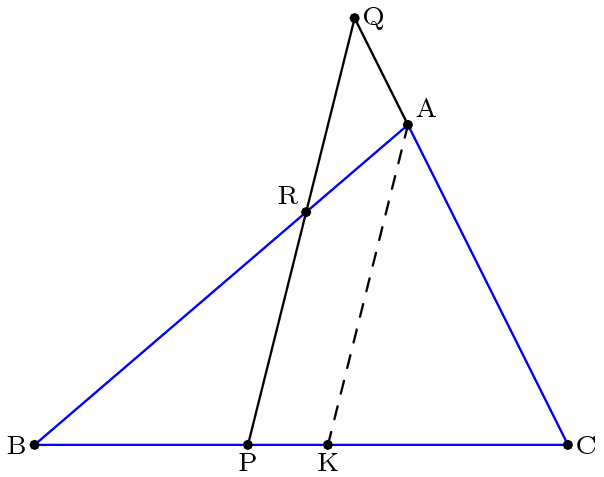
1. Доказательство с помощью подобных треугольников.

Источник: artofproblemsolving.com

Провести прямую, параллельную QP, через A и пересекающую BC в точке K:

▲RBP ≈ ▲ABK → (AR/RB)=(KP/PB)

▲QCP ≈ ▲ACK → (QC/QA)=(CP/KP)

Умножив два равенства вместе, чтобы исключить фактор PK, получим:

(AR/RB) * (QC/QA) = CP/PB → (AR/RB) * (QC/QA) * (PB/CP) = 1.

2. Доказательство с помощью барицентрических координат.

Предположим, что мы зададим точкам P, Q, R следующие координаты:

P: (0, P, 1-P)

R: (R , 1-R, 0)

Q: (1-Q ,0, Q)

Обратите внимание, что здесь сказано следующее:

CP/PB = (1-P)/P

BR/AR = (1-R)/R

QA/QC = (1-Q)/Q

Линия, проходящая через R и P, задается: |X 0 R | = 0. |Y P 1-R| = 0. |Z 1-P 0| = 0.

что после упрощения дает:

-X*(R-1)(P-1)+Y*R(1-P)-Z*PR = 0
Z*PR = -X*(R-1)(P-1)+Y*R(1-P).

Подставляя координаты для Q, получаем (Q-1)(R-1)(P-1) = QPR. Из (CP/PB)=(1-P)/P, мы имеем:

P=(1-P)*PB / CP.

Аналогично: R=(1-R)*AR / BR.

Q=(1-Q)*QC / QA.

Подставляя эти значения, получаем (Q-1)(R-1)(P-1) = ((1-Q) * QC * (1-P) * PB * (1-R) * AR) / QA * CP * BR)) что упрощается до QA * CP * BR = -QC * AR * PB.

3. Доказательство с помощью точек массы.
Сначала определим некоторые массы.

B_m1, C_m2 и Q_m3.

С помощью точек масс:

BP*m1=PC*m2 → BP/CP=m2/m1.

QC/QA = (AC+QA)/QA = 1+(AC/QA) = 1+(m3/m2) = (m2/m2)+ (m3/m2) = (m3+m2) / m2.

The масса в точке A равна m3+m2

AR*(m3+m2) = RB*m1 → AR/RB = m1 / (m3+m2).

Умножая их вместе, получаем: BP/CP * QC/QA * AR/RB = m2/m1 * (m3+m2)/m2 * m1/(m3+m2) = 1.

Обратная теорема Менелая

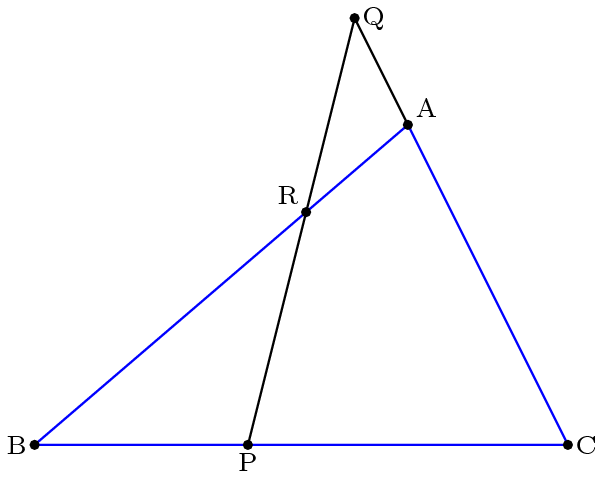
Обратная теорема Менелая также верна. Если (BP/PC) * (CQ/QA) * (AR/RB) = 1 на приведенной ниже диаграмме, то P, Q, R коллинеарны. Обратное утверждение полезно при доказательстве того, что три точки коллинеарны.

Источник: artofproblemsolving.com

Применение

Используя известные длины отрезков, находят отношение, в котором биссектрисы делят противоположные стороны треугольника. Примеры применения теоремы:

1. Нахождение отношения длин сторон треугольника:
   Пусть в треугольнике ABC проведены линии DE, EF и FD, и они пересекаются в точке P. Задача состоит в нахождении отношения длин сторон треугольника ABC. Для этого применяем теорему Менелая: AD/DB * BE/EC * CF/FA = 1.
   Известными величинами являются отношения длин сегментов отрезков, а неизвестными являются длины сегментов отрезков.
2. Построение линий: Пусть треугольник ABC задан своими вершинами, и требуется построить линию, проходящую через заданную точку P на стороне AB. Если известны длины отрезков AD, DB, EC и CF, а также известны длины сегментов отрезков, то можно найти длины оставшихся сегментов и построить линию, проходящую через точку P.
3. Нахождение точек пересечения внутренних и внешних биссектрис: Пусть в треугольнике ABC проведены внутренние биссектрисы, которые пересекаются в точке I, и внешние биссектрисы, которые пересекаются в точке I'. Чтобы найти отношения длин отрезков, на которые биссектрисы делят противоположные стороны, можно также использовать теорему Менелая.

Задачи

Решение:

Имеем: DM/BM = (DM/BM+MD) = 2MB/3MB (DM=2MB) = 2/3. То есть DM/BD = 2/3.

Далее CX/XM = (CM-XM)/XM = 1/2 (AC/XM) -1 (AM=MC) = 1/2(3)-1.

(AC/MX=3)=1/2.

То есть CX/XM = 1/2.

Теперь рассмотрим ΔMBC и точки D, X и Y. 

Решение: Обозначим точку пересечения медианы с BC как D. По теореме Менелая для треугольника ABC получаем: AD/DB * BC/CA * AC/AB = 1

Что дано: AD/DB = 2/3.

Подставляя это значение, получаем: (2/3) * BC/CA * AC/AB = 1. Учитывая, что BC/CA = 1 (так как медиана делит сторону BC пополам) и упрощая уравнение, получаем: (2/3) * AC/AB = 1.

AC/AB = 3/2

Отношение длин сторон AB и AC равно 3:2.

Решение: В треугольнике ABC биссектриса делит сторону: AD/DB * BC/CA * AC/AB = 1

Заметим, что точка D — точка пересечения биссектрисы с противоположной стороной. Это значит, что длины отрезков, на которые биссектриса делит угол ACB, равны:
AD/DB = AC/AB.

Таким образом, отрезки AD и BD делят угол ACB пополам.

Решение: В треугольнике ABC, в котором точки пересечения высот делят стороны:

AD/DB * BE/EC * CF/FA = 1.

Точка H является ортоцентром, является точкой пересечения всех трех высот. Это значит, что длины отрезков, на которые высота делит стороны, равны:
AD/DB = BE/EC = CF/FA.

Получим, что точки H делят стороны треугольника в одинаковом отношении.