Локальная и интегральная теоремы Лапласса

Личность Пьер-Симона Лапласа

Пьер-Симон Лаплас известен в качестве ученого из Франции, который изучал и добился высоких результатов в таких научных областях, как математика, механика, физика, астрономия. Популярность исследователю принести труды в области небесной механики, анализ дифференциальных математических соотношений. Лаплас являлся одним из авторов вероятностной теории.

Сложно переоценить заслуги ученого в математических и астрономических дисциплинах. Благодаря исследованиям великого научного деятеля, были качественно доработаны практически все направления перечисленных областей. Пьер-Симон Лаплас состоял во Французском Географическом обществе, шести научных академиях и королевских организациях, в числе которых Академия Петербурга (1802 г). Исследователь заслужено был удостоен звания величайшего ученого Франции. С этим перечнем великих научных деятелей можно ознакомиться при посещении Эйфелевой башни в Париже.

Интегральная теорема Муавра-Лапласа

В процессе разбора теоремы для наглядности приведем простой пример. Предположим, что имеется тысяча деталей. Пусть усредненная концентрация бракованных товаров, которыми нельзя пользоваться, составляет 10%. При этом некорректно сделать вывод о наличии 100 единиц брака в рассматриваемой основной партии, так как записанный процент является средним. Возможно, что некачественных деталей всего 101, 98 или другое число. Вычислить, каковы шансы найти в партии ровно 100 изделий с браком, можно с помощью теоремы Муавра-Лапласа в интегральном виде. Данный подход значительно упрощает и сокращает расчеты.

В данном случае функцию F, которая включена в запись выражения, называют функцией Муавра-Лапласа. Ее расчет построен по такому принципу: \(F\left( x \right)=\frac{2}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\int\limits_{0}^{x}{e}}^{-\frac{{{t}^{2}}}{2}}}dt\)

 

Стоит отметить, что для записи формул используются сокращенные обозначения. К примеру, n обозначает число испытаний, р является вероятностью успешного исхода, q представляет собой вероятность провального опыта и выражается следующим соотношением:

\(q=1-p\)

В данном случае соблюдено следующее условие:

\(\Phi \left( x \right)=\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}\int\limits_{0}^{x}{{{e}^{-\frac{{{t}^{2}}}{2}}}dt}\)

Локальная теорема Муавра-Лапласа

В процессе определения числа m исходов опыта А при общем количестве n по формуле Бернулли в распространенных случаях предстоит вычислить вероятность, с которой m принадлежит некому интервалу а и b. Если n достаточно велико, то значительно усложняется применение биномиального распределения:

\(p_{n}(m)={\frac {n!}{m!(n-m)!}}p^{m}q^{{n-m}}\)

По вышеописанной причине целесообразно прибегнуть к использованию асимптотического соотношения для биномиального распределения. При этом необходимо выполнение условия, при котором р не меняется, а \(n\rightarrow +\infty\). Согласно теореме Муавра — Лапласа подобным выражением служит нормальная функция.

В данном случае:

\(\left|\alpha _{n}(m)\right|<{\frac {c}{\sqrt {n}}},c={\text{const}}>0\)

Заметим, что при условии: n>100 и m>20, целесообразно воспользоваться следующим выражением:

\(P_{n}(m)\approx {\frac {1}{{\sqrt {2\pi npq}}}}\exp \left(-{\frac {x_{m}^{2}}{2}}\right)\)

Таблицы

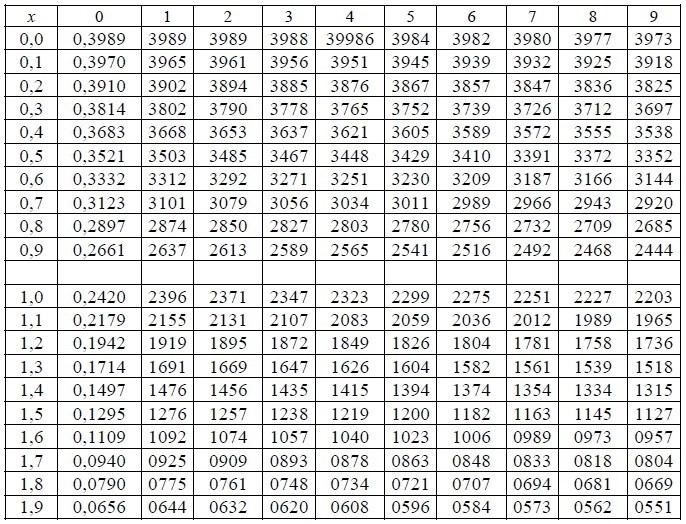
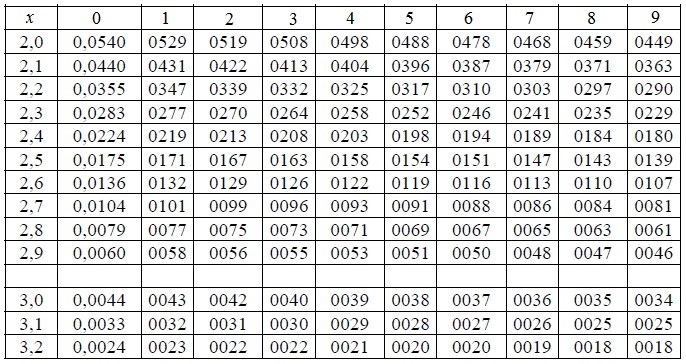
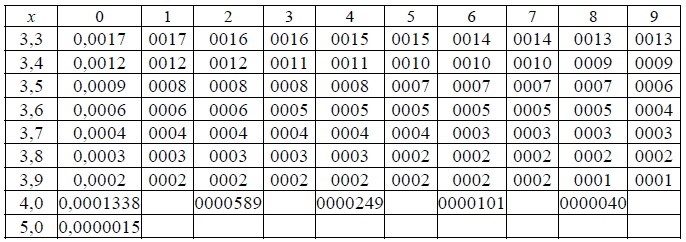
Таблица значений локальной функции Лапласа:

 

 

 

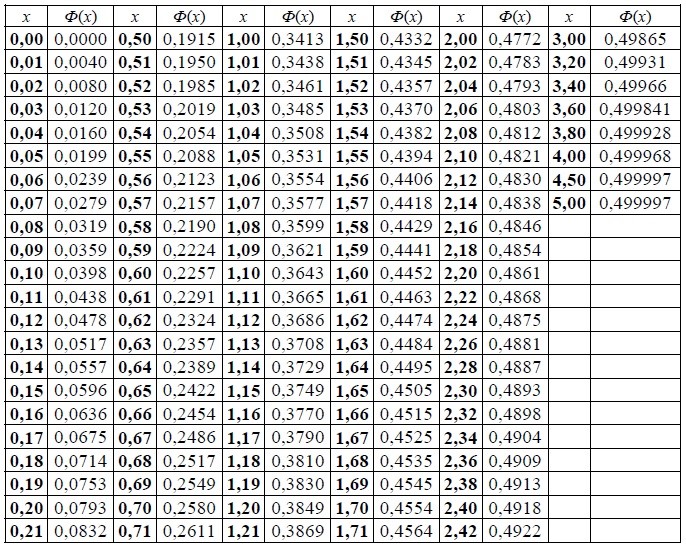
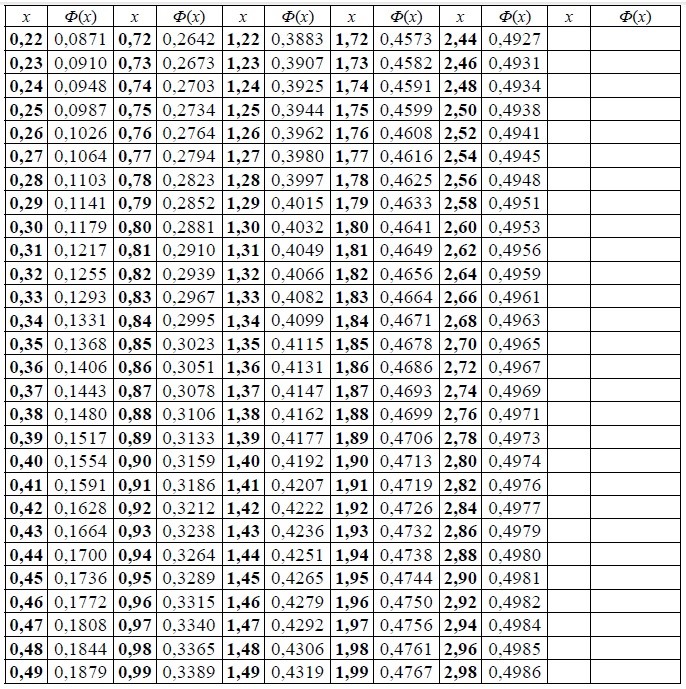
Таблица значений интегральной функции Лапласа:

 

 

Примеры решения задач

Решение

Заметим, что в данном случае целесообразно воспользоваться теоремой Муавра-Лапласа в интегральной форме, то есть:

\({{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-np}{\sqrt{npq}} \right)-F\left( \frac{{{K}_{1}}-np}{\sqrt{npq}} \right)\)

Здесь также целесообразно воспользоваться следующим соотношением, с которым мы уже успели познакомиться в начале темы:

\(F\left( x \right)=\frac{2}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\int\limits_{0}^{x}{e}}^{-\frac{{{t}^{2}}}{2}}}dt\)

Запишем условия задачи, чтобы было удобно выполнять подстановку числовых значений величин в записанную ранее формулу:

n=200

p=0,05

1-0,05=0,95

Далее определим значение \(\sqrt{npq}\):

\(\sqrt{npq}=\sqrt{200\cdot 0,05\cdot 0,95}=\sqrt{9,5}\approx 3,08\)

Затем вычислим, чему равно np:

\(np=200\cdot 0,05=10\)

Путем подстановки продолжим расчет:

\({{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{200-10}{3,08} \right)-F\left( \frac{20-10}{3,08} \right)= F\left( 61,7 \right)-F\left( 3,25 \right)\)

\(F\left( x \right)=\frac{2}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\int\limits_{0}^{x}{e}}^{-\frac{{{t}^{2}}}{2}}}dt\)

\({{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx 0,5-0,49942=0,00058=5,8\cdot {{10}^{-4}}\)

Ответ: \(5,8\cdot {{10}^{-4}}\)

Решение

Запишем данные из условия задачи:

n=1000

\(p=\frac{1}{2}\)

\(q=1-\frac{1}{2}=\frac{1}{2}\)

Воспользуемся рассмотренными ранее формулами и выполним соответствующие вычисления:

\({{P}_{1000}}\left( {{K}_{1}};{{K}_{2}} \right)=0,99\)

Заметим, что при определении интервала значений событий напрашивается следующий вывод:

\({{K}_{1}}=0\)

В таком случае необходимо вычислить, чему соответствует \({K}_{2}\). Обратимся к формулировке теоремы Муавра-Лапласса:

\({{P}_{1000}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-np}{\sqrt{npq}} \right)-F\left( \frac{{{K}_{1}}-np}{\sqrt{npq}} \right)\)

Отметим, что в данном случае справедливым является следующее равенство:

\(np=1000\cdot \frac{1}{2}=500\)

В результате:

\(\sqrt{npq}=\sqrt{1000\cdot \frac{1}{2}\cdot \frac{1}{2}}=\sqrt{250}=5\sqrt{10}=15,8\)

Путем подстановки численных значений, которые были определены ранее, учитывая, что \({K}_{1}=0\), получим следующее соотношение:

\({{P}_{1000}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-500}{15,8} \right)-F\left( \frac{0-500}{15,8} \right)=0,99\)

Рассчитаем значение функции по доказательству:

\(F\left( \frac{-500}{15,8} \right)=-F\left( 31,6 \right)=0,5\)

Таким образом:

\(F\left( \frac{{{K}_{2}}-500}{15,8} \right)+0,5=0,99\)

\(F\left( \frac{{{K}_{2}}-500}{15,8} \right)=+0,49\)

С помощью табличной формы определим близкие к 0,49 значения функции. Таковым соответствуют точки 2,32 и 2,34. Выполним вычисления:

\(F\left( 2,32 \right)=0,48983\)

\(F\left( 2,34 \right)=0,49036\)

\(\frac{{{K}_{2}}-500}{15,8}=2,33\)

\({{K}_{2}}-500=2,33\cdot 15,8\)

\({{K}_{2}}-500=36,8\)

\({{K}_{2}}\approx 536,8=537\)

Ответ: 537.