Таблица основных значений тригонометрических функций

Полная таблица тригонометрических функций

Тригонометрическими называют простейшие функции, возникновение которых связано с историческими фактами. Данные зависимости были сформированы в процессе изучения треугольников, которые обладают одним прямым углом. С их помощью записаны соотношения размеров сторон этих геометрических фигур по отношению к гипотенузе, при которой расположены острые углы.

Функции в тригонометрии используют при решении разнообразных задач. Кроме того, подобные закономерности широко применяют в других областях научных знаний. В процессе пополнения теоретической базы математических данных можно проследить расширение области определений тригонометрических функций. К примеру, в настоящее время роль аргумента рассматриваемых зависимостей может играть какое-либо число из множества вещественных и комплексных.

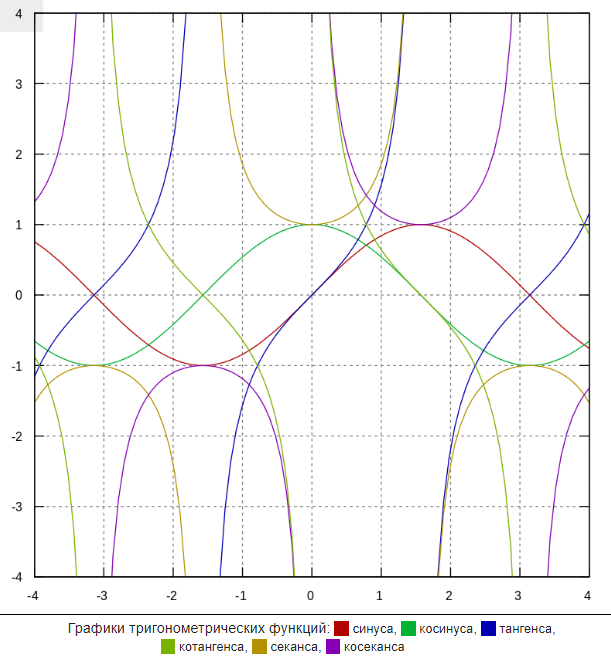
Графики функциональных соотношений в тригонометрии:

 

Источник: ru.wikipedia.org

Перечислим классические тригонометрические функции:

• синус \((\sin x)\);
• косинус \((\cos x)\).

Производными таких зависимостей являются следующие функции:

• тангенс \(\left(\mathrm {tg} \,x={\frac {\sin x}{\cos x}}\right)\);
• котангенс \(\left(\mathrm {ctg} \,x={\frac {\cos x}{\sin x}}\right)\);
• секанс \(\left(\sec x={\frac {1}{\cos x}}\right)\);
• косеканс \(\left(\mathrm {cosec} \,x={\frac {1}{\sin x}}\right)\).

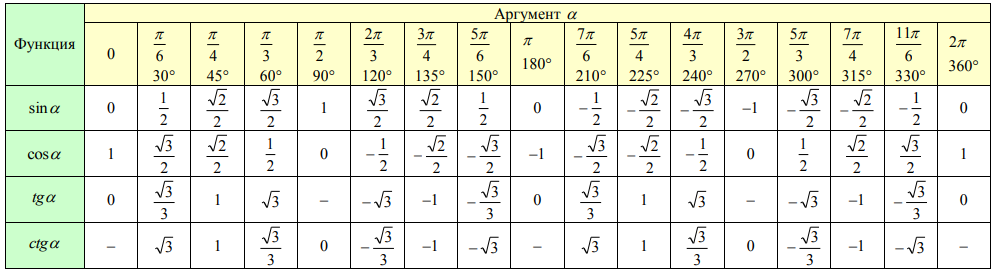
Таблица, включающая в себя значения, которые приобретают тригонометрические соотношения определенных аргументов, выраженных в градусах или радианах:

Источник: www.mathprofi.ru

Заметим, что при наличии прочерка в ячейке можно слать вывод об отсутствии значения для данной функции. В процессе освоения курса тригонометрии нет необходимости учить наизусть представленные выше величины. С целью упрощения решения задач можно запомнить лишь несколько ключевых выражений:

\(\sin 0 = 0\)

\(\sin \frac{\pi}{2} = 1\)

\(\cos 0 = 1\)

\(\cos \frac{\pi}{2} = 0\)

В таблице значения аргумента функции могут быть указаны в градусах и радианах. При решении задач нередко возникает необходимость перевода одних величин в другие. В связи с этим полезно будет узнать, как перевести градусы в радианы, а также запомнить обратную процедуру:

\(\alpha (град.) = \alpha (рад.)\cdot \frac{180}{\pi}\)

Существует и обратное соотношение, благодаря которому получается быстро представить градусную меру угла в радианах. Зависимость данных величин можно описать с помощью такого соотношения:

\(\alpha (рад.) = \frac{\alpha (град.) \cdot \pi}{180} \)

Источник: ru.wikipedia.org

Свойства тригонометрических функций

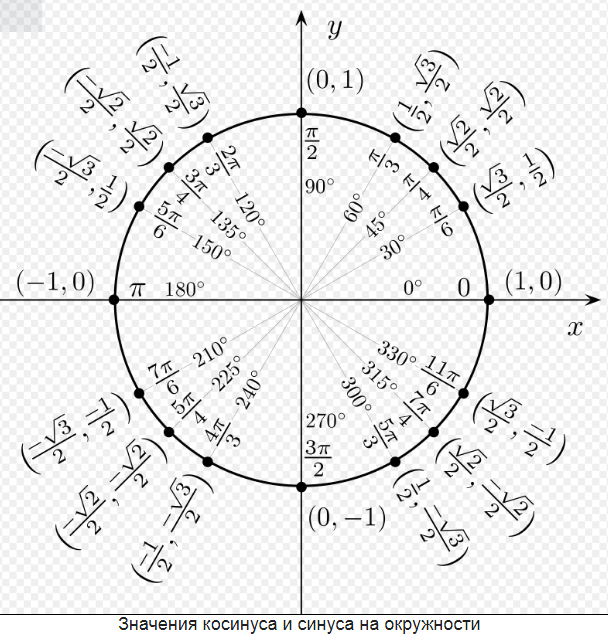
Рассмотрим самые простые тождества, которые удобно применять для решения задач по тригонометрии. Заметим, что синус и косинус представляют собой обозначения ординаты и абсциссы, которые имеет некая точка, отмеченная на единичном круге. Данная точка соответствует углу \(\alpha\). Запишем соотношение, применительно к такой числовой окружности:

\(x^{2}+y^{2}=1\)

Воспользуемся теоремой Пифагора, чтобы выразить взаимосвязь ключевых тригонометрических функций:

\(\sin ^{2}\alpha +\cos ^{2}\alpha =1\)

Данную закономерность называют основным тригонометрическим тождеством.

Путем простых алгебраических преобразований допустимо вывести из него несколько полезных формул. К примеру, поделим полученное равенство на косинус и синус, возведенные во вторую степень. В результате получим следующее:

\(1+\mathop {\mathrm {tg} } \,^{2}\alpha =\mathop {\mathrm {sec} } \,^{2}\alpha\)

\(1+\mathop {\mathrm {ctg} } \,^{2}\alpha =\mathop {\mathrm {cosec} } \,^{2}\alpha\)

Если вспомнить, что обозначают тангенс и котангенс, то основное тождество допустимо записать в таком виде:

\(\mathop{\mathrm{tg}}\,\alpha \cdot \mathop{\mathrm{ctg}}\,\alpha=1\)

В том случае, когда функции тригонометрии обладают одинаковым аргументом, справедливо представить одну такую функцию с помощью другой. Рассмотрим ситуацию, когда \(0<x<\pi /2\) :

\(\sin x= {\sqrt {1-\cos ^{2}x}} = {\frac {\operatorname {tg} x}{\sqrt {1+\operatorname {tg} ^{2}x}}} = {\frac {1}{\sqrt {\operatorname {ctg} ^{2}x+1}}}\)

\(\cos x= {\sqrt {1-\sin ^{2}x}} = {\frac {1}{\sqrt {1+\operatorname {tg} ^{2}x}}} = {\frac {\operatorname {ctg} x}{\sqrt {\operatorname {ctg} ^{2}x+1}}}\)

 

Источник: ru.wikipedia.org

Как пользоваться таблицей

История материалов по исследованию геометрических фигур в виде треугольников прослеживается еще со второго тысячелетия до нашей эры и ранее в Древнем Египте и Вавилоне. Учения из научного направления тригонометрии были обнаружены в Никее. Первооткрывателем тригонометрических законов считают Гиппарха. Известно, что он впервые представил таблицу, которая содержала величины дуг и хорд для определенных углов. Таким образом, по-видимому, появился прототип таблицы тригонометрических следующих функций:

• синус, обозначает соотношение гипотенузы и катета, которые расположен напротив нее;
• косинус, показывает зависимости величины катета, который является прилежащим к гипотенузе;
• тангенс, в виде отношения двух катетов, расположенных напротив друг друга;
• котангенс, отражает, как относится прилежащий катет к противоположному.

Разобраться с таблицей тригонометрических функций не составит труда. Данная табличная форма основана на интуитивно понятном принципе сопоставления значений. В ячейке, которая расположена на пересечении строки и столбца, записано значение той или иной функциональной зависимости.

В качестве примера можно рассмотреть алгоритм действия для определения \(\sin\frac{7\pi}{6} \):

• найти в табличной форме столбец с ячейкой, обладающей значением в \(7\pi\) радиан, то есть 210 градусов;
• определить строчку, в которой перечислены значения синусов углов;
• там, где определенный ранее столбец пересекается со строкой, будет записано нужная величина, то есть: \(\sin\frac{7\pi}{6} = \frac{1}{2}\).