Что нужно знать о суммах углов треугольников — основные сведения

Теорема о сумме углов треугольника является одной из базовых в геометрии. 

Теорема о сумме углов в треугольнике

На протяжении длительного времени другого взгляда не было, в математике XIX века он был единственно правильным. Однако позднее, выяснилось, что в других пространствах (в других геометриях) этот показатель может быть больше либо меньше 180о. Это — следствие случая углового дефекта. В нем состоит отличие между геометрическими системами.

Теорема о сумме углов треугольника справедлива для любого многоугольника, имеющего три вершины:

• остроугольного (имеющего все три острых угла);
• прямоугольного (один угол равен 90о);
• тупоугольного (один из трех углов тупой);
• равнобедренного (две боковые стороны равны. Это катеты. Третья — основание);
• равностороннего (все три стороны имеют равные длины).

Доказательство теоремы о сумме углов треугольника

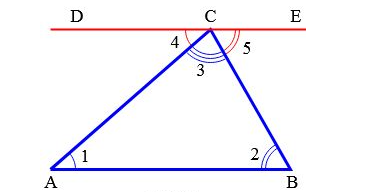
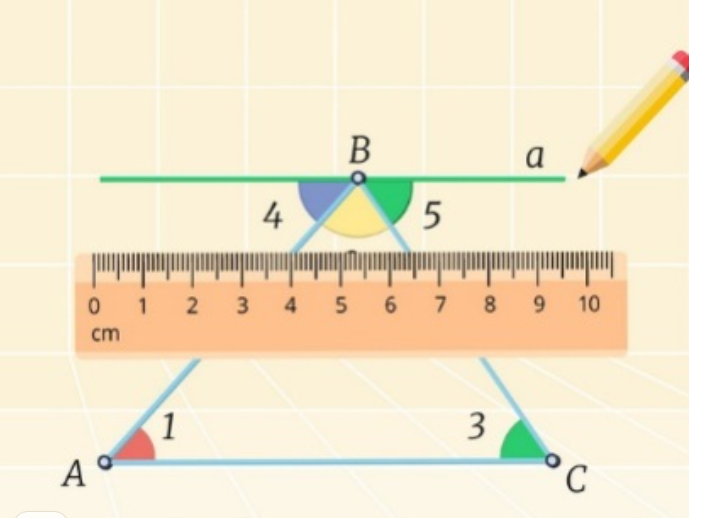
 Рассмотрим чертеж, на котором изображен треугольник ABC . Через одну из вершин проведем прямую a, которая параллельна основанию AC:

Угол 1 равен углу 4. Это утверждение вытекает из свойства параллельных прямых, которое гласит, что углы, образовавшиеся накрест в местах пересечения прямых и секущей (в данной ситуации это прямые a и AC, а секущая — AB) равны.

Аналогичная картина по равенству углов 3 и 5, только секущей является прямая BC.

Следовательно, при сложении углов 4, 2 и 5 согласно признаку развернутого угла получается 180^о. Аналогично по сумме углов 1, 2 и 3.

Приведенные аргументы позволяют сделать вывод, что задача доказана: сумма углов A, B, C составляет 180^о.

Рассмотрим еще одно важное понятие: внешний угол и чему равна его величина. Внешний угол всегда расположен рядом с соответствующим смежным — внутренним углом треугольника.

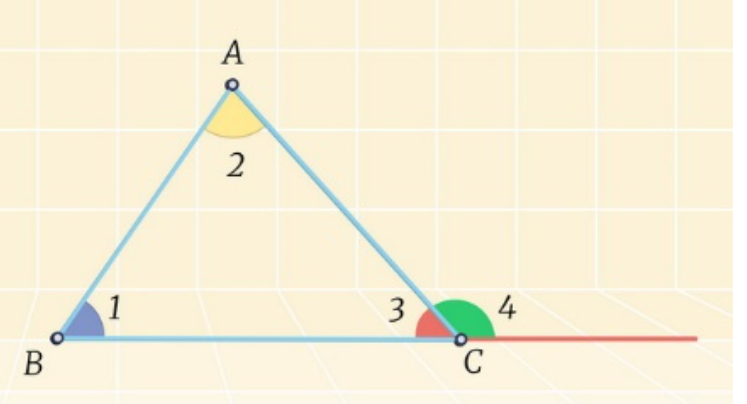
Смоделируем ситуацию с помощью рисунка.

На нем угол 4 является смежным с углом 3. Кроме этого, он равен сумме двух других углов треугольника (1 и 2).

По определению развернутого угла сумма углов 3 и 4 равна 180^о.

Используя теорему о сумме углов в треугольнике, приходим к выводу, что при сложении углов 3 c (угол 1 плюс угол 2) получается 180^о. Это и есть искомое доказательство.

Следствия из теоремы о сумме углов треугольника

Из теоремы о сумме углов треугольника вытекает верное следствие: когда один из трех углов прямой, два других — острые, причем их сумма также равна 90^о.

Аналогичное утверждение справедливо для ситуации, когда один из углов больше 90^о. Тогда два других угла также острые, однако, их сумма менее 90^о.

Общее утверждение: любой треугольник имеет либо все углы острые, либо два острых, а третий равен 90^о либо больше 90^о (угол тупой).

Следствие о сумме острых углов в прямоугольном треугольнике также можно доказать.

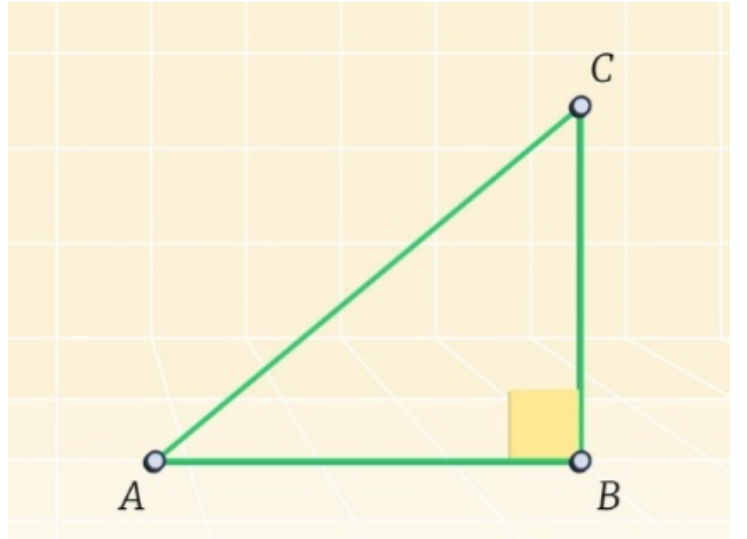
В прямоугольном треугольнике ABC прямым углом является угол B. Глядя на рисунок, докажем, что сумма углов A и C также равна 90^о.

Согласно теореме о сумме углов в треугольнике сумма всех его углов равна 180^о.

A+B+C=180^о.

Известно, что угол B прямой, поэтому справедлива формула: A+C=180^о-B=180^о-90^о=90^о

Примеры решения задач

Задача 1

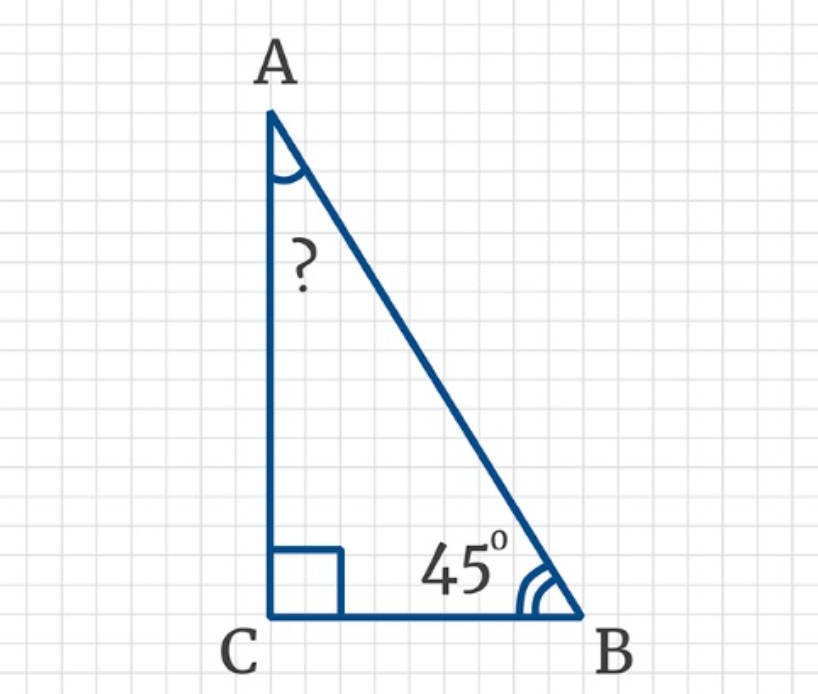
Дан прямоугольный треугольник ABC. Угол C прямой, угол B равен 45о. Сколько градусов составляет угол A?

Решение задачи можно выразить уравнением:

A+B+C=180^о

A=180^о-(B+C)

A=180^о-(90^о+45^о)

A=45^о

Задача 2

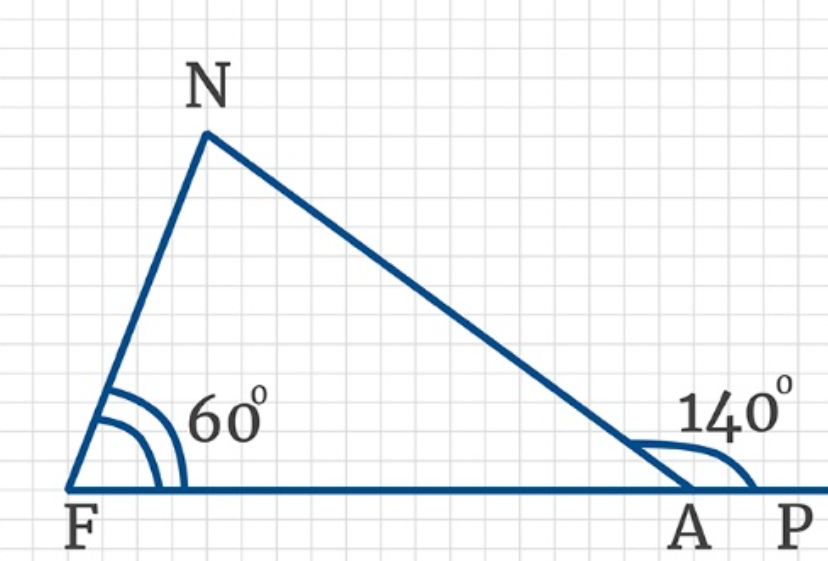
Дан треугольник FNA. Известно, что один из его углов (F) равен 60о. Кроме этого по условию дано, что угол A смежный с углом P, который равен \(140^0\)

Какова градусная мера угла N?

Угол NAP равен 140^о. Он является внешним к углу A в треугольнике FNA.

Угол NAP=угол N+ угол F=140^о такое утверждение справедливо, поскольку внешний угол треугольника равняется сумме оставшихся двух углов треугольника, которые с ним не смежны.

F=60^о

Угол N+60^о=140^о

Угол N=140^о-60^о=80^о