Таблицы интегралов для 11 классов и студентов
Определение интеграла
Интеграл представляет собой одно из ключевых понятий в математическом анализе. С помощью интегралов упрощается вычисление таких величин, как:
- площадь фигуры, расположенной под кривой линией;
- преодоленный путь в процессе неравномерного перемещения;
- масса, которой обладает неоднородное тело.
Благодаря навыку определения интегралов, упрощается решение задач, в том числе, тригонометрических, на восстановление функции при известной ее производной на курсах физики и алгебры. Интеграл справедливо сравнить с суммой для неограниченного количества бесконечно малых слагаемых.
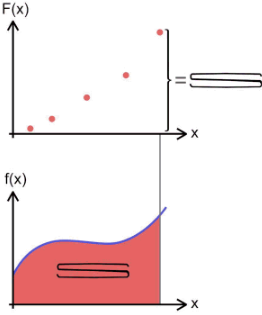
Интеграл является математической концепцией, сформулированной в двух вариантах: неопределенный интеграл, как функция, полученная путем интегрирования, и определенный интеграл в виде выраженной области, расположенной ниже, чем кривая линия, являющаяся графиком неотрицательной функции \(f\), между какой-либо парой значений а и b.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определенный интеграл обозначают таким образом: \(\int_{a}^{b}\).
Неопределенный интеграл записывают следующим способом: \(\int\).
Представим, что имеется какая-то функция действительной переменной. Обозначим ее \(f(x)\). Сформулируем определение неопределенного интеграла.
Неопределенный интеграл функции \(f(x)\), либо ее первообразной, представляет собой функцию \(F(x)\) с производной, равной \(f(x)\), таким образом, что \(F'(x)=f(x)\):
\(F(x)=\int f(x)dx\)
Здесь \(\int\) обозначает интеграл, \( f(x)\) является подынтегральной функцией, dx обозначает элемент интегрирования.
Первообразная предусмотрена не для всех функций. Каждая функция, являющаяся непрерывной, обладает первообразной. В связи с совпадением производных пары функций, которые отличаются на постоянную величину, в соотношение для неопределенного интеграла записывают произвольную константу С, к примеру:
\(\int x^{2}dx={\frac {x^{3}}{3}}+C,\qquad \int \cos(x)dx=\sin(x)+C\)
Вычисление интеграла является действием под названием интегрирование.
Заметим, что интегрирование и дифференцирование представляют собой операции, противоположные друг другу, то есть:
\({\frac {d}{dx}}\int f(x)dx=f(x),\qquad \int {\frac {df(x)}{dx}}dx=f(x)+C\)
Понятие определенного интеграла вытекает из решения примеров на вычисление площади, которой характеризуется криволинейная трапеция, расстояния, исходя из заданной скорости в процессе неравномерного движения, и других подобных задач.
Представим, что имеется некая фигура, которая ограничена осью абсцисс, упирается в прямые \(х = а\) и \(х = b\), имеет границу в виде графика функции \(y=f(x)\). Данная область представляет собой криволинейную трапецию.
В том случае, когда на оси абсцисс отмечено время, а ось ординат отображает скорость тела, площадь криволинейной трапеции справедливо считать расстоянием, которое преодолело тело.
Определить площадь криволинейной трапеции можно в несколько этапов. Вначале потребуется выполнить следующие действия:
- Деление отрезка \([a;b]\) на части с помощью точек \(x_{i}\), при которых \(a=x_{0}<...<x_{i}<x_{i+1}<...<x_{n}=b.\)
- Деление трапеции на определенное количество узких полос, которые расположены над отрезками \([x_{i};x_{i+1}]\).
- Обозначение на каждом из полученных отрезков произвольной точки \(\xi _{i}\in [x_{i};x_{i+1}]\).
При малом значении длины i-го отрезка \(\Delta x_{i}=x_{i+1}-x_{i} \) допустимо принять величину функции \(f(x)\) на нем приблизительно неизменным и соответствующим \(y_{i}=f(\xi _{i})\). Тогда площадь криволинейной трапеции можно считать примерно равной площади полученной ступенчатой фигуры:
\(S\approx \sum _{i=0}^{n-1}y_{i}\Delta x_{i}\)
Площадь ступенчатой фигуры приближается к значению площади криволинейной трапеции, когда увеличивается количество точек разбиения, то есть длины каждого из отрезков без ограничений уменьшаются:
\(\max \Delta x_{i}\to 0\)
Исходя из вышесказанного, можно сформулировать понятие определенного интеграла.
При наличии для любых точек разбиения отрезка и точек \(\xi _{i}\) предела суммы \(S\approx \sum _{i=0}^{n-1}y_{i}\Delta x_{i}\), когда длины всех отрезков стремятся к нулевому значению, данный предел является определенным интегралом от функции \(f(x)\) по отрезку \([a;b]\) и имеет следующее обозначение:
\(\int \limits _{a}^{b}f(x)dx\)
Непосредственно функцию при этом называют интегрируемой на отрезке \([a;b]\). Предусмотрено определение интегральной суммы для таких выражений, как: \(S\approx \sum _{i=0}^{n-1}y_{i}\Delta x_{i}\)
Приведем несколько примеров функций, которые являются интегрируемыми:
- непрерывные;
- обладающие только конечным количеством разрывов первого рода;
- монотонные.
Определенный и неопределенный интегралы связаны между собой. Рассмотрим такое условие:
\(\int f(x)dx=F(x)+C\)
При этом справедливо следующее соотношение:
\(\int \limits _{a}^{b}f(x)dx=F(b)-F(a)\)
Данное выражение является формулой Ньютона-Лейбница.
Общие правила интегрирования функций
Методика непосредственного интегрирования предполагает тождественные преобразования подынтегральной функции, а также использование свойств интеграла для получения одного или нескольких табличных интегралов.
Попробуем вычислить следующий интеграл:
\(\int{\frac{{{x}^{2}}+x\sin x}{x}dx}\)
В первую очередь следует почленно поделить подынтегральную функцию:
\(\int{\frac{{{x}^{2}}+x\sin x}{x}dx}=\int{\left( \frac{{{x}^{2}}}{x}+\frac{x\sin x}{x} \right)dx}=\int{\left( x+\sin x \right)dx}\)
Зная, что интеграл от суммы соответствует сумме интегралов, запишем следующее:
\(\int{\frac{{{x}^{2}}+x\sin x}{x}dx}=\int{xdx}+\int{\sin xdx}\)
В результате получилась сумма, слагаемыми в которой являются табличные интегралы. Таким образом:
\(\int{\frac{{{x}^{2}}+x\sin x}{x}dx}=\frac{{{x}^{2}}}{2}-\cos x+C\)
Запишем окончательный ответ:
\(\int{\frac{{{x}^{2}}+x\sin x}{x}dx} = \frac{{{x}^{2}}}{2}-\cos x+C\)
Следующий способ интегрирования заключается в подведении под знак дифференциала. Данная методика аналогична методу подстановки.
Представим, что:
\(f\left( x \right)=v\left( u\left( x \right) \right)\)
В таком случае, справедливо следующее:
\(\int{f\left( x \right)dx}=\int{v\left( u\left( x \right) \right)}dx\cdot \frac{d\left( u\left( x \right) \right)}{d\left( u\left( x \right) \right)}=\int{v\left( u\left( x \right) \right)}\cdot \frac{d\left( u\left( x \right) \right)}{\frac{d\left( u\left( x \right) \right)}{dx}}=\int{v\left( u\left( x \right) \right)}\cdot \frac{d\left( u\left( x \right) \right)}{{u}'\left( x \right)}\)
Имеется интеграл \(\int{x\sin {{x}^{2}}dx}\), который необходимо определить. Для этого запишем х под знаком дифференциала:
\(xdx=d\left( \frac{{{x}^{2}}}{2} \right)=\frac{1}{2}d\left( {{x}^{2}} \right)\)
В результате:
\(\int{x\sin {{x}^{2}}dx}=\int{\sin {{x}^{2}}\cdot \frac{1}{2}d\left( {{x}^{2}} \right)}=\frac{1}{2}\int{\sin {{x}^{2}}d\left( {{x}^{2}} \right)}\)
Воспользуемся таблицей интегралов и запишем следующее:
\(\int{\sin {t}dt}=-\cos t+C\)
Введем следующее обозначение:
\(t={{x}^{2}}\)
В таком случае, получим:
\(\int{x\sin {{x}^{2}}dx}=\frac{1}{2}\int{\sin {{x}^{2}}d\left( {{x}^{2}} \right)}=\frac{1}{2}\cdot \left( -\cos {{x}^{2}} \right)+C=-\frac{\cos {{x}^{2}}}{2}+C\)
Ответ можно записать таким образом:
\(\int{x\sin {{x}^{2}}dx} = -\frac{\cos {{x}^{2}}}{2}+C\)
Метод замены переменной, или метод подстановки, предусматривает введение новой переменной интегрирования. В процессе требуется записать данный интеграл в виде какого-то нового интеграла, имеющего табличное значение, либо такого интеграла, который можно в дальнейшем привести к табличному виду.
Предположим, что задан интеграл:
\(\int{f\left( x \right)dx}\)
Введем следующее значение и выполним подстановку:
\(x=\phi \left( t \right)\)
В результате, получим:
\(dx={\phi }'\left( t \right)dt \)
Интеграл будет преобразован таким образом:
\(\int{f\left( x \right)dx}=\int{f\left( \phi \left( t \right) \right)\cdot {\phi }'\left( t \right)dt}\)
Требуется вычислить следующий интеграл:
\(\int{\frac{\ln x}{x}dx}\)
Заметим наличие функции и ее производной под знаком интеграла:
\(f\left( x \right)=\ln x\)
\({f}'\left( x \right)={{\left( \ln x \right)}^{\prime }}=\frac{1}{x}\)
Введем обозначение:
\(\ln x=t\)
В таком случае, дифференциал примет вид:
\(\frac{dx}{x}=dt\)
Начальный интеграл можно преобразовать таким образом:
\(\int{\frac{\ln x}{x}dx}=\int{\ln x\cdot \frac{dx}{x}}=\int{tdt}=\frac{{{t}^{2}}}{2}+C\)
Зная, что неопределенный интеграл определяется переменной интегрирования, выполним замену в обратную сторону:
\(t=\ln x\)
В результате:
\(\int{\frac{\ln x}{x}dx}=\frac{{{\ln }^{2}}x}{2}+C\)
Реализация метода интегрирования по частям предполагает использование следующей формулы:
\(\int{udv}=uv-\int{vdu}\)
Вместо представленной формулы можно воспользоваться таким выражением:
\(\int{u\left( x \right){v}'\left( x \right)dx}=u\left( x \right)v\left( x \right)-\int{v\left( x \right){u}'\left( x \right)dx}\)
Важно, что при выполнении вычислений найти интеграл \(\int{vdu}\) значительно проще по сравнению с определением начального интеграла \(\int{udv}\). Лишь при этом условии методика интегрирования по частям имеет смысл.
Рассмотрим реализацию метода на примере следующего интеграла:
\(\int{x\sin xdx}\)
Решим его способом интегрирования по частям:
\(\int{x\sin xdx}\ \left\| \begin{matrix} u=x & dv=\sin xdx \\ du=dx & v=-\cos x \\ \end{matrix} \right\|=x\cdot \left( -\cos x \right)-\int{\left( -\cos x \right)dx}=-x\cos x+\int{\cos xdx}=-x\cos x+\sin x+C\)
Таким образом:
\(\int{x\sin xdx}=-x\cos x+\sin x+C\)
Применение интеграла
Интеграл используют для определения расстояния, которое преодолевает материальная точка. Предположим, что движение точки можно задать некой прямой, совпадающей с осью Ох. Скорость передвижения данной точки известна и меняется. Движение на каком-то интервале \(\left[ {{t}_{1}};\ {{t}_{2}} \right]\) можно описать с помощью следующей закономерности:
\(v=v\left( t \right)\)
В результате путь вычисляется таким образом:
\(S=\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{v\left( t \right)dt}\)
Некая материальная точка пребывает в движении и имеет скорость \(v\left( t \right)={{t}^{2}}+1.\) За время \(\left[ 0;\ 1 \right]\) секунды точка преодолела какое-то расстояние, которое нужно вычислить. Для этого воспользуемся интегралом и запишем формулу пути:
\(S=\int\limits_{0}^{1}{\left( {{t}^{2}}+1 \right)dt}=\left. \left( \frac{{{t}^{3}}}{3}+t \right) \right|_{0}^{1}=\frac{{{1}^{3}}}{3}+1-\left( \frac{{{0}^{3}}}{3}+0 \right)=\frac{1}{3}+1=\frac{4}{3}\)
В результате:
\(S=\frac{4}{3}\)
Используя интегралы, достаточно просто описать связь между работой и силой. Например, совершается некая работа А в процессе движения материальной точки под воздействием силы F от значения \({{x}_{1}}\) к значению \({{x}_{2}}\) закономерность описана соотношением:
\(A=\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{F\left( x \right)dx}\)
Рассматриваемая материальная точка движется в некотором интервале от 1 до 2 метров, благодаря воздействию силы \(F\left( x \right)=x+3\). Нужно вычислить, какая работа при этом производится. Для этого найдем работу А по записанной ранее формуле:
\(A=\int\limits_{1}^{2}{\left( x+3 \right)dx}=\left. \left( \frac{{{x}^{2}}}{2}+3x \right) \right|_{1}^{2}=\frac{{{2}^{2}}}{2}+3\cdot 2-\left( \frac{{{1}^{2}}}{2}+3\cdot 1 \right)=2+6-\frac{1}{2}-3=\frac{9}{2}\)
Таким образом:
\(A=\frac{9}{2}.\)
Следующим способом применения интеграла является вычисление работы. Представим, что мощность изменяется по определенному закону \(N\left( t \right)\). Тогда в период времени от \( {{t}_{1}} \) до \({{t}_{2}}\) работа А равна:
\(A=\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{N\left( t \right)dt}\)
В течение временного периода \(\left[ 1;\ 4 \right]\) изменение мощности можно описать такой закономерностью:
\(N\left( t \right)=\frac{6}{\sqrt{t}}\)
Требуется определить, чему при этом равна работа А. Для этого воспользуемся уже знакомой формулой:
\(A=\left. \int\limits_{1}^{4}{\frac{6dt}{\sqrt{t}}}=6\cdot 2\sqrt{t} \right|_{1}^{4}=12\cdot \left( \sqrt{4}-\sqrt{1} \right)=12\cdot \left( 2-1 \right)=12\)
В результате:
\(A=12\)
С применением интеграла упрощается вычисление массы тонкого стержня. Данная величина m при известной линейной плотности стержня \(\rho \left( x \right)\) определяется следующим образом:
\(m=\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\rho \left( x \right)dx}\)
Часть стержня обладает некоторой массой, которую требуется вычислить, от значений \({{x}_{1}}=0 \) до \({{x}_{2}}=1\) с учетом линейной плотности, равной:
\(\rho \left( x \right)={{x}^{2}}+1\)
Воспользуемся формулой, записанной ранее:
\(m=\int\limits_{0}^{1}{\left( {{x}^{2}}+1 \right)dx}=\left. \left( \frac{{{x}^{3}}}{3}+x \right) \right|_{0}^{1}=\frac{{{1}^{3}}}{3}+1-\left( \frac{{{0}^{3}}}{3}+3 \right)=\frac{4}{3}\)
В таком случае:
\(m=\frac{4}{3}\)
Умение вычислять интегралы обязательно пригодится для расчета количества электричества, то есть электрического заряда. Данная величина за временной интервал \(\left[ {{t}_{1}};\ {{t}_{2}} \right]\), когда известна сила тока \(I=I\left( t \right)\), определяется следующим соотношением:
\(q=\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{I\left( t \right)dt} \)
В течение временного интервала \(\left[ 3;\ 4 \right]\) проводник проводит ток силой \(I\left( t \right)=3{{t}^{2}}-2t\) в количестве, которое требуется вычислить. Воспользуемся записанной формулой:
\(q\left. =\int\limits_{3}^{4}{\left( 3{{t}^{2}}-2t \right)dt}=\left( {{t}^{3}}-{{t}^{2}} \right) \right|_{3}^{4}={{4}^{3}}-{{4}^{2}}-\left( {{3}^{3}}-{{3}^{2}} \right)=64-16-27+9=30\)
Тогда:
\(q=30\)
С помощью интеграла достаточно просто рассчитать количество теплоты за определенное время. При этом требуется знать теплоемкость \(c\left( t \right)\) и время \(t\in \left[ {{t}_{1}};\ {{t}_{2}} \right]\). Тогда справедлива следующая формула:
\(Q=\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{c\left( t \right)dt}\)
В течение времени \(t\in \left[ 1;\ 2 \right]\) выделена теплота, количество которой нужно определить при теплоемкости \( c\left( t \right)={{t}^{2}}\). Воспользуемся подходящей формулой:
\(Q=\int\limits_{1}^{2}{{{t}^{2}}dt}=\left. \frac{{{t}^{3}}}{3} \right|_{1}^{2}=\frac{{{2}^{3}}-{{1}^{3}}}{3}=\frac{7}{3}\)
В таком случае:
\(Q=\frac{7}{3}.\)
Интегралом выражают связь между магнитным потоком \(\Phi \) и электродвижущей силой. Если индукция равна \({{\varepsilon }_{i}}\left( t \right)\), то зависимость этих величин в контуре можно описать следующим соотношением:
\(\Phi =\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{{{\varepsilon }_{i}}\left( t \right)dt}\)
Представим, что рамка вращается в однородном магнитном поле. В результате такого движения формируется ЭДС индукции, временные изменения которой можно описать закономерностью:
\({{\varepsilon }_{i}}\left( t \right)=50\cos \frac{\pi t}{120}\)
Требуется определить величину магнитного потока, который проходит через рамку в конце первой минуты вращения.
В этом случае целесообразно принять время t в виде изменения от 0 с до 60 с. Тогда необходимый электромагнитный поток равен:
\(\Phi =\int\limits_{0}^{60}{50\cos \frac{\pi t}{120}dt}=50\cdot \frac{120}{\pi }\sin \left. \frac{\pi t}{120} \right|_{0}^{60}=\frac{600}{\pi }\left( \sin \frac{\pi }{2}-\sin 0 \right)=\frac{600}{\pi }\)
В результате:
\(\Phi =\frac{600}{\pi}\)
Используя интеграл, вычисляют площадь S криволинейной трапеции по формуле:
\(S=\int\limits_{a}^{b}{f\left( x \right)dx}\)
Дана криволинейная трапеция, которая ограничена графиком \(y=4x-{{x}^{2}}, x=0, x=4\) и осью абсцисс. Требуется вычислить, чему равна ее площадь. Воспользуемся записанной формулой:
\(S=\int\limits_{0}^{4}{\left( 4x-{{x}^{2}} \right)dx}=\left. \left( 2{{x}^{2}}-\frac{{{x}^{3}}}{3} \right) \right|_{0}^{4}=2\cdot {{4}^{2}}-\frac{{{4}^{3}}}{3}-\left( 2\cdot {{0}^{2}}-\frac{{{0}^{3}}}{3} \right)=32-\frac{64}{3}=\frac{32}{3}\)
В результате:
\(S=\frac{32}{3}\)
Рассмотрим следующий способ применения интеграла, который состоит в определении длины дуги плоской кривой. Представим, что в прямоугольной системе координат задана некоторая плоская кривая AB, соответствующая уравнению:
\(y=f\left( x \right),\ a\le x\le b\)
В том случае, когда функция \(y=f\left( x \right)\) и ее производная \({y}'={f}'\left( x \right)\) не прерываются на интервале \(\left[ a;\ b \right]\) длина кривой AB равна:
\(l=\int\limits_{a}^{b}{\sqrt{1+{{\left( {f}'\left( x \right) \right)}^{2}}}dx}\)
Центр окружности совпадает с началом координат и имеет радиус R. Требуется рассчитать длину заданной окружности. Запишем уравнение окружности:
\({{x}^{2}}+{{y}^{2}}={{R}^{2}}\)
В таком случае:
\(y=\pm \sqrt{{{R}^{2}}-{{x}^{2}}}\)
Если рассмотреть тот сектор окружности, который расположен в первой четверти \((y\ge 0)\), то можно записать следующее:
\(y=\sqrt{{{R}^{2}}-{{x}^{2}}}\)
Заметим, что длина \({{l}_{1}} \) данной четверти в 4 раза меньше по сравнению с общей длиной l:
\(l=4{{l}_{1}}\)
Вычислим подынтегральную функцию \(\sqrt{1+{{\left( {f}'\left( x \right) \right)}^{2}}}\):
\(y=\sqrt{{{R}^{2}}-{{x}^{2}}}\Rightarrow {y}'=\frac{-2x}{2\sqrt{{{R}^{2}}-{{x}^{2}}}}=\frac{-x}{\sqrt{{{R}^{2}}-{{x}^{2}}}}\)
\(\sqrt{1+{{\left( {f}'\left( x \right) \right)}^{2}}}=\sqrt{1+{{\left( -\frac{x}{\sqrt{{{R}^{2}}-{{x}^{2}}}} \right)}^{2}}}=\sqrt{1+\frac{{{x}^{2}}}{{{R}^{2}}-{{x}^{2}}}}=\sqrt{\frac{{{R}^{2}}}{{{R}^{2}}-{{x}^{2}}}}=\frac{R}{\sqrt{{{R}^{2}}-{{x}^{2}}}}\)
Изменения переменной в первой четверти соответствует от 0 до R. Вычислим длину:
\(l=4\int\limits_{0}^{R}{\frac{Rdx}{\sqrt{{{R}^{2}}-{{x}^{2}}}}}=\left. 4R\cdot \arcsin \frac{x}{R} \right|_{0}^{R}=4R\cdot \left( \arcsin 1-\arcsin 0 \right)=4R\cdot \frac{\pi }{2}=2\pi R\)
В результате:
\(l=2\pi R\)
С помощью интегралов вычисляют объем тела вращения. Предположим, что вокруг оси \(Ох\) вращается какая-то криволинейная трапеция. Фигура ограничена непрерывной линией \(y=f\left( x \right)\), прямыми \(x=a\) и \(x=b\). В результате такого движения получается тело вращения, объем которого можно вычислить по формуле:
\({{V}_{Ox}}=\pi \int\limits_{a}^{b}{{{y}^{2}}dx}\)
В том случае, когда криволинейная трапеция ограничена графиком непрерывающейся функции \(x=g\left( y \right)\) и прямыми \(y=c\) и \(y=d\), объем тела вращения составляет:
\({{V}_{Oy}}=\pi \int\limits_{a}^{b}{{{x}^{2}}dy}\)
Некая фигура ограничена линиями \(y=\frac{{{x}^{2}}}{2}, x=0 \) и \(y=2\sqrt{2}\). Данная фигура совершает вращательное движение вокруг оси ординат. Необходимо определить объем тела вращения. Для этого воспользуемся формулой:
\({{V}_{Oy}}=\pi \int\limits_{0}^{2\sqrt{2}}{{{x}^{2}}dy}\ \left\| \begin{matrix}y=\frac{{{x}^{2}}}{2}\Rightarrow\\{{x}^{2}}=2y\\\end{matrix} \right\|=\pi \left. \int\limits_{0}^{2\sqrt{2}}{2ydy}=\pi \cdot {{y}^{2}} \right|_{0}^{2\sqrt{2}}=\pi \cdot \left( {{\left( 2\sqrt{2} \right)}^{2}}-{{0}^{2}} \right)=8\pi\)
Получим, что:
\({{V}_{Oy}}=8\pi\)
Интеграл целесообразно использовать, когда требуется определить площадь поверхности вращения. К примеру, имеется прямая \(АВ\), заданная функцией \(y=f\left( x \right)\ge 0,\ x\in \left[ a;\ b \right]\). Данная функция не прерывается вместе со своей производной \({y}'\left( x \right)\) на рассматриваемом отрезке. Площадь S поверхности, которая является результатом вращения кривой \(AB\) вокруг оси \(Ox\), определяется таким образом:
\({{S}_{Ox}}=2\pi \int\limits_{a}^{b}{y\sqrt{1+{{\left( {y}'\left( x \right) \right)}^{2}}}dx}\)
Необходимо вычислить площадь поверхности шара, центр которого совпадает с началом координат, а радиус равен R. Представим, что поверхность шара является результатом вращательного движения некой полуокружности \(y=\sqrt{{{R}^{2}}-{{x}^{2}}}\), \(-R\le x\le R\) относительно оси абсцисс. Вычислим нужную площадь:
\({{S}_{Ox}}=2\pi \int\limits_{a}^{b}{\sqrt{{{R}^{2}}-{{x}^{2}}}\sqrt{1+{{\left( {{\left( \sqrt{{{R}^{2}}-{{x}^{2}}} \right)}^{\prime }} \right)}^{2}}}dx}=2\pi \int\limits_{a}^{b}{\sqrt{{{R}^{2}}-{{x}^{2}}}\sqrt{1+{{\left( \frac{-x}{\sqrt{{{R}^{2}}-{{x}^{2}}}} \right)}^{2}}}dx}=2\pi \int\limits_{a}^{b}{\sqrt{{{R}^{2}}-{{x}^{2}}+{{x}^{2}}}dx}=2\pi R\left. \int\limits_{a}^{b}{dx}=2\pi R\cdot x \right|_{-R}^{R}=2\pi R\left( R-\left( -R \right) \right)=4\pi {{R}^{2}}\)
В результате:
\({{S}_{Ox}}=4\pi {{R}^{2}}\)
Свойства определенного интеграла
Рассмотрим ключевые свойства определенного интеграла. К примеру, отсутствует зависимость между определенным интегралом и переменной интегрирования:
\(\int\limits_{a}^{b}{f\left( x \right)dx}=\int\limits_{a}^{b}{f\left( t \right)dt}=\int\limits_{a}^{b}{f\left( y \right)dy}\)
При равных пределах интегрирования определенного интеграла его значение равно нулю:
\(\int\limits_{a}^{a}{f\left( x \right)dx}=0\)
В том случае, когда подынтегральная функция соответствует следующему выражению: \(f\left( x \right)=C=\text{const}\), определенный интеграл от рассматриваемой функции по промежутку \(\left[ a;\ b \right]\) вычисляется, как произведение константы C на длину промежутка \(b-a\):
\(\int\limits_{a}^{b}{C\cdot dx}=C\left( b-a \right)\)
Допустимо выносить за знак определенного интеграла множитель, который является постоянным:
\(\int\limits_{a}^{b}{Cf\left(x \right)dx}=C\int\limits_{a}^{b}{f\left(x\right)dx}\)
Интеграл от суммы интегрированных на промежутке \(\left[ a;\ b \right]\) функций вычисляется, как результат сложения интегралов от каждой из этих функций:
\(\int\limits_{a}^{b}{\left[ {{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)+...+{{f}_{n}}\left( x \right) \right]dx}=\int\limits_{a}^{b}{{{f}_{1}}\left( x \right)dx}+\int\limits_{a}^{b}{{{f}_{2}}\left( x \right)dx}+...+\int\limits_{a}^{b}{{{f}_{n}}\left( x \right)dx}\)
При смене мест пределов интегрирования знак определенного интеграла меняется на противоположный:
\(\int\limits_{a}^{b}{f\left( x \right)dx}=-\int\limits_{b}^{a}{f\left( x \right)dx}\)
В том случае, когда функция \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\) является интегрируемой на интервале \(\left[ a;\ b \right]\), при условии, что \(c\in \left( a;\ b \right)\), справедливо следующее соотношение:
\(\int\limits_{a}^{b}{f\left( x \right)dx}=\int\limits_{a}^{c}{f\left( x \right)dx}+\int\limits_{c}^{b}{f\left( x \right)dx}\)
Теорема про среднее: когда функция \(y=f\left( x \right)\) является интегрируемой на промежутке \( \left[ a;\ b \right]\), имеется такая точка \(\xi \in \left[ a;\ b \right]\), что справедливо следующее выражение:
\(\int\limits_{a}^{b}{f\left( x \right)dx}=f\left( \xi \right)\left( b-a \right)\)
В том случае, когда функция \(y=f\left( x \right)x = {-b \pm \sqrt{b^2-4ac} \over 2a}\) не меняет знак на конкретном отрезке \(\left[ a;\ b \right]\), определенный интеграл \(\int\limits_{a}^{b}{f\left( x \right)dx}\) обладает таким же знаком на данном промежутке, что и подынтегральная функция.
При условии, что:
\({{f}_{1}}\left( x \right)\le {{f}_{2}}\left( x \right),\ x\in \left[ a;\ b \right]\)
справедливо следующее равенство:
\(\int\limits_{a}^{b}{{{f}_{1}}\left( x \right)dx}\le \int\limits_{a}^{b}{{{f}_{2}}\left( x \right)dx}.\)
В том случае, когда функция \(y=f\left( x \right)\) принимает на промежутке \(\left[ a;\ b \right]\) свои минимальное m и максимальное M значения, справедливы следующие неравенства:
\(m\left( b-a \right)\le \int\limits_{a}^{b}{f\left( x \right)dx}\le M\left( b-a \right).\)
Модуль определенного интеграла не может быть больше, чем интеграл от модуля подынтегральной функции:
\(\left| \int\limits_{a}^{b}{f\left( x \right)dx} \right|\le \int\limits_{a}^{b}{\left| f\left( x \right) \right|dx}.\)
Производная от интеграла, который имеет изменяющийся верхний предел, соответствует величине подынтегральной функции от данного предела:
\({{\left( \int\limits_{a}^{x}{f\left( t \right)dt} \right)}^{\prime }}=f\left( x \right).\)
Предположим, что функция \(y=f\left( x \right)\) не прерывается на промежутке \(\left[ -a;\ a \right]\), который симметричен по отношению к точке \(x=0\). В таком случае верным является следующее соотношение:
\(\int\limits_{-a}^{a}{f\left( x \right)dx}=\left\{ \begin{matrix}& 0,\ f\left( x \right) \\ & 2\int\limits_{0}^{a}{f\left( x \right)dx},\ f\left( x \right) \\ \end{matrix} \right.\)
где при \(0 f\left( x \right)\) нечетная, а при \(2\int\limits_{0}^{a}{f\left( x \right)dx},\ f\left( x \right)\) является четной.
Интеграл от периодической с периодом T функции \(y=f\left( x \right)\) обладает одинаковыми значениями на каком-либо отрезке длины T:
\(\int\limits_{0}^{T}{f\left( x \right)dx}=\int\limits_{-T}^{0}{f\left( x \right)dx}=\int\limits_{-\frac{T}{2}}^{\frac{T}{2}}{f\left( x \right)dx}.\)
Неопределенный интеграл и его определение
Разберем свойства неопределенных интегралов. К примеру, допустимо исключать константу из-под знака интеграла:
\(\int{kf\left( x \right)dx}=k\cdot \int{f\left( x \right)dx}\)
Исходя из записанного свойства, вычислим интеграл:
\(\int{4{{x}^{2}}dx}\)
Получим, что:
\(\int{4{{x}^{2}}dx}=4\cdot \int{{{x}^{2}}dx}=4\cdot \frac{{{x}^{3}}}{3}+C=\frac{4{{x}^{3}}}{3}+C\)
Следующее свойство неопределенного интеграла можно сформулировать, как «интеграл суммы или разности равен сумме или разности интегралов от каждого из слагаемых», то есть:
\(\int{\left[ f\left( x \right)\pm g\left( x \right) \right]dx}=\int{f\left( x \right)dx}\pm \int{g\left( x \right)dx}\)
Требуется определить, чему равен интеграл:
\(\int{\left( x+\sin x \right)}dx\)
Воспользуемся записанным свойством:
\(\int{\left( x+\sin x \right)}dx=\int{xdx}+\int{\sin xdx}\)
\(\int{\left( x+\sin x \right)}dx=\frac{{{x}^{2}}}{2}-\cos x+C\)
Производная от интеграла определяется, как подынтегральная функция:
\({{\left( \int{f\left( x \right)dx} \right)}^{\prime }}=f\left( x \right)\)
Нужно вычислить интеграл:
\({{\left( \int{{{x}^{2}}dx} \right)}^{\prime }}\)
Согласно записанному свойству, получим:
\({{\left( \int{{{x}^{2}}dx} \right)}^{\prime }}={{x}^{2}}\)
Интеграл от дифференциала функции соответствует сумме данной функции и постоянной интегрирования:
\(\int{df\left( x \right)dx}=f\left( x \right)+C\)
Необходимо вычислить значение следующего интеграла:
\(\int{d\left( \arcsin x \right)dx}\)
Воспользуемся уже знакомым свойством:
\(\int{d\left( \arcsin x \right)dx}=\arcsin x+C\)
Другое свойство неопределенного интеграла предполагает, что при условии \(\int{f\left( x \right)dx}=F\left( x \right)+C\) справедливо следующее равенство:
\(\int{f\left( kx+b \right)dx}=\frac{1}{k}F\left( kx+b \right)+C\)
Требуется определить значение интеграла \(\int{3\cdot {{\left( 2x-4 \right)}^{2}}dx}\) при условии, что:
\(\int{3{{x}^{2}}dx}={{x}^{3}}+C.\)
Исходя из записанного свойства, для \(k=2\) верным является следующее соотношение:
\(\int{3\cdot {{\left( 2x-4 \right)}^{2}}dx}=\frac{1}{2}{{\left( 2x-4 \right)}^{3}}+C=\frac{{{\left( 2x-4 \right)}^{3}}}{2}+C\)
Определить интеграл от производной какой-либо функции можно путем сложения данной функции с постоянной интегрирования:
\(\int{{F}'\left( x \right)dx}=F\left( x \right)+C\)
Дано выражение, которое нужно доказать:
\(\int{{{\left( {{x}^{2}} \right)}^{\prime }}dx}={{x}^{2}}+C\)
Определим интеграл \(\int{{{( {{x}^{2}} )}^{\prime }}dx}\). Заметим, что производная подынтегральной функции соответствует следующему значению:
\({{\left( {{x}^{2}} \right)}^{\prime }}=2x\)
В результате:
\(\int{{{\left( {{x}^{2}} \right)}^{\prime }}dx}=\int{2xdx}\)
Воспользуемся свойствами интеграла для вынесения постоянной за знак интеграла:
\(\int{{{\left( {{x}^{2}} \right)}^{\prime }}dx}=2\int{xdx}\)
В таком случае:
\(\int{{{\left( {{x}^{2}} \right)}^{\prime }}dx}=2\int{xdx}=2\cdot \frac{{{x}^{2}}}{2}+C={{x}^{2}}+C\)
\(\int{{{\left( {{x}^{2}} \right)}^{\prime }}dx}={{x}^{2}}+C\)
Соотношение доказано.
Примеры решения задач
Дан интеграл, который требуется вычислить:
\(\int{\left( 6{{x}^{5}}+\frac{2}{x}-\frac{2}{\sqrt{1-{{x}^{2}}}} \right)dx}\)
Решение
Преобразуем начальный интеграл, чтобы получить в итоге сумму интегралов:
\(\int{\left( 6{{x}^{5}}+\frac{2}{x}-\frac{2}{\sqrt{1-{{x}^{2}}}} \right)dx}=\int{6{{x}^{5}}dx}+\int{\frac{2}{x}dx}-\int{\frac{2}{\sqrt{1-{{x}^{2}}}}dx}\)
Постоянные можно вынести за знак интеграла:
\(\int{\left( 6{{x}^{5}}+\frac{2}{x}-\frac{2}{\sqrt{1-{{x}^{2}}}} \right)dx}=6\int{{{x}^{5}}dx}+2\int{\frac{dx}{x}}-2\int{\frac{dx}{\sqrt{1-{{x}^{2}}}}}\)
Подставим значения их таблицы интегралов:
\(\int{\left( 6{{x}^{5}}+\frac{2}{x}-\frac{2}{\sqrt{1-{{x}^{2}}}} \right)dx}=6\cdot \frac{{{x}^{6}}}{6}+2\cdot \ln \left| x \right|-2\arcsin x+C={{x}^{6}}+2\cdot \ln \left| x \right|-2\arcsin x+C\)
Ответ: \(\int{\left( 6{{x}^{5}}+\frac{2}{x}-\frac{2}{\sqrt{1-{{x}^{2}}}} \right)dx} = {{x}^{6}}+2\cdot \ln \left| x \right|-2\arcsin x+C\)
Требуется вычислить следующий интеграл:
\(\int{{{\left( {{x}^{2}}+\sqrt{x} \right)}^{2}}dx}\)
Решение
Рассмотрим подынтегральную функцию. Заметим, что здесь целесообразно воспользоваться формулой сокращенного умножения, то есть квадратом суммы:
\(\int{{{\left( {{x}^{2}}+\sqrt{x} \right)}^{2}}dx}=\int{\left[ {{\left( {{x}^{2}} \right)}^{2}}+2\cdot {{x}^{2}}\cdot \sqrt{x}+{{\left( \sqrt{x} \right)}^{2}} \right]dx}=\int{\left( {{x}^{4}}+2{{x}^{^{\frac{5}{2}}}}+x \right)dx}=\int{{{x}^{4}}dx}+\int{2{{x}^{^{\frac{5}{2}}}}dx}+\int{xdx}=\frac{{{x}^{5}}}{5}+2\cdot \frac{{{x}^{^{\frac{7}{2}}}}}{\frac{7}{2}}+\frac{{{x}^{2}}}{2}+C=\frac{{{x}^{5}}}{5}+\frac{4}{7}\sqrt{{{x}^{7}}}+\frac{{{x}^{2}}}{2}+C\)
Ответ: \(x = \int{{{\left( {{x}^{2}}+\sqrt{x} \right)}^{2}}dx}=\frac{{{x}^{5}}}{5}+\frac{4}{7}\sqrt{{{x}^{7}}}+\frac{{{x}^{2}}}{2}+C.\)
Необходимо найти, чему равен интеграл:
\(\int{{{e}^{2x}}dx}\)
Решение
Введем следующее обозначение:
\(2x=t\)
Путем дифференцирования обеих частей выражения получим, что:
\(d\left( 2x \right)=d\left( t \right) \text{ } \Rightarrow \text{ } 2dx=dt \text{ } \Rightarrow \text{ } dx=\frac{dt}{2}\)
Путем подстановки полученного выражения преобразуем начальный интеграл:
\(\int{{{e}^{2x}}dx}=\int{{{e}^{t}}\cdot \frac{dt}{2}}=\frac{1}{2}\int{{{e}^{t}}dt}\)
В результате получился интеграл из таблицы:
\(\int{{{e}^{2x}}dx}=\frac{1}{2}{{e}^{t}}+C\)
Путем обратной замены получим:
\(t=2x\)
\(\int{{{e}^{2x}}dx}=\frac{1}{2}{{e}^{2x}}+C\)
Ответ: \(\int{{{e}^{2x}}dx} = \frac{1}{2}{{e}^{2x}}+C.\)
Нужно вычислить интеграл:
\(\int{x\sqrt{x-1}dx}\)
Решение
Введем следующее дополнительное обозначение:
\(x-1={{t}^{2}}\)
\(x={{t}^{2}}+1\)
\(dx=2tdt.\)
Преобразуем начальный интеграл:
\(\int{x\sqrt{x-1}dx}=\int{\left( {{t}^{2}}+1 \right)\sqrt{{{t}^{2}}}\cdot 2tdt}=2\int{{{t}^{2}}\left( {{t}^{2}}+1 \right)dt}=2\int{\left( {{t}^{4}}+{{t}^{2}} \right)dt}=2\int{{{t}^{4}}dt}+2\int{{{t}^{2}}dt}=2\cdot \frac{{{t}^{5}}}{5}+2\cdot \frac{{{t}^{3}}}{3}+C=\frac{2{{t}^{5}}}{5}+\frac{2{{t}^{3}}}{3}+C\ \left\| \begin{matrix} t^{2}=x-1 \Rightarrow\\ t=\sqrt{x-1} \\\end{matrix} \right\|=\frac{2{{\left( \sqrt{x-1} \right)}^{5}}}{5}+\frac{2{{\left( \sqrt{x-1} \right)}^{3}}}{3}+C=\frac{2\sqrt{{{\left( x-1 \right)}^{5}}}}{5}+\frac{2\sqrt{{{\left( x-1 \right)}^{3}}}}{3}+C\)
Ответ: \( \int{x\sqrt{x-1}dx}=\frac{2\sqrt{{{\left( x-1 \right)}^{5}}}}{5}+\frac{2\sqrt{{{\left( x-1 \right)}^{3}}}}{3}+C.\)
Необходимо определить значение интеграла:
\(\int{x\ln xdx}\)
Решение
Заменим u на \(\ln x\). Остальные значения соответствуют dv. В таком случае:
\(\int{x\ln xdx}\ \left\| \begin{matrix} u=\ln x & dv=xdx \\ du=\frac{dx}{x} & v=\frac{{{x}^{2}}}{2} \\\end{matrix} \right\|=\ln x\cdot \frac{{{x}^{2}}}{2}-\int{\frac{{{x}^{2}}}{2}\cdot \frac{dx}{x}}=\frac{{{x}^{2}}\ln x}{2}-\frac{1}{2}\int{xdx}=\frac{{{x}^{2}}\ln x}{2}-\frac{1}{2}\cdot \frac{{{x}^{2}}}{2}+C=\frac{{{x}^{2}}\ln x}{2}-\frac{{{x}^{2}}}{4}+C\)
Ответ: \(\int{x\ln xdx} = \frac{{{x}^{2}}\ln x}{2}-\frac{{{x}^{2}}}{4}+C.\)
Необходимо вычислить значение интеграла:
\(\int{{{e}^{3x}}\cos 3xdx}\)
Решение
Примем за u постоянную. Тогда получим менее сложное выражение:
\(\int{{{e}^{3x}}\cos 3xdx}\ \left\| \begin{matrix} u={{e}^{3x}} & dv=\cos 3xdx \\du=3{{e}^{3x}}dx & v=\frac{\sin 3x}{3} \\\end{matrix} \right\|={{e}^{3x}}\cdot \frac{\sin 3x}{3}-\int{\frac{\sin 3x}{3}\cdot 3{{e}^{3x}}dx}=\frac{{{e}^{3x}}\sin 3x}{3}-\int{{{e}^{3x}}\sin 3xdx}\)
В результате полученный интеграл можно вычислить путем интегрирования по частям. За u обозначим функцию \( {{e}^{3x}}:\)
\(\underline{\int{{{e}^{3x}}\cos 3xdx}}=\frac{{{e}^{3x}}\sin 3x}{3}-\int{{{e}^{3x}}\sin 3xdx}\ \left\|\begin{matrix} u={{e}^{3x}} & dv=\sin 3xdx\\ du=3{{e}^{3x}}dx & v=-\frac{\cos 3x}{3}\\\end{matrix} \right\|=\frac{{{e}^{3x}}\sin 3x}{3}-\left( {{e}^{3x}}\cdot \left( -\frac{\cos 3x}{3} \right)-\int{\left( -\frac{\cos 3x}{3} \right)\cdot 3{{e}^{3x}}dx} \right)=\underline {\frac{{{e}^{3x}}\sin 3x}{3}+\frac{{{e}^{3x}}\cos 3x}{3}-\int{{{e}^{3x}}\cos 3xdx}}\)
Следует записать интегральное равенство:
\(\int{{{e}^{3x}}\cos 3xdx}=\frac{{{e}^{3x}}\left( \sin 3x+\cos 3x \right)}{3}-\int{{{e}^{3x}}\cos 3xdx}+C\)
Решим полученное элементарное выражение:
\(\int{{{e}^{3x}}\cos 3xdx}+\int{{{e}^{3x}}\cos 3xdx}=\frac{{{e}^{3x}}\left( \sin 3x+\cos 3x \right)}{3}\)
\(2\int{{{e}^{3x}}\cos 3xdx}=\frac{{{e}^{3x}}\left( \sin 3x+\cos 3x \right)}{3}\)
Дополним соотношение постоянной интегрирования:
\(\int{{{e}^{3x}}\cos 3xdx}=\frac{{{e}^{3x}}\left( \sin 3x+\cos 3x \right)}{6}+C\)
Ответ: \(\int{{{e}^{3x}}\cos 3xdx} = \frac{{{e}^{3x}}\left( \sin 3x+\cos 3x \right)}{6}+C. \)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так