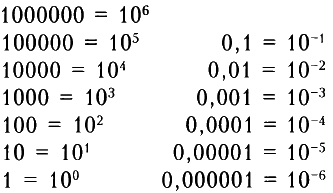Возведение чисел в степень — виды таблиц
Что такое степень числа в математике — основные понятия
Степень в алгебре и информатике — это выражение, которое записано в виде:
\({{a}^{b}}\),
где a обозначает основание степени, а b играет роль ее показателя, который может быть квадратом, в том числе.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Записанную информацию следует читать, как: «а в степени b».
Таким образом, показатель степени b обозначает количество раз, в течение которых число а умножают само на себя.
Требуется возвести число 2 в третью степень. Тогда запишем 2 в степени 3:
\(2^{3} = 2\cdot 2 \cdot 2\)
В данном случае 2 является основанием степени, число 3 обозначает показатель степени.
Перечислим несколько принципов, которые следует учитывать при решении задач со степенями:
- Если отрицательное число возвести в четную степень, то получится положительное число.
- Если отрицательное число возвести в нечетную степень, то получится число со знаком минус.
- При возведении положительного число в какую-либо степень результатом является положительное число.
- Ноль при возведении в какую-либо степень дает ноль.
- При возведении какого-либо числа в нулевую степень получается единица.
Степень с целым показателем является такой степенью, показатель которой записан в виде натурального числа, то есть целого или положительного числа.
Степень с рациональным показателем представляет собой степень с показателем, имеющим знак минус или записанным в виде дробного числа.
Степень с иррациональным показателем — это такая степень, которая имеет на месте показателя бесконечную десятичную дробь или корень.
Возведение в степень, основные свойства
Возведение в степень представляет собой арифметическое действие в виде итога множественного умножения числа самого на себя.
Обозначают степень, основание которой равно а, и натуральный показатель составляет b, таким образом:
\(a^{b}=\underbrace {a\cdot a\cdot \ldots \cdot a} _{b}\),
где b — число множителей, то есть умножаемых чисел.
Запишем несколько степеней для примера:
\(3^{2}=3\cdot 3=9\)
\(2^{4}=2\cdot 2\cdot 2\cdot 2=16\)
Существуют ключевые свойства, которые распространяют свое действие на операции возведения в степень чисел из множества натуральных, целых, рациональных и вещественных. При этом если требуется возвести в степень комплексное число, то показатель должен быть натуральным. Перечислим эти свойства:
- \(a^{1}=a\)
- \(\left(ab\right)^{n}=a^{n}b^{n}\)
- \(\left({a \over b}\right)^{n}={{a^{n}} \over {b^{n}}}\)
- \(a^{n}a^{m}=a^{n+m}\)
- \(\left.{a^{n} \over {a^{m}}}\right.=a^{n-m}\)
- \(\left(a^{n}\right)^{m}=a^{nm}.\)
Следует отметить, что выражение \(a^{n^{m}}\) лишено свойства ассоциативности (сочетательности). Таким образом, в общем случае:
\( (a^{n})^{m}\neq a^{\left({n^{m}}\right)}\)
\((2^{2})^{3}=4^{3}=64\)
\(2^{\left({2^{3}}\right)}=2^{8}=256\)
В процессе решения математических задач данные записи можно считать равнозначными:
\(a^{n^{m}}\)
\(a^{\left({n^{m}}\right)}\)
Руководствуясь записанным свойством, допустимо упростить запись:
\((a^{n})^{m}\)
\(a^{nm}.\)
Операция возведения в степень не характеризуется свойством коммутативности (переместительности):
\(a^{b}\neq b^{a}\)
\(2^{5}=32\)
\(5^{2}=25.\)
Виды таблиц
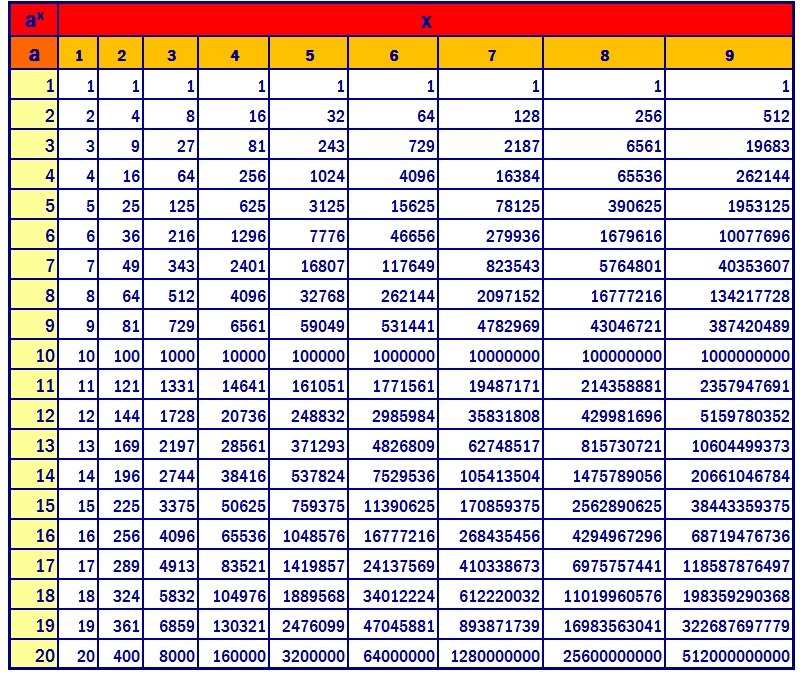
Таблица степеней натуральных чисел:
Таблица отрицательных степеней:
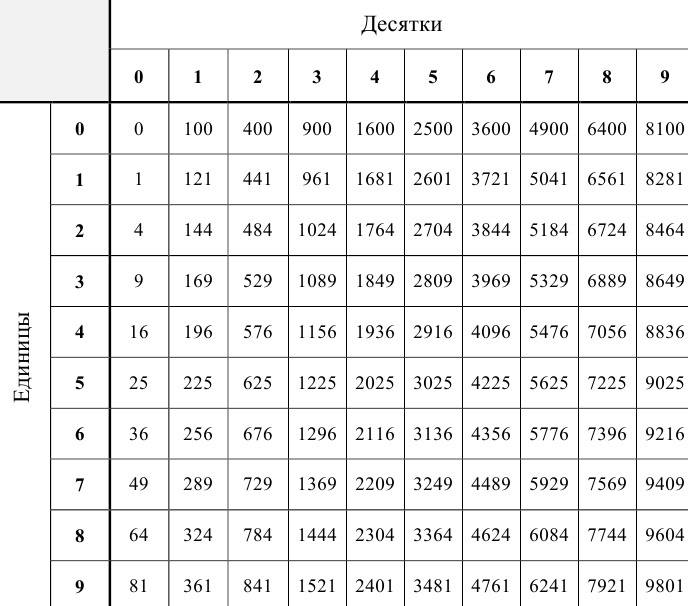
Таблица степеней двузначных чисел:
Примеры решения задач
Дано выражение, значение которого требуется определить:
\({{3}^{7}}+{{5}^{6}}-{{9}^{4}}\)
Решение
С помощью таблицы вычислим значения всех компонентов выражения:
\({{3}^{7}}=2187\)
\({{5}^{6}}=15625\)
\({{9}^{4}}=6561\)
Путем подстановки преобразуем начальное выражение:
\({{3}^{7}}+{{5}^{6}}-{{9}^{4}}=2187+15625-6561=11251\)
Ответ: \({{3}^{7}}+{{5}^{6}}-{{9}^{4}}=11251.\)
Необходимо определить степень, в которую следует возвести число 8 для получения в результате числа 32768.
Решение
По таблице степеней определим:
\({{8}^{5}}=32768\)
Таким образом, нужная степень равна 5.
Ответ: 5.
Дано выражение, значение которого требуется вычислить:
\(\frac{(4^3)^{-4}}{4^{-11}}\)
Решение
Зная, что возведение степени в степень заключается в необходимости умножения показателей этих степеней, преобразуем числитель:
\( (4^3)^{-4} = 4^{-12}\)
В результате:
\(\frac{(4^3)^{-4}}{4^{-11}}=\frac{4^{-12}}{4^{-11}}=4^{-12-(-11)}=4^{-1}=\frac{1}{4}=0,25\)
Ответ: 0,25.
Требуется вычислить значение выражения:
\(6^{-8} \cdot (6^2)^3\)
Решение
В процессе возведения степени в степень необходимо найти произведение показателей этих степеней. Заметим так же, что при умножении степеней, которые имеют идентичные основания, показатели суммируют. Выполним соответствующие преобразования:
\(6^{-8} \cdot (6^2)^3 = 6^{-8} \cdot 6^6 = 6^{-8+6}=6^{-2} = \frac{1}{36}\)
Ответ: \(\frac{1}{36}.\)
Дано выражение, значение которого необходимо вычислить:
\(5^{12} \cdot (5^5)^{-3}\)
Решение
Воспользуемся свойствами степени и выполним соответствующие преобразования:
\(5^{12} \cdot (5^5)^{-3} = 5^{15} \cdot 5^{-15} = 5^{12-15}=5^{-3} = \frac{1}{5^3} = \frac{1}{125}\)
Ответ: \( \frac{1}{125}.\)
Необходимо рассчитать значение следующего выражения:
\(\frac{2^{2} \cdot 8^{-2}}{2^{-5}}\)
Решение
Каждую из степеней требуется привести к основанию в виде числа 2:
\(8^{-2} = {(2^3)}^{-2} = 2^{-6}\)
В результате:
\(\frac{2^{2} \cdot 8^{-2}}{2^{-5}} = \frac{2^{2} \cdot 2^{-6}}{2^{-5}} = 2^{2-6-(-5)} = 2^{1} = 2\)
Ответ: 2.
Нужно найти значение следующего выражения:
\(\frac{5^{6} }{25^{3}\cdot 5^{-2}}\)
Решение
Следует привести каждую из представленных степеней к основанию 5:
\(25^{3} = {(5^2)}^{3} = 5^{6}\)
Таким образом:
\(\frac{5^{6} }{25^{3}\cdot 5^{-2}} = \frac{5^{6} }{5^{6}\cdot 5^{-2}} = 5^{6-6-(-2)}=5^2=25\)
Ответ: 25.
Дано выражение, значение которого нужно вычислить:
\(\frac{l^{6} \cdot {(l^{2})}^{-2}}{l^{-3}}\)
Решение
Заметим, что в процессе возведения степени в степень требуется найти произведение показателей этих степеней:
\({(l^{2})}^{-2} = l^{-4}\)
В результате:
\(\frac{l^{6} \cdot {(l^{2})}^{-2}}{l^{-3}} = \frac{l^{6} \cdot l^{-4}}{l^{-3}} = l^{6-4-(-3)}=l^{5}\)
Ответ: \( l^{5}.\)
Необходимо определить значение такого выражения:
\(\frac{p^{4} \cdot {(p^{2})}^{-3}}{p^{-5} \cdot p^{3}}\)
Решение
Возвести степень в степень можно путем умножения их показателей:
\({(p^{2})}^{-3} = p^{-6}\)
В результате:
\(\frac{p^{4} \cdot {(p^{2})}^{-3}}{p^{-5} \cdot p^{3}} = \frac{p^{4} \cdot p^{-6}}{p^{-5} \cdot p^{3}} = p^{4-6-(-5)-3}=p^{0}=1\)
Ответ: 1.
Дано несколько чисел, среди которых требуется выбрать самое большое:
\(2,5 \cdot 10^{-5}\)
\(1,05 \cdot 10^{-3}\)
\(0,1 \cdot 10^{-3}\)
Решение
Преобразуем перечисленные выражения так, чтобы привести их к виду:
\(a \cdot 10^{-6}\)
В результате:
\(2,5 \cdot 10^{-5} = 2, 5 \cdot 10 \cdot 10^{-6} = 25 \cdot 10^{-6},\)
\(0,1 \cdot 10^{-3}= 0,1 \cdot 10^3 \cdot 10^{-6} = 100 \cdot 10^{-6},\)
\(1,05 \cdot 10^{-3} = 1,05 \cdot 10^3 \cdot 10^{-6} =1050 \cdot 10^{-6}.\)
При сравнении чисел со знаком плюс справедливо, что:
\(a < b\)
\(ac < bc\)
В таком случае целесообразно сравнить множители перед \(\cdot 10^{-6}\). Тогда наибольшим является число \(1,05 \cdot 10^{-3}\).
Ответ: \(1,05 \cdot 10^{-3}.\)
Необходимо выбрать наименьшее число из представленных:
\(1,9 \cdot 10^{-3};\)
\(4,2 \cdot 10^{-5};\)
\(2,2 \cdot 10^{-4};\)
\(2 \cdot 10^{-4}.\)
Решение
Преобразуем перечисленные выражения путем приведения к виду a \(\cdot 10^{-5}:\)
\(1,9 \cdot 10^{-3} = 1,9 \cdot 10^2 \cdot 10^{-5} = 190 \cdot 10^{-5}\)
\(2,2 \cdot 10^{-4}= 2,2 \cdot 10 \cdot 10^{-5} = 22 \cdot 10^{-5}\)
\(2 \cdot 10^{-4} = 2 \cdot 10 \cdot 10^{-5} =20 \cdot 10^{-5}\)
Тогда, наименьшим является число \(4,2 \cdot 10^{-5}.\)
Ответ: \(4,2 \cdot 10^{-5}.\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так