Формулы производных функций: таблица полная

Что такое производная

В процессе решения задач по алгебре можно часто встретить примеры с производными функции. На первый взгляд, подобные задания характеризуются повышенным уровнем сложности. Однако при детальном рассмотрении с решением проблем не возникает. В этом случае важно проанализировать процесс вычислений, сформулировать алгоритм действий, что позволит исключить ошибки в дальнейших расчетах. Знакомство с темой в математике стоит начать с терминологии.

С целью вычисления производной необходимо рассчитать предел отношения увеличения функции к приращению ее аргумента, когда это приращение стремится принять нулевое значение, при условии существования такого предела. Если какая-либо функция обладает окончательной производной в некой точке, то такая функция является дифференцируемой в заданной точке. Когда процесс расчетов заключается в поиске значения производной, действия называют дифференцированием. Обратная операция представляет собой интегрирование. При этом цель задачи заключается в вычислении первообразной.

Источник: ru.wikipedia.org

Рассмотрим порядок действий и принципы нахождения производной. Предположим, что какой-либо области, где расположена точка \(x_{0}\in \mathbb{R}\), определена следующая функция:

\(f\colon U(x_{0})\subset \mathbb{R} \to \mathbb{R}\)

Сформулируем с учетом специфики дифференцирования понятие производной функции. Получается, что это некоторое число А, при котором  функцию в окрестности \(U(x_{0})\) допустимо записать при существовании А с помощью следующего математического соотношения:

\(f(x_{0}+h)=f(x_{0})+Ah+o(h)\)

Существует еще одна расшифровка производной функции. В данном случае используется понятие и правило предела. Представим, что какой-то области точки \(x_{0}\in \mathbb{R}\) обладает определением функция:

\(f\colon U(x_{0})\subset \mathbb{R} \to \mathbb{R}\)

В описанной ситуации производная считается следующим образом:

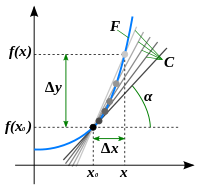
\({ f'(x_{0})=\lim \limits _{x\to x_{0}}{\frac {f(x)-f(x_{0})}{x-x_{0}}}=\lim _{\Delta x\to 0}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}=\lim \limits _{{\Delta x}\to 0}{\frac {\Delta {f(x)}}{\Delta x}}.}\)

Нередко в задачах встречаются такие условия исчислений, при которых наиболее целесообразно использовать обобщенную формулу для расчета производной:

\(f'(x_{0})=f'_{x}(x_{0})={\mathrm {D}}\!f(x_{0})={\frac {df}{dx}}(x_{0})=\left.{\frac {dy}{dx}}\right\vert _{{x=x_{0}}}={\dot {y}}(x_{0}).\)

Свойства производных

Когда известно понятие производной и ряд полезных уравнений для ее вычисления, можно приступать к решению задач. Однако процесс расчетов допустимо упростить. В этом поможет ряд свойств, характерных для производной функции. С помощью простых закономерностей получается сократить алгоритм вычислений и значительно упростить задачу. Рассмотрим основные из них:

1. Вынесение константы за знак производной: \((\alpha*f(x))^{/}=\alpha*(f(x))^{/}.\)
2. Производная от сложения и вычитания пары функций: \((f(x) \pm g(x))^{/}=(f(x))^{/} \pm (g(x))^{/}.\)
3. Производная от умножения пары функций: \((f(x)*g(x))^{/}=(f(x))^{/}*g(x)+f(x)*(g(x))^{/}.\)
4. Производная от деления пары функций: \(\left(\frac{f(x)}{g(x)}\right)^{/}=\frac{(f(x))^{/}*g(x)-f(x)*(g(x))^{/}}{(g(x))^2}.\)

Для чего нужна таблица производных функций, как пользоваться

В решении задач пригодится таблица производных. Используя удобную в работе табличную формулу, можно достаточно быстро отыскать ответ к тому или иному примеру. Подобный подход эффективен на практике, так как позволяет существенно сэкономить время на выполнение вычислений. С другой стороны, таблица содержит в себе справедливые математические соотношения, распространяющиеся на элементарные функции.

По этой причине сначала нужно проанализировать условия задания, преобразовать пример к простому виду с помощью записанных ранее формул и свойств производных. В результате упрощенное выражение достаточно просто отыскать в таблице, чтобы подставить в итоговое соотношение и записать ответ к задаче. Рассмотрим типичные практические примеры.

Решение

Проанализируем задание. Заметим, что речь идет об элементарной функции, производную которой легко найти по табличной форме. Подставим табличное значение в вычисления и запишем ответ:

у' = - sin х

Ответ: у' = - sin х

Формулы производных функций: таблица

Источник: ru.wikipedia.org

Применительно к таблице необходимо принимать во внимание следующие условия:

\({\displaystyle \left(c\right)=\left(\mathrm {const} \right)}\)

\(\left(e^{{x}}\right)^{{\left(n\right)}}=e^{{x}}\)

\({\displaystyle (\ln {x})^{(n)}={\dfrac {(-1)^{n-1}(n-1)!}{x^{n}}}}\)