Подробная таблица косинусов углов

Таблица косинусов в радианах

В радианах принято измерять плоские углы.

Проанализируем данное определение. Заметим, что справедливым является вывод о величине в 2 \(\pi\) радиан, характерной для полного угла.

При решении задач по тригонометрии и геометрии часто приходится иметь дело с углами, измеряемыми в радианах. Упростить вычисление величин можно, если воспользоваться таблицей косинусов углов, для которых известна радианная мера. Кроме того, радианы нередко присутствуют в заданиях по различным темам математического анализа.

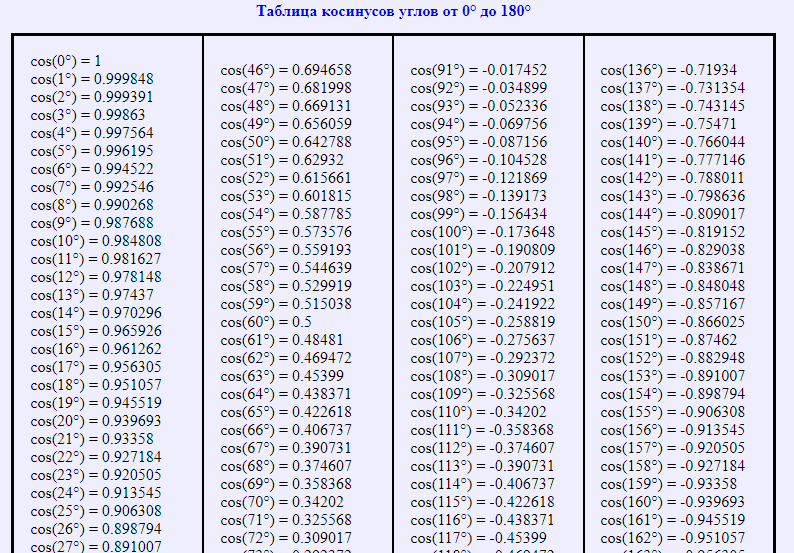
Таблица косинусов от 0° до 180°

Градусы, минуты и секунды являются общеизвестными измерительными единицами, предусмотренными для плоских углов. Угол в 360° соответствует одному полному обороту.

Градусы допустимо выражать в радианах и наоборот. Этот прием полезен для упрощения вычислений при решении задач с плоскими углами. Запишем справедливое соотношение, которое выражает зависимость между данными угловыми мерами:

\(1^{\circ }={\frac {2\pi }{\displaystyle {360}}} радиан ={\frac {\pi }{\displaystyle {180}}}={\frac {1}{\displaystyle {p}}}\approx {\frac {1}{\displaystyle {57{,}295779513^{\circ }}}}{\displaystyle \approx 0{,}0174532925}\)

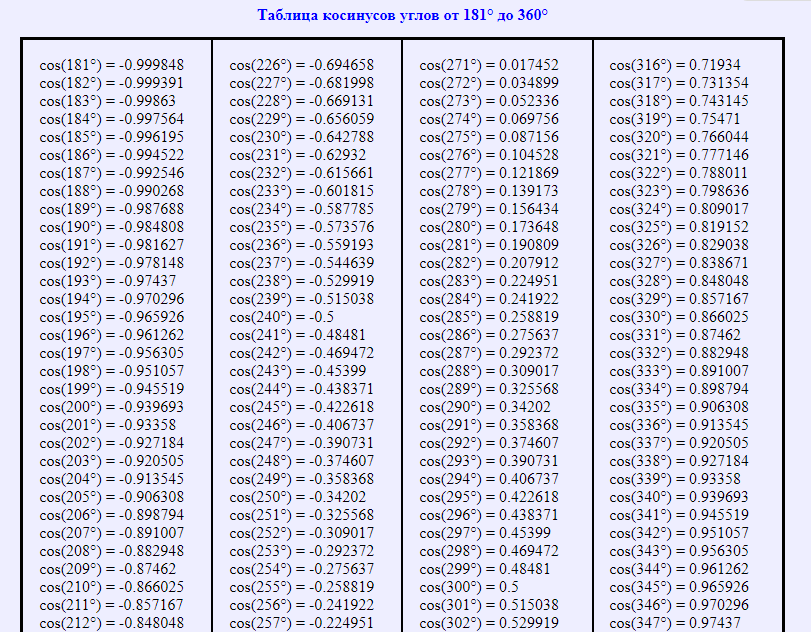
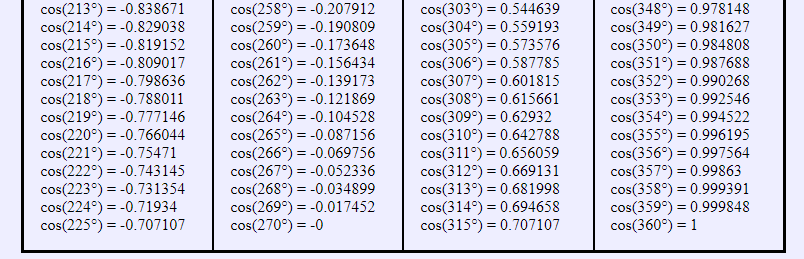
Таблица косинусов от 181° до 360°

В геометрических задачах принято вычислять тригонометрические функции, характерные для острого угла, по соотношениям сторон, которыми обладает прямоугольный треугольник. Предположим, что имеется некий треугольник АОВ с прямым углом. Обозначим в нем за гипотенузу сторону ОВ, а для острого угла запишем следующее равенство:

\(\angle AOB=\alpha\)

При таких исходных данных косинус можно вычислить по формуле:

\(\cos \alpha ={\frac {OA}{OB}}\)

Однако не во всех случаях вышеуказанное соотношение подходит для проведения вычислений. Значительно упростить решение тригонометрических задач можно, если воспользоваться таблицей косинусов:

Как пользоваться таблицей

Таблица, в которой собраны значения косинусов для углов от 0° до 360°, либо углов, выраженных в радианной мере, является информационным материалом, который используют математики и физики. С помощью данного справочного пособия удается упростить и сократить решения разных задач по алгебре, геометрии, физике, математическому анализу, тригонометрии и другим дисциплинам, где приходится часто сталкиваться с массивными вычислениями.

Пользоваться рассматриваемой таблицей достаточно просто. Стандартный алгоритм действий ее применения в решении примеров состоит в выполнении нескольких ключевых операций:

• выявить тригонометрическую функцию в математическом соотношении;
• при необходимости требуется привести функцию к табличной форме;
• найти по таблице значение косинуса;
• путем подстановки известной величины продолжить математические преобразования и вычисления.