Тригонометрическая таблица тангенсов и котангенсов
Таблица тангенсов и котангенсов
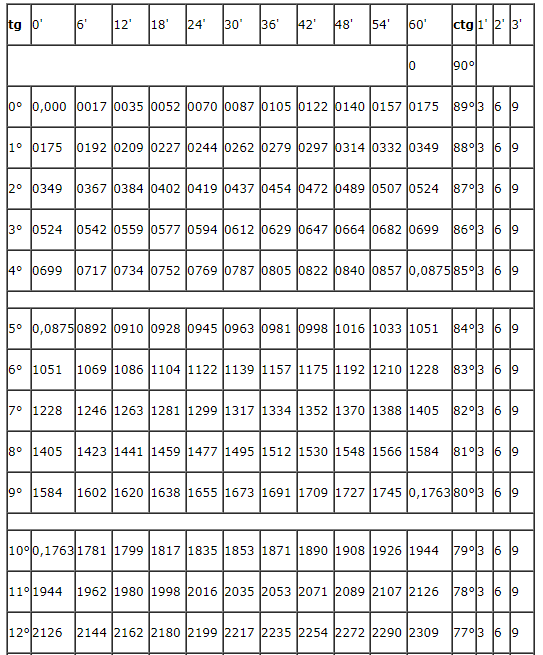
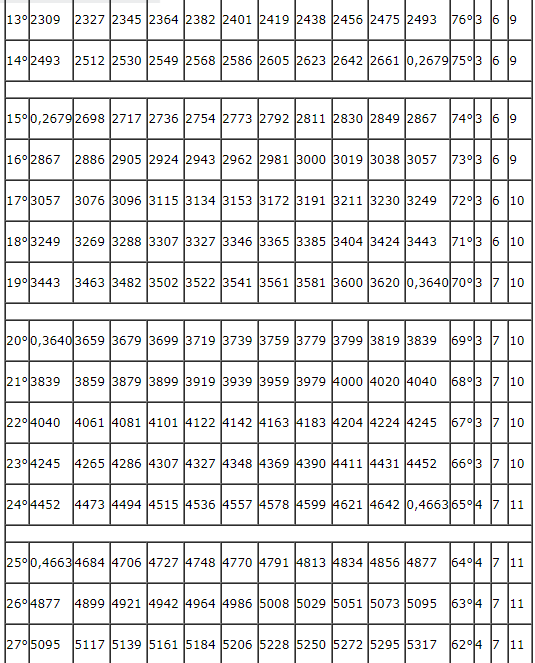
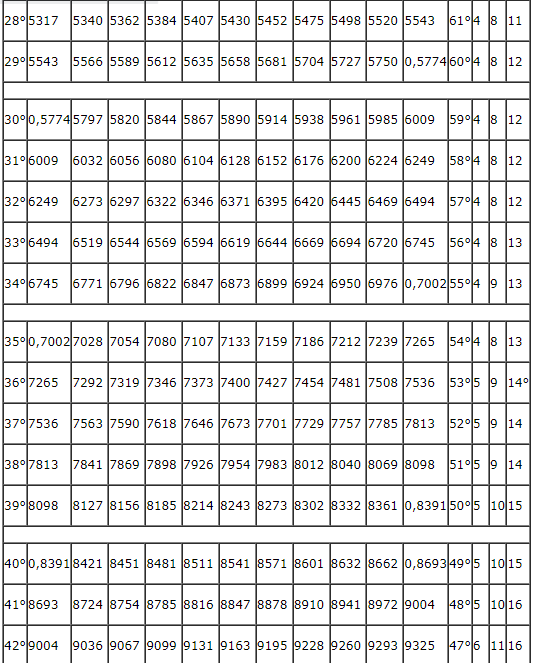
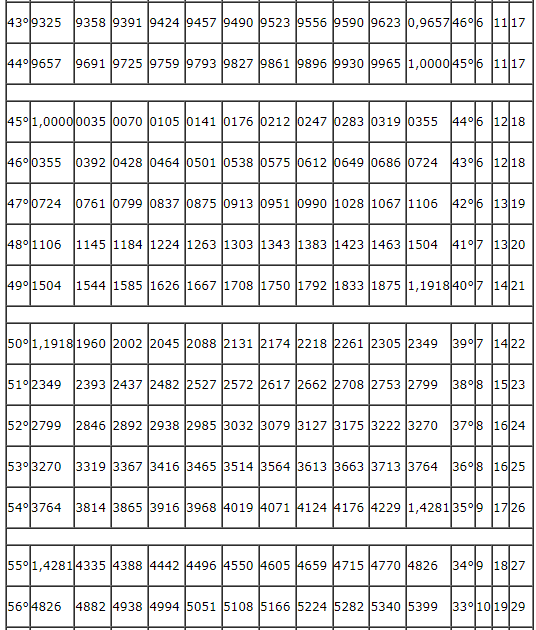
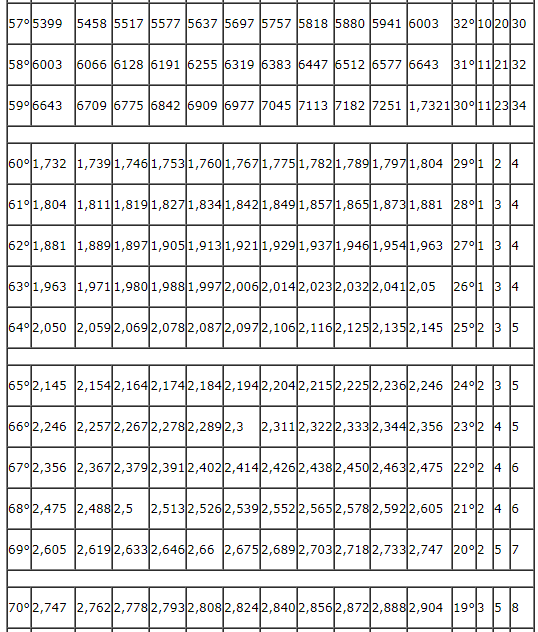
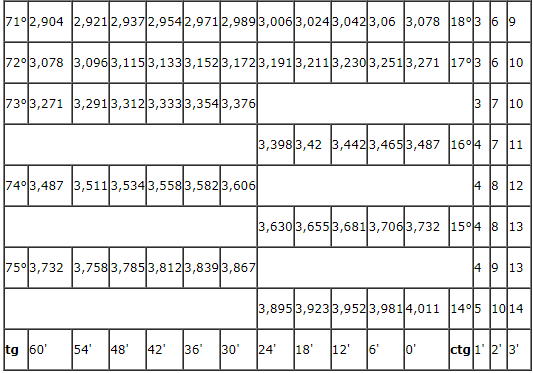
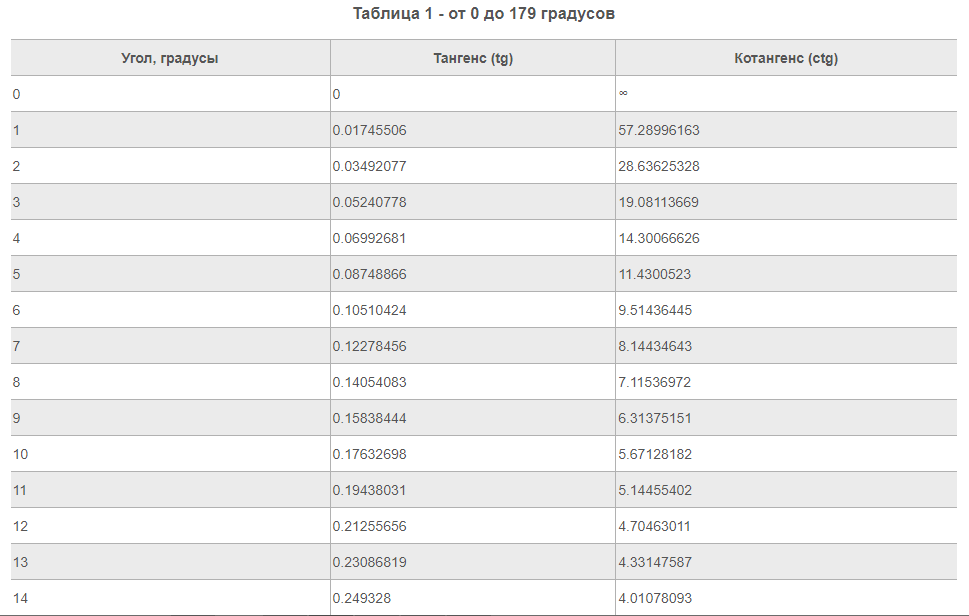
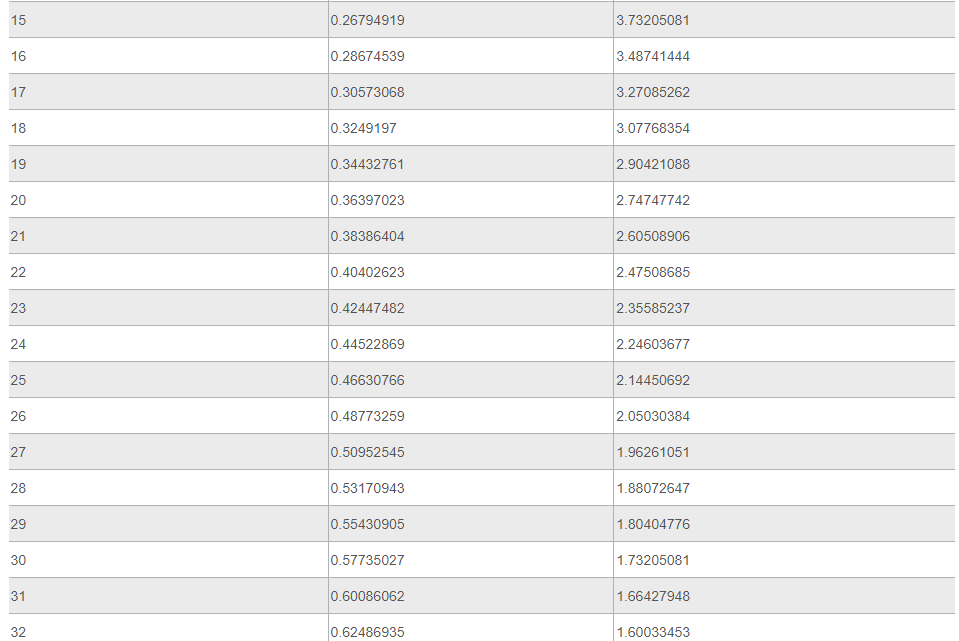
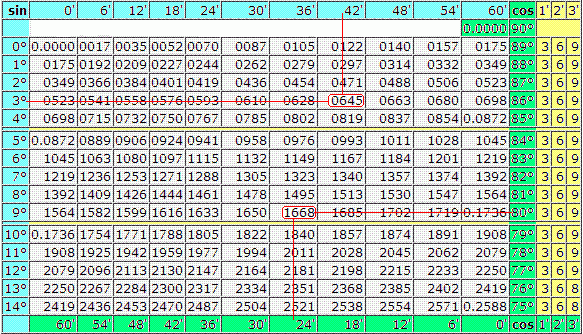
С помощью данной табличной формы можно решать задачи на тригонометрические функции. Основная таблица содержит пару разделов. В первом блоке числовой таблицы Брадиса находятся значения, которым соответствует тангенс углов от 0 до 75 градусов, а также котангенс углов от 15 до 90 градусов, определяемые по специальным столбцам для нескольких минут. Второй раздел посвящен тангенсам углов от 75 до 90 градусов и котангенсам углов от 0 до 15 градусов. Данные значения указаны точно до минуты.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: www.calc.ru
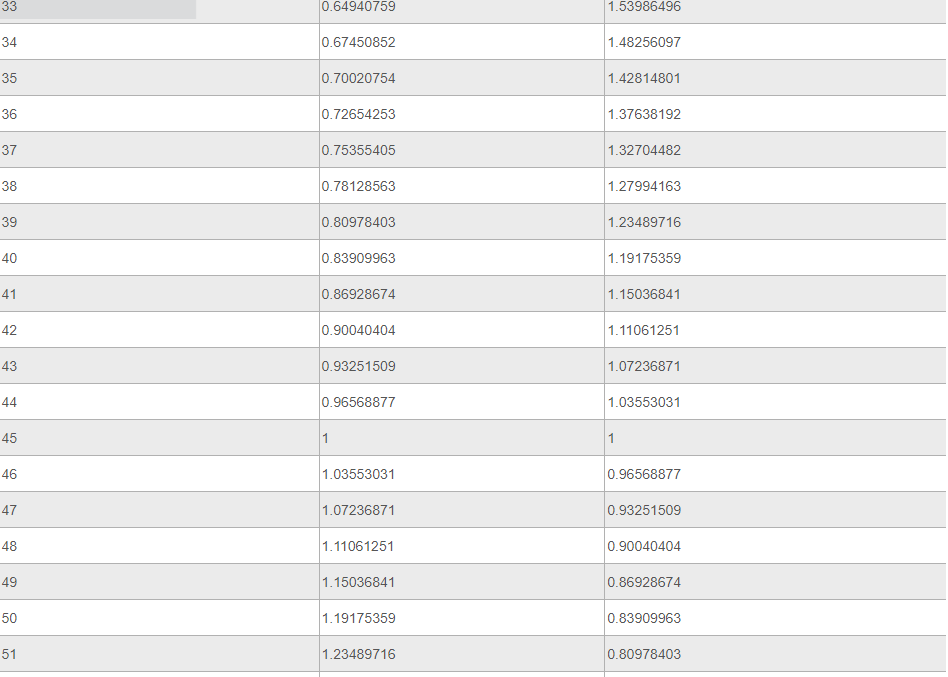
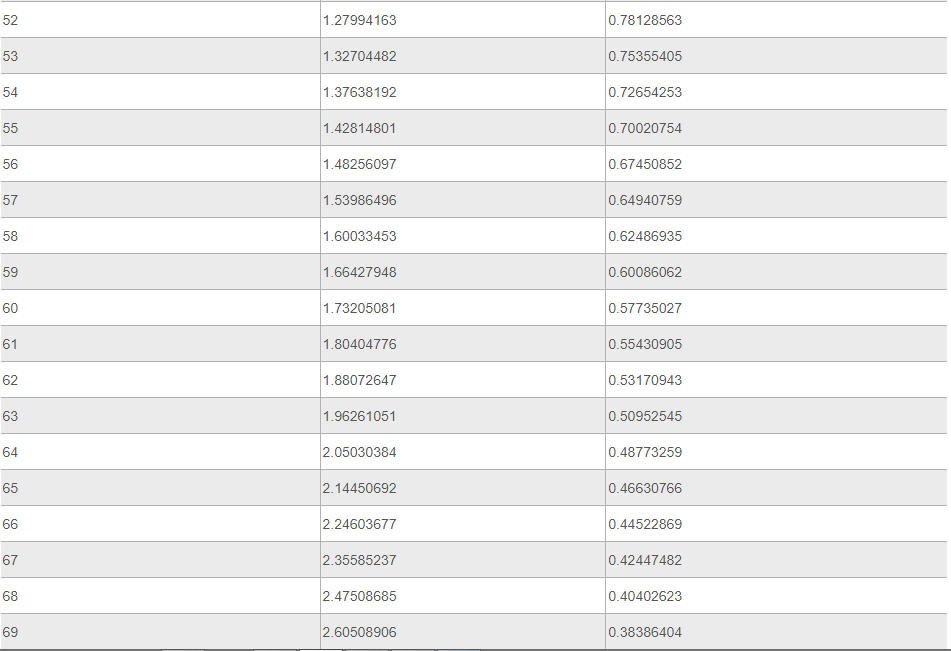
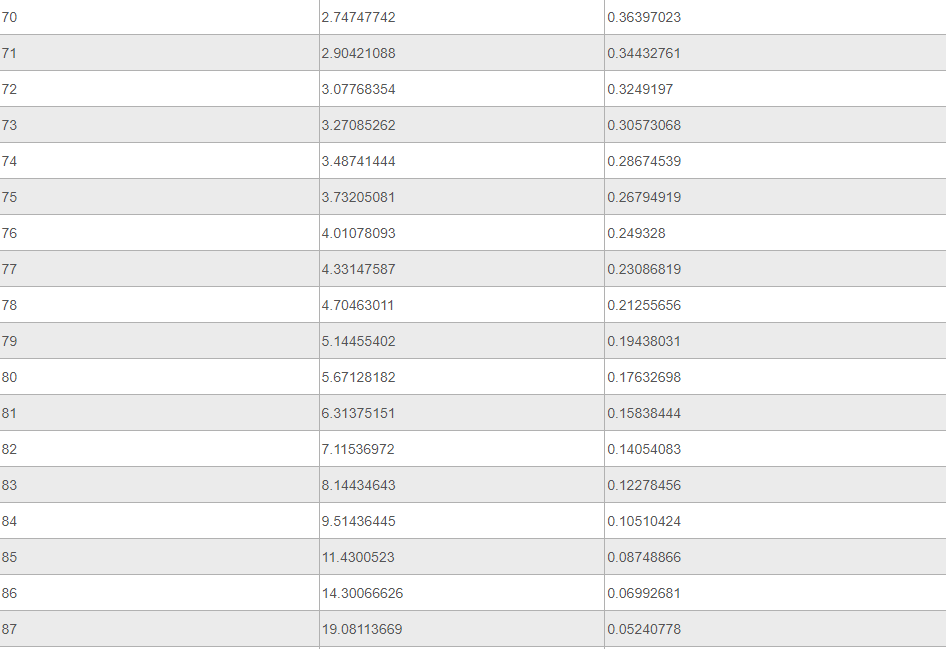
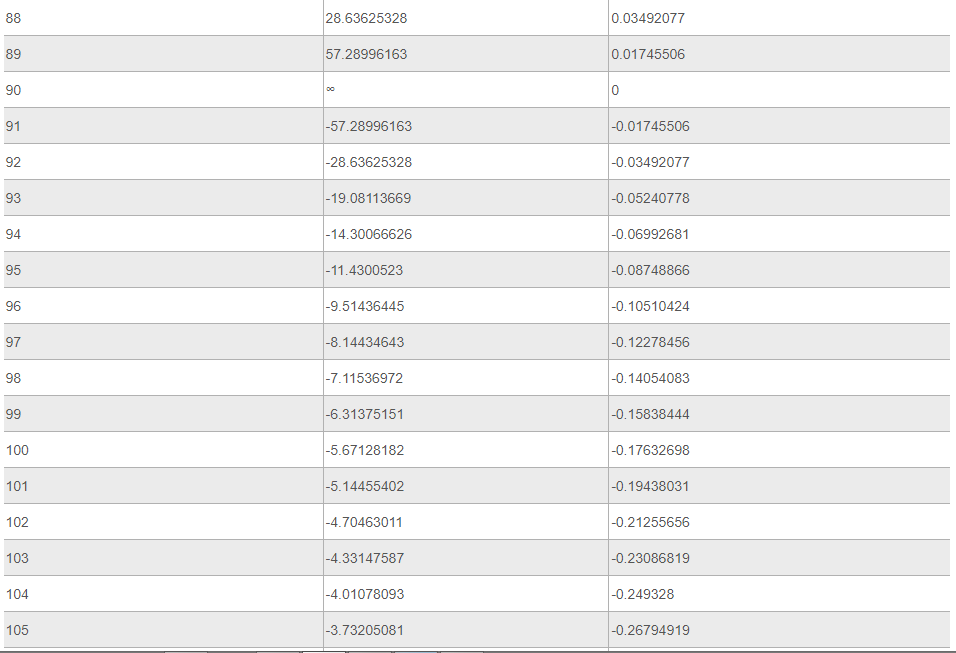
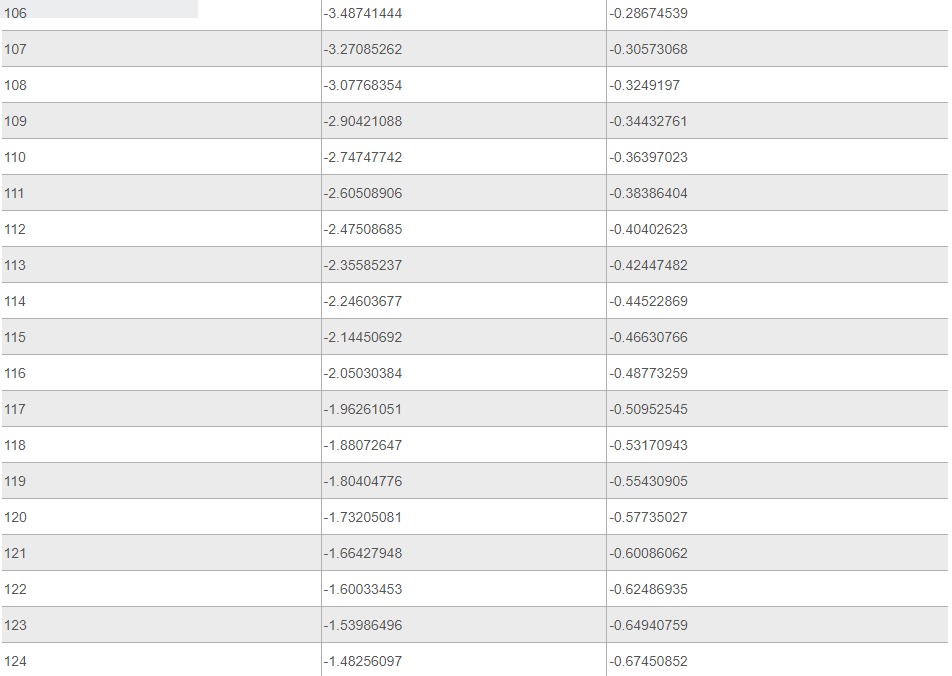
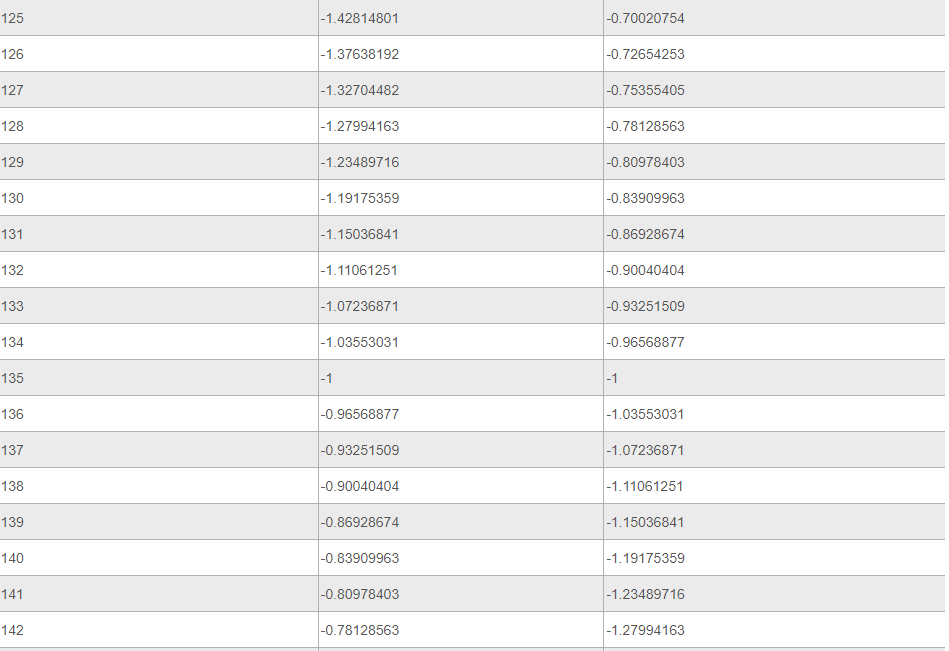
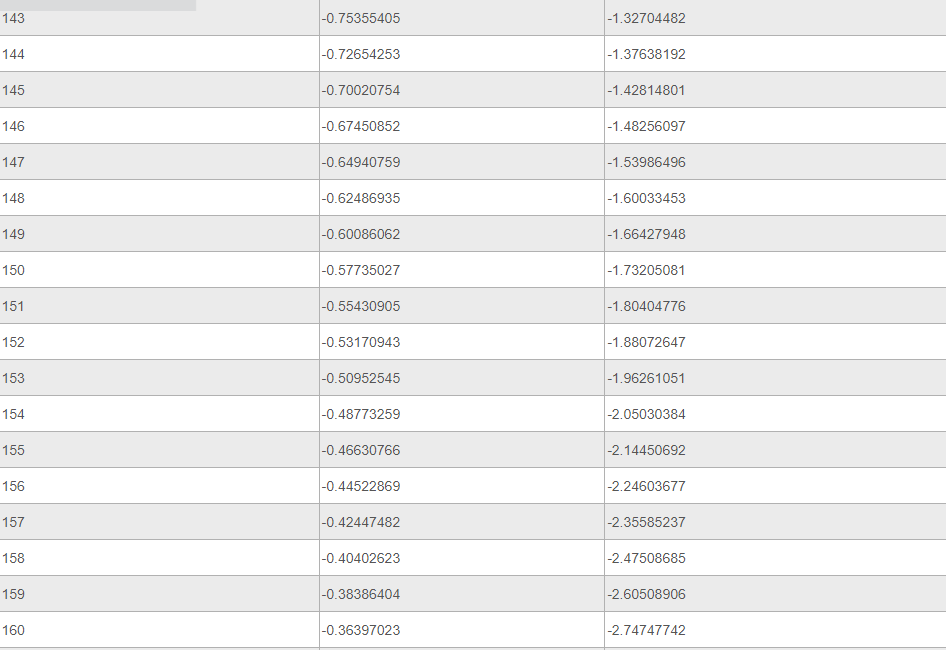
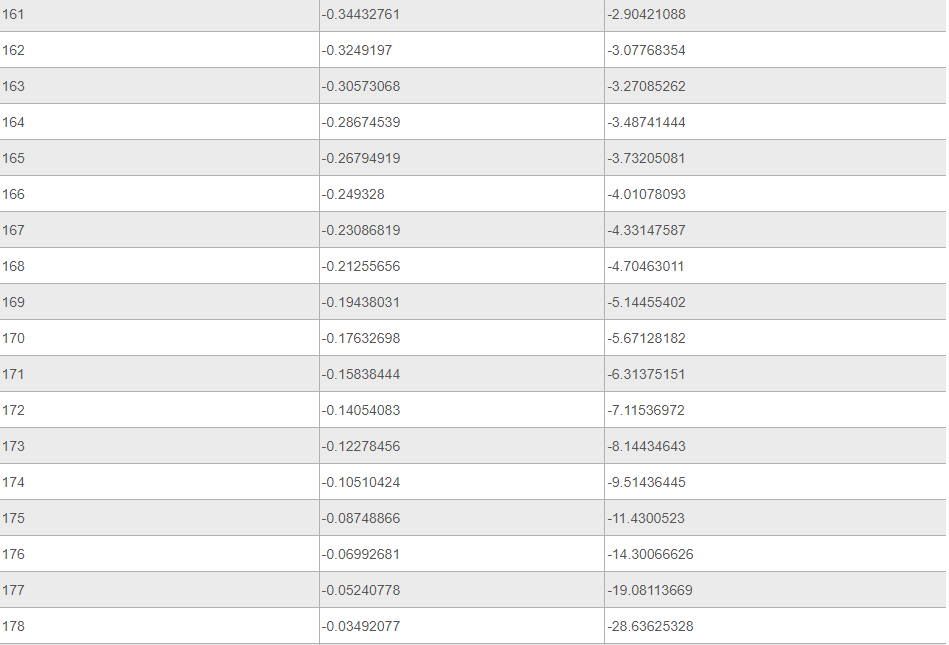
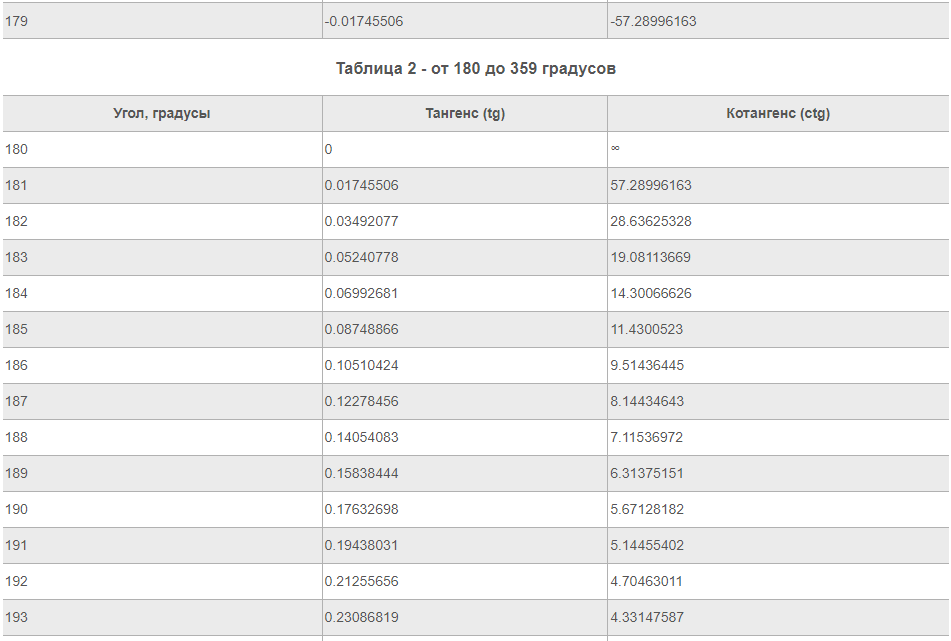
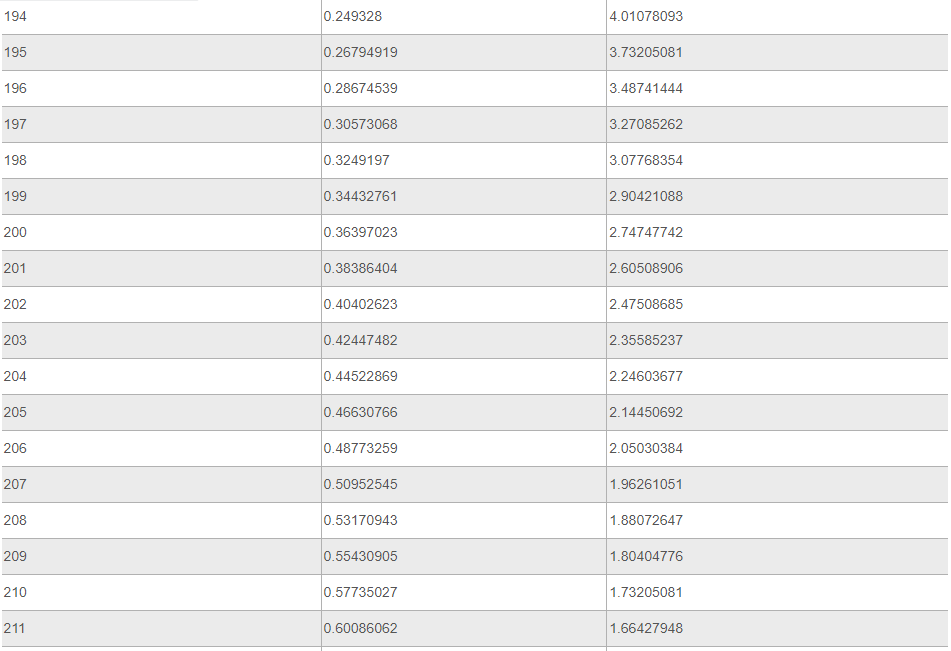
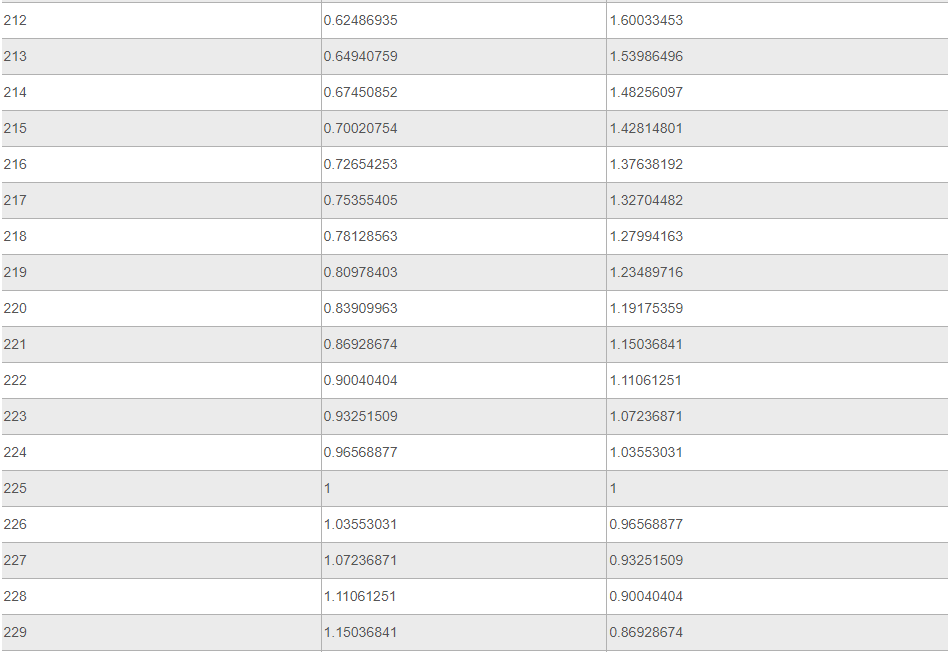
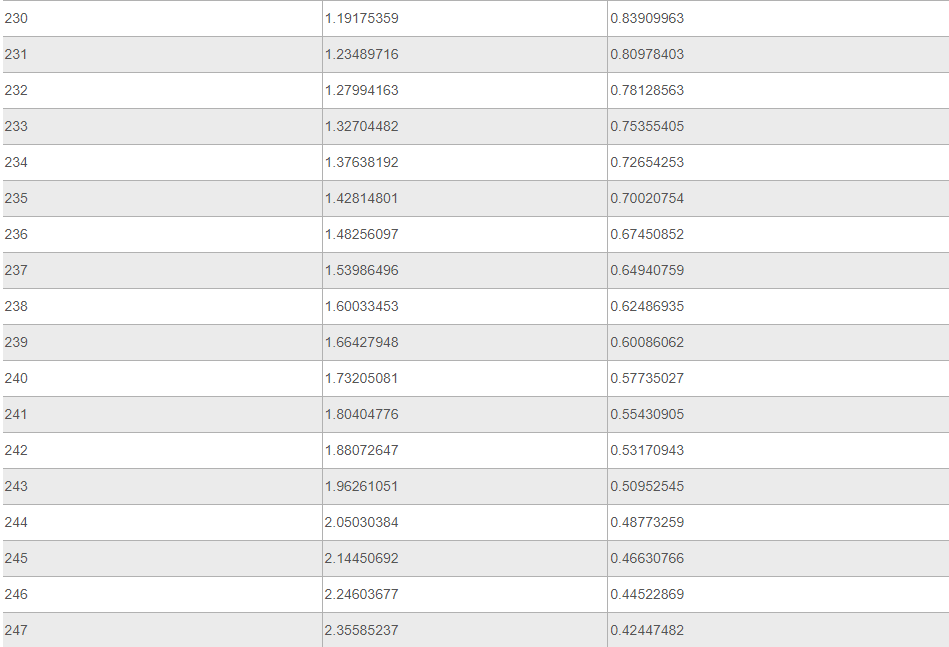
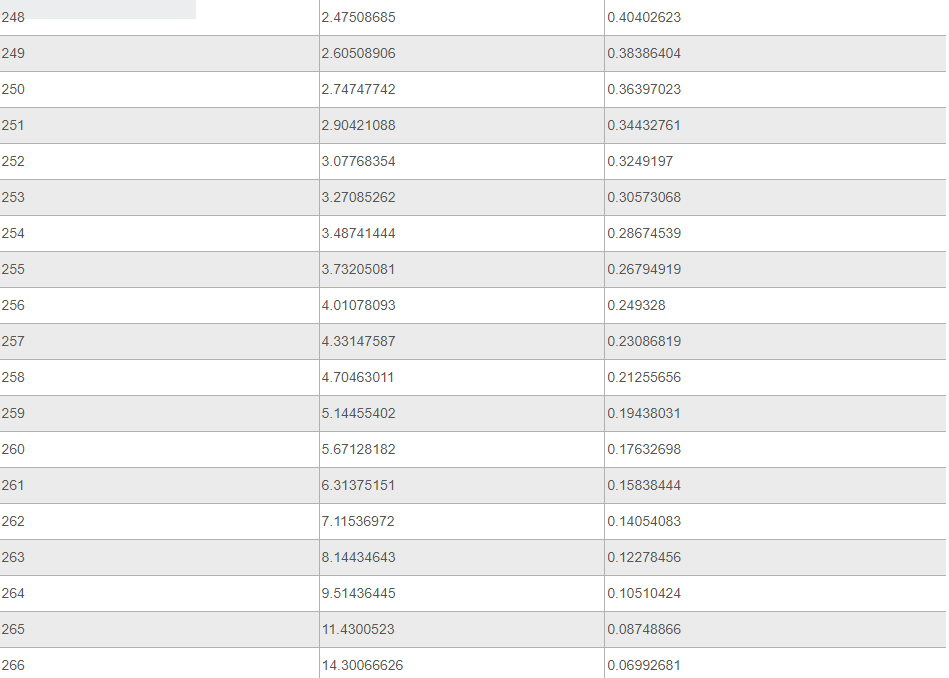
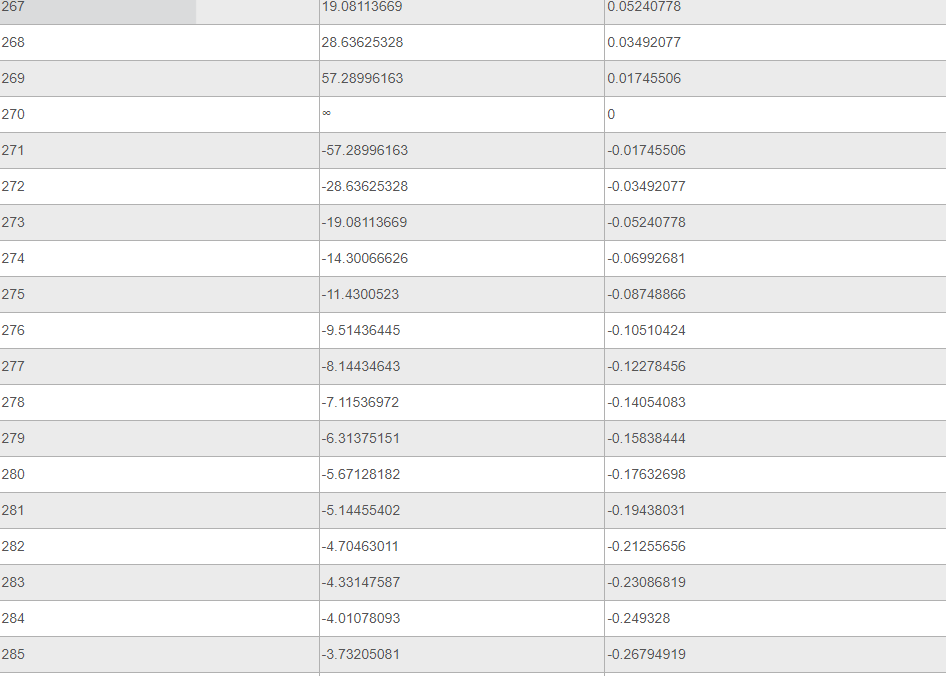
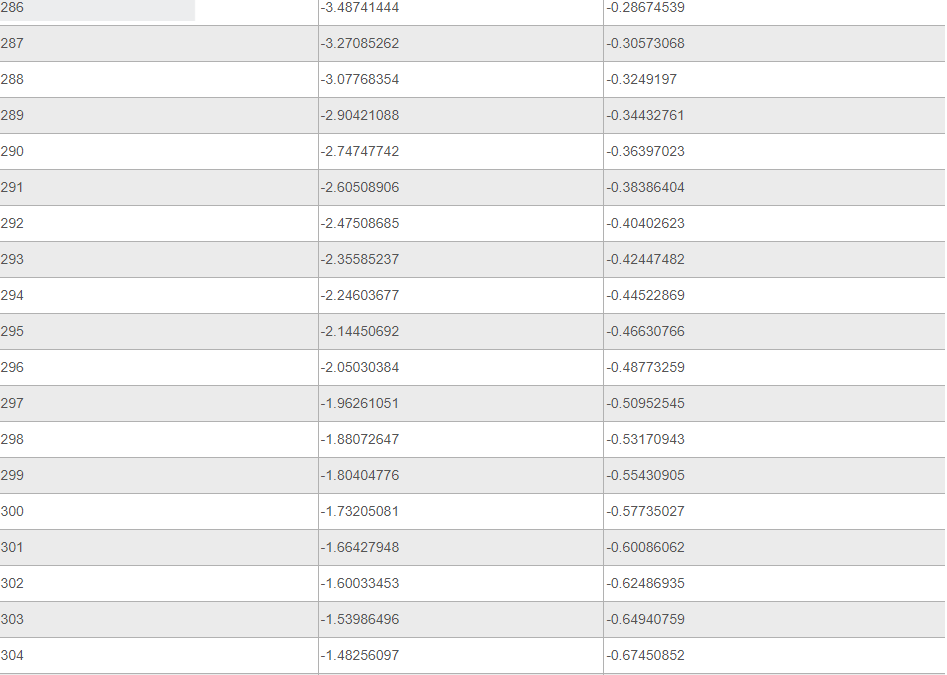
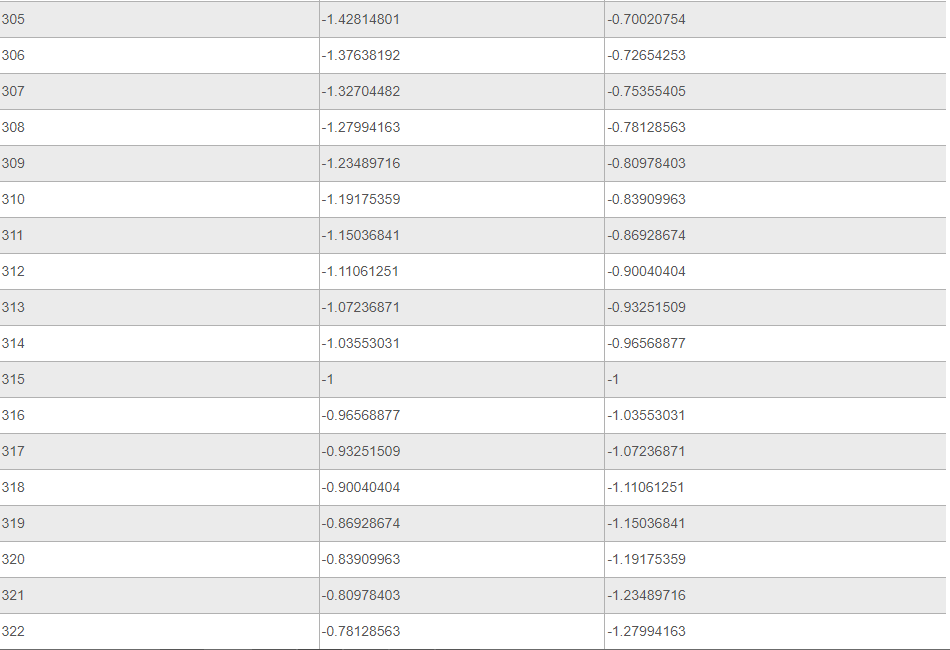
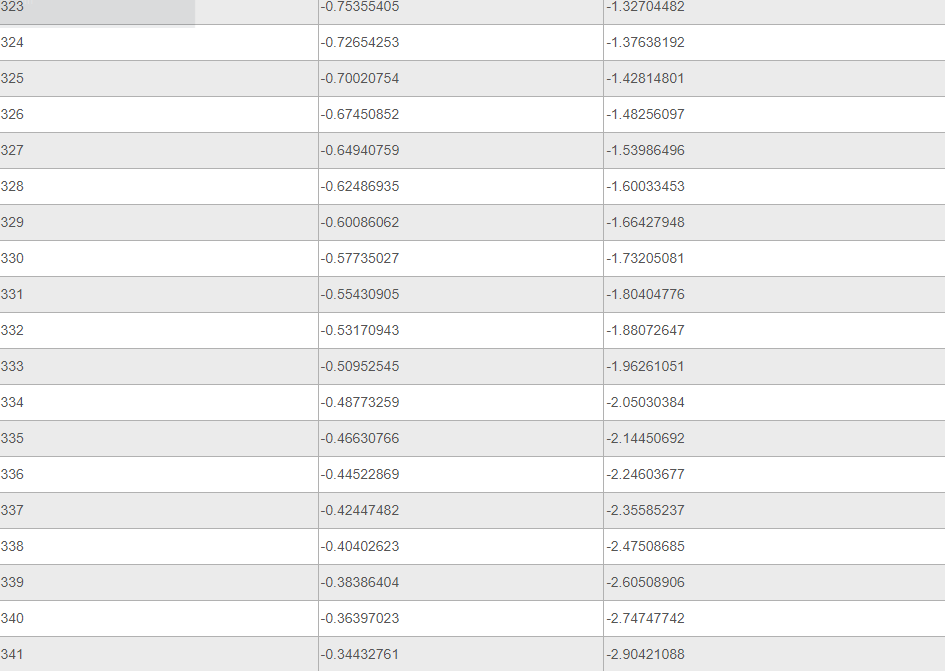
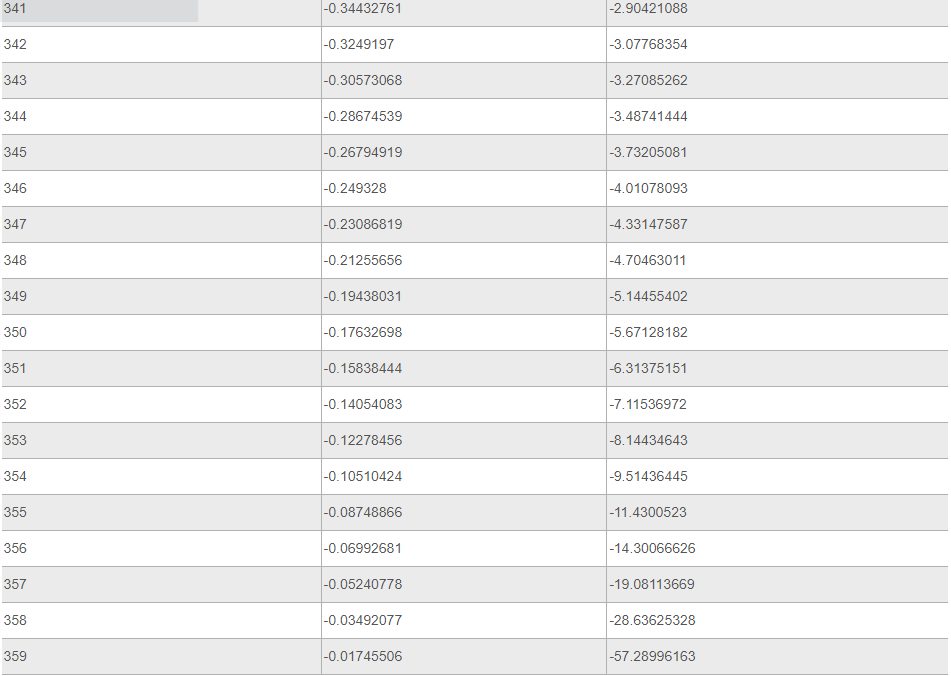
Ниже представлена таблица, где указаны значения таких тригонометрических функций, как тангенс и котангенс. Величины обозначены для углов от 0 до 360 градусов.
Источник: your-online.ru
На уроках тригонометрии можно встретить задачи, когда необходимо вычислить тангенс или котангенс углов, которые не указаны в таблице. При отсутствии табличного значения функции, к примеру, если в записи присутствуют минуты и секунды или знак минуса, то целесообразно выполнить расчет в специальном калькуляторе.
Для чего нужна
Трудно представить современный мир без достижений инженерии. Сегодня специалисты используют разнообразные программы и электронные сервисы для проведения громоздких вычислений в процессе подготовки сложных проектов. Ранее подобные задачи можно было решить лишь с помощью подручных инструментов, к примеру, рассчитать значения тригонометрических функций, применяя таблицу Брадиса.
Благодаря изобретению русского математика Владимира Модестовича Брадиса значительно уменьшились расчеты, с необходимостью выполнения которых сталкивались инженеры того времени. Для того чтобы найти искомую величину, не требовался калькулятор. Табличная форма содержала в себе наиболее часто используемые функциональные величины. В ячейках были представлены значения их аргументов с максимально возможной точностью. Таблица была опубликована в формате справочной брошюры. Печатное пособие завоевало большую популярность и издавалось практически каждый год.
Следует отметить, что таблицы Брадиса имеют однотипную структуру. Слева и вверху записаны значения, характерные для аргумента. Величина той или иной функции представлена в ячейке, совпадающей с участком, на котором пересекаются строки и столбцы. Зная о взаимосвязи тригонометрических функций, в том числе, синуса и косинуса, тангенса и котангенса, с помощью табличной формы с синусами достаточно просто вычислить значения для косинуса. При наличии таблицы с тангенсами легко определить, чему соответствует котангенсы. Заметим, что аргументы для косинуса и котангенса представлены справа и снизу в табличной форме.
Значения аргументов в таблице Брадиса выражены градусной мерой углов. При решении некоторых примеров может пригодиться навык перевода градусов в радианы. Например, чтобы узнать радианную меру угла, нужно помножить градусы на 180 и поделить на 3,1415926. При необходимости целесообразно воспользоваться специальной табличной формой, где предусмотрены значения аргумента в радианах.
Как пользоваться таблицей Брадиса
Таблица Брадиса представляет собой табличную форму, предназначенную для выполнения расчетов значений тригонометрических функций.
Таблицей Брадиса пользуются школьники на уроках алгебры. Данный материал пригодится студентам, которые получают средне-специальное и высшее образование на факультетах инженерии, архитектуры, математики, физики и других профильных дисциплин.
Применение таблицы Брадиса на практике не вызывает трудностей. Рассмотрим наглядный пример определения значений тригонометрических функций.
Источник: www.calc.ru
Источник: www.calc.ru
Аналогичным образом с помощью рассматриваемой таблицы вычисляют значения для тангенса и котангенса.
Источник: www.calc.ru
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так