Какими свойствами обладает равнобедренный треугольник — основные сведения
Равнобедренный треугольник — это… Что такое Равнобедренный треугольник?
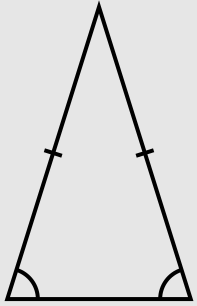
Равнобедренным называют такой треугольник, который имеет две равные по длине стороны из трех.
Стороны, которые равны, являются боковыми сторонами в равнобедренном треугольнике. Третья сторона играет роль его основания. Согласно доказательству по определению, любой правильный треугольник можно назвать равнобедренным. Обратное утверждение не является верным. Угол, расположенный между боковыми сторонами считают вершинным углом. Остальные углы являются углами при основании равнобедренного треугольника.
Признаки, составляющие элементы и свойства равнобедренного треугольника
Перечислим основные свойства, которые допустимо сформулировать для равнобедренного треугольника:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
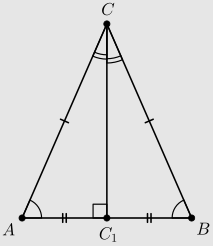
- В равнобедренном треугольнике можно провести одну ось симметрии, проходящую через вершинный угол и середину основания. Данный отрезок аналогичен биссектрисе вершинного угла, медиане, которая проведена к основанию, высоте, построенной из вершинного угла, серединному перпендикуляру.
- Углы, расположенные напротив равных сторон, обладают одинаковой градусной мерой в равнобедренном треугольнике. Кроме того, для такой фигуры характерно равенство биссектрис, медиан и высот, которые построены из равных углов.
- В равнобедренном треугольнике совпадают биссектриса, медиана, высота и серединный перпендикуляр. На этих отрезках расположены центры окружностей, описанных и вписанных в равнобедренный треугольник.
Рассмотрим соотношения составляющих элементов в равнобедренном треугольнике. Обозначим а за длину двух соответствующих друг другу сторон, b является длиной основания, h обозначает высоту.
Из теоремы косинусов вытекает такое соотношение:
\(a={\frac b{2\cos \alpha }}\)
С помощью теоремы синусов можно записать следующее равенство:
\(b=a{\sqrt {2(1-\cos \beta )}}\)
\(b=2a\sin {\frac \beta 2}\)
Согласно теореме о проекциях:
\(b=2a\cos \alpha\)
При известных двух параметрах равнобедренного треугольника радиус окружности, которая в него вписана, можно рассчитать одним из предложенных вариантов:
\(r={\frac b2}{\sqrt {{\frac {2a-b}{2a+b}}}}\)
\(r={\frac {bh}{b+{\sqrt {4h^{2}+b^{2}}}}}\)
\(r={\frac {h}{1+{\frac {a}{{\sqrt {a^{2}-h^{2}}}}}}}\)
\(r={\frac b2}\operatorname {tg}\left({\frac {\alpha }{2}}\right)\)
\(r=a\cdot \cos(\alpha )\cdot \operatorname {tg}\left({\frac {\alpha }{2}}\right)\)
Углы в равнобедренном треугольнике находят таким образом:
\(\alpha ={\frac {\pi -\beta }2}\)
\(\beta =\pi -2\alpha\)
\(\alpha =\arcsin {\frac a{2R}},\beta =\arcsin {\frac b{2R}}\)
При расчете углов допустимо исключить \({\pi }\) и \(R\). Тогда следует поделить треугольник с помощью медианы на две части и вычислить углы по формуле:
\(y=\cos \alpha ={\frac {b}{c}},\arccos y=x\)
Соотношения, выражающие периметр равнобедренного треугольника:
\(P=2a+b\)
\(P=2R(2\sin \alpha +\sin \beta )\)
Определить, чему равна площадь равнобедренного треугольника можно разными способами, к примеру:
\(S={\frac {1}{2}}bh\)
\(S={\frac 12}a^{2}\sin \beta ={\frac 12}ab\sin \alpha ={\frac {b^{2}}{4\tan {\frac \beta 2}}}\)
\(S={\frac {1}{2}}b{\sqrt {\left(a+{\frac {1}{2}}b\right)\left(a-{\frac {1}{2}}b\right)}}\)
Перечислим характерные признаки равнобедренного треугольника:
- При наличии в произвольном треугольнике пары равных друг другу углов, справедливо заметить, что такой треугольник является равнобедренным, а равные углы расположены при его основании.
- В случае совпадения высоты и медианы, либо высоты и биссектрисы, либо биссектрисы и медианы в каком-то треугольнике можно считать такой треугольник равнобедренным. При этом сторона, к которой построены перечисленные элементы фигуры, играет роль основания.
Как пользоваться свойствами и признаками равнобедренного треугольника при решении задач
Представим, что имеется некий равнобедренный треугольник АВС. Пусть его боковая сторона в 4 раза больше по сравнению с основанием, а периметр составляет 27. Требуется определить, чему равна длина боковой стороны этого треугольника.
Введем следующее обозначение:
\(AC=x\)
В таком случае:
\(AB=BC=4x.\)
Вычислим периметр треугольника:
\({{P}_{ABC}}=AB+BC+AC=4x+4x+x=9x=27\)
В результате:
\(х=3\)
\(AB=BC=4\cdot 3=12\)
Ответ: \(AB=BC=12 см\)
Равнобедренный треугольник \(АВС\) имеет основание \(АС\). Построим в нем медиану \(м\). Требуется найти угол А при условии, что \(\angle KBC={{50}^{\circ}}.\)
Заметим, что в равнобедренном треугольнике медиана, которая построена к его основанию, играет роль биссектрисы и высоты. Таким образом:
\(\angle ABK=\angle KBC={{50}^{\circ}}, \quad \angle AKB={{90}^{\circ}}\)
При рассмотрении прямоугольного треугольника \(АВК\) можно записать следующее равенство:
\(\angle A={{180}^{\circ}}-{{90}^{\circ}}-{{50}^{\circ}}={{40}^{\circ}}\)
Ответ: \(\angle A={{40}^{\circ}}\)
Задачи для самостоятельного решения
Треугольник \(АВС\) характеризуется следующими параметрами:
\(\angle C = 40^{\circ}\)
\(\angle B = 110^{\circ}\)
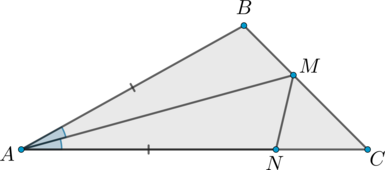
Требуется вычислить градусную меру \(\angle CMN\), если \(AM\) является биссектрисой, \(N\) обозначает точку на \(АС\), а \(AB = AN.\)
Решение
\(\angle BAC = 180^{\circ} - \angle B - \angle C = 180^{\circ} - 110^{\circ} - 40^{\circ} = 30^{\circ}\)
\(\angle MAN =\cdot \angle BAM = 15^{\circ}\)
\(\angle BMA = \angle AMN\)
\(\angle BMA = 180^{\circ} - \angle BAM - \angle B = 180^{\circ} - 15^{\circ} - 110^{\circ} = 55^{\circ}\)
\(\angle BMN = 2\cdot \angle BMA = 110^{\circ}\)
\(\angle CMN = 180^{\circ} - 110^{\circ} = 70^{\circ}\)
Ответ: 70.
Треугольник \(АВС\) характеризуется следующими параметрами:
\(\angle A = 51^{\circ}\)
\(\angle C = 77^{\circ}\)
При этом \(BD\) является биссектрисой, а точка \(Р\) делит отрезок \(АВ\) на равные отрезки \(PB\) и \(BC\). Нужно определить градусную меру \(\angle ADP\).
Решение
\(\angle ABC = 180^{\circ} - \angle A - \angle C = 180^{\circ} - 51^{\circ} - 77^{\circ} = 52^{\circ}\)
\(\angle CBD = 0,5\cdot \angle ABC = 26^{\circ}\)
\(\angle PDB = \angle CDB\)
\(\angle CDB = 180^{\circ} - \angle CBD - \angle C = 180^{\circ} - 26^{\circ} - 77^{\circ} = 77^{\circ}\)
\(\angle PDC = 2\cdot \angle CDB = 154^{\circ}\)
\(\angle ADP = 180^{\circ} - 154^{\circ} = 26^{\circ}\)
Ответ: 26.
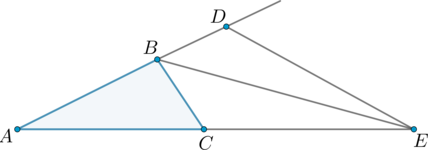
Треугольник \(АВС\) образован углами \(\angle A = 22^{\circ}\) и \(\angle C = 40^{\circ}\). При этом \(BE\) играет роль биссектрисы внешнего угла при вершине B. На продолжении стороны АС отмечена точка Е. На продолжении стороны AB за точку B выбрана точка D, так, что \(BC = BD\). Требуется найти \(\angle CED\).
Решение
\(\angle CBD = \angle A + \angle ACB = 22^{\circ} + 40^{\circ} = 62^{\circ}\)
\(\angle CBE = 0,5 \cdot \angle CBD = 31^{\circ}\)
\(\angle BCE = 180^{\circ} - \angle ACB = 140^{\circ}\)
\(\angle BEC = 180^{\circ} - \angle CBE - \angle BCE = 9^{\circ}\)
\(\angle CED = 2\cdot \angle BEC = 18^{\circ}\)
Ответ: 18.
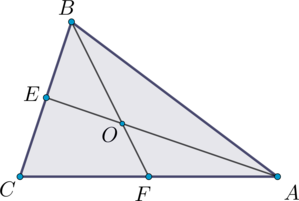
Треугольник \(АВС\), в котором проведены медианы \(BF\) и \(AE\), характеризуется следующими элементами:
\(AE = BF\)
\(\angle FOE = 147^{\circ}\)
При этом \(BF\) и \(AE\) пересекаются в точке О. Нужно определить \(\angle ABO\).
Решение
\(\angle AOB = \angle FOE = 147^{\circ}\)
\(AO = \dfrac{2}{3}AE = \dfrac{2}{3}BF = BO\)
\(\angle OAB = \angle ABO\)
\(180^{\circ} = \angle OAB + \angle ABO + \angle AOB = 2\cdot \angle ABO + 147^{\circ}\)
\(\angle ABO = 16,5^{\circ}\)
Ответ: 16,5.
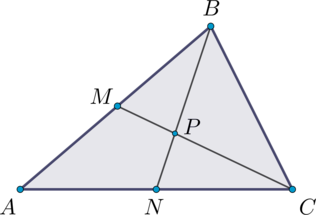
В треугольнике \(АВС\) проведены медианы \(BN\) и \(CM\). На пересечении \(BN\) и \(CM\) отмечена точка Р. При этом \(\angle PBC = 35^{\circ}\), \(\angle BPC = 110^{\circ}\), \(AB = 4\). Требуется определить длину \(NC\).
Решение
\(\angle PCB = 180^{\circ} - 110^{\circ} - 35^{\circ} = 35^{\circ} = \angle PBC\)
\(PB = PC\)
\(MP = 0,5\cdot PC = 0,5 \cdot PB = PN\)
\(\angle MPB = \angle NPC\)
\(NC = MB = 0,5\cdot AB = 2\)
Ответ: 2.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так