Понятие и свойства логарифма, формулы

Что такое логарифм

Обозначают логарифм следующим образом:

\(\log _{a}b\)

При решении математических задач, в том числе с модулем, требуется не только представить корректный ответ, но и объяснить преподавателю ход решения. В этом случае необходимо правильно сформулировать рассматриваемые величины. Имея дело с логарифмическими выражениями, следует руководствоваться такой формулировкой: «логарифм b по основанию a».

Обратимся еще раз к записанному выше определению. Заметим, что при необходимости вычисления такого уравнения:

\(x=\log _{a}b\)

Можно считать данное выражение равным по смыслу следующей записи:

\(a^{x}=b\)

Это утверждение легко проверить на практике. Рассмотрим типичный пример.

В процессе рассмотрения темы логарифмов целесообразно упомянуть об их особых свойствах. Благодаря ряду уникальных характеристик, логарифмы получили широкое распространение в разных научных областях, в том числе, алгебре, физике, геометрии. С помощью разнообразных упрощений можно решать быстро и легко трудоемкие примеры и задачи.

Применяя свойства логарифмирования, достаточно просто трансформировать умножение в операцию сложения, а деление заменить компактным вычитанием. Логарифмы позволяют выполнить замену выражений, где предполагается возведение в степень, на умножение. Кроме того, аналогичным образом извлечение корней записывают в форме деления. По мнению знаменитого ученого Лапласа, открытие логарифмов упростило труд астронома и удвоило его жизнь.

По мере накопления знаний о логарифмах было установлено, что функцию в виде \(y=\log _{a}x\) допустимо использовать в разных сферах научной деятельности. С ее помощью, к примеру, решают следующие задачи:

• поиск корней дифференциальных уравнений;
• классификация значений величин, в том числе, частоты и интенсивности звуковых волн;
• аппроксимация различных зависимостей;
• теория информации;
• теория вероятностей.

Логарифмическая функция является элементарной и обратной к показательной функции. В распространенных случаях при решении классических и нетривиальных задач можно встретить вещественные логарифмы, основания которых равны:

• 2 (двоичный);
• число Эйлера e (натуральный);
• 10 (десятичный логарифм).

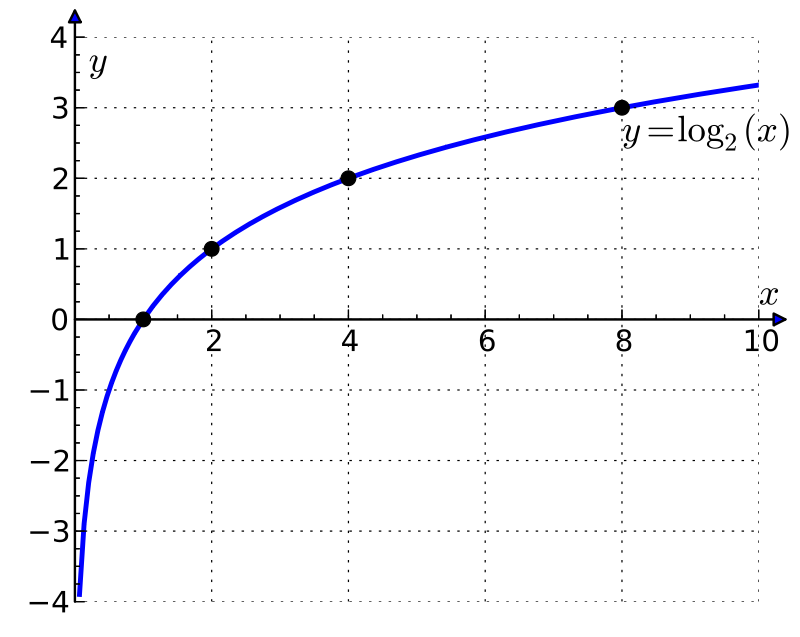
В качестве наглядного примера изобразим графически двоичный логарифм:

 

Источник: ru.wikipedia.org

Исходя из данного ранее определения, логарифм вещественного числа \(x=\log _{a}b\) представляет собой решение следующего уравнения:

\(a^{x}=b\)a

Представим, что а равно единице. Если  \(b\neq 1\) при заданных условиях, то у записанного уравнения отсутствуют корни. Предположим, что b также равно единице, как и а. Тогда можно заключить, что какое-либо число подходит на роль решения рассматриваемого уравнения. Сделаем вывод, что в обеих описанных ситуациях логарифм не определен.

В том случае, когда а имеет значение, равное нулю или со знаком минус, существование логарифма невозможно. Исходя из того, что значение, которому соответствует показательная функция \(a^{x}\) в любом варианте будет со знаком плюс,  необходимо исключить вероятность принятия b отрицательного значения. Подведем итог и запишем его в математической форме: вещественный логарифм \(\log _{a}b\) обладает смыслом, если  \(a>0,a\neq 1,b>0\).

Если записанные условия для а выполнимы, то показательная функция \(y=a^{x}\) существует, является монотонной и принимает определенное значение единожды, а это значение соответствует множеству всех положительных вещественных чисел. Таким образом, можно сделать вывод о существовании значения вещественного логарифма положительного числа, которое определено однозначно.

Основные свойства логарифмов

С логарифмами можно производить разные математические операции. Подобно и любым другим числам, логарифмы складывают, вычитают, а также выполняют преобразование данных выражений. С другой стороны, логарифмы сложно назвать простыми числами. По этой причине любые манипуляции с ними регламентированы специальными правилами, которые называют основными свойствами логарифмов.

Рассматриваемые правила можно найти в любом учебнике и пособии. Однако запомнить их не составит труда. В таком случае получится существенно упростить вычисления задач и примеров. Свойства логарифмов предназначены для упрощения решения достаточно сложных и трудоемких расчетов. Стоит отметить, что их не так много. Важно понять, смысл этих свойств, чтобы научиться правильно их применять.

Вынесение показателя степени из логарифма

На практике нередко встречаются примеры, когда основание или аргумент логарифма содержат в записи степень. При необходимости допустимо избавиться от степенного показателя путем его вынесения за знак логарифма. В процессе следует соблюдать такие правила, как:

\(\log _{a}(x^{n})=n \cdot \log _{a}(x)\)

\(\log _{(a^{k})}(x)={\frac {1}{k}}\log _{a}(x)={\frac {\log _{a}(x)}{k}}\)

\(\log _{(a^{k})}(x^{n})={\frac {n}{k}}\log _{a}(x)\)

Представим доказательства первого выражения:

\(\log _{a}(x^{n})=n \cdot \log _{a}(x)\)

\(\log _{a}{x^{ n }}=y\)

\(a^{y}=x^{ n }\)

\(a^{\frac {y}{n}}=x\)

\(log_{a}{x}={\frac {y}{ n}}\)

\(n\cdot log_{a}{x}=y\)

Докажем, что следующее записанное выражение является справедливым равенством:

\(\log _{(a^{k})}(x)={\frac {1}{k}}\log _{a}(x)={\frac {\log _{a}(x)}{k}}\)

\(\log _{a^{p}}{x}=y\)

\(a^{y\cdot p}=x\)

\(log_{a}{x}=p\cdot y\)

\({\frac {log_{a}{x}}{p}}=y\)

Если представится возможность применить записанные свойства на практике, то необходимо помнить об ОДЗ. В случае логарифма таковыми условиями являются:

\(a > 0, a \neq 1, x > 0\)

Заметим, что корректность записанных свойств не меняется, если применять их в любую сторону. Числа, которые расположены перед логарифмическим знаком, допустимо записывать непосредственно в логарифм.

Решение

Используя уже знакомое свойство логарифма, исключим из аргумента степень:

\(\log _{7}(49^{6}) = 6 \cdot \log _{7}(49) = 6 \cdot 2 = 12\)

Ответ: 12.

Решение

Обратим внимание на знаменатель, записанный в виде логарифма с основанием и аргументом, которые равны точным степеням, то есть:

\(16 = 2^{4}\)

\(49 = 7^{2}\)

Получим следующее выражение, которое можно преобразовать:

\(\frac{\log _{2}(7)}{\log _{16}(49)} = \frac{\log _{2}(7)}{\log _{2^{4}}(7^{2})} = \frac{\log _{2}(7)}{ \frac{2}{4}\cdot \log _{2}(7)} = \frac{4}{2} = 2\)

Ответ: 2.

Сложение и вычитание логарифмов

Далее перейдем к операциям сложения и вычитания логарифмов. На этот случай также есть уникальное свойство, с помощью которого допустимо упрощать многие сложные расчеты.

\(\log _{a}(x)+\log _{a}(y) = \log _{a}(xy)\)

\(\log _{a}(x)-\log _{a}(y) = \log _{a}\!\left({\frac {x}{y}}\right)\)

Здесь важно помнить о равенстве оснований логарифмов, которые участвуют в расчетах. Приведем практический пример.

Решение

Руководствуясь свойством сложения логарифмов, выполним соответствующие преобразования:

\(\log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5\)

Ответ: 5

Решение

Воспользуемся свойством вычитания логарифмов и преобразуем выражение, чтобы получить ответ:

\(\lg \left({\frac {1}{1000}}\right)=\lg(1)-\lg(1000)=0-3=-3\)

Ответ: -3

Основное логарифмическое тождество

Не во всех задачах требуется выполнить сложение или вычитание логарифмов. Встречаются и такие примеры, в которых необходимо записать число в виде логарифма по определенному в условии основанию. Тогда пригодится главное логарифмическое тождество.

Вновь обратимся к понятию логарифма. Исходя из определения, можно сделать следующий вывод:

\(a^{\log _{a}b}=b\)

Таким образом, при равенстве пары вещественных логарифмов справедливым является равенство логарифмируемых выражений. Запишем это утверждение в математической форме:

\(\log _{a}b=\log _{a}c\)

Тогда получим:

\(a^{\log _{a}b}=a^{\log _{a}c}\)

В результате:

b=c.

Решение

Заметим, что в данном случае можно вынести квадрат из основания и аргумента. В итоге получим:

\(\log _{25}64 = \log _{5}8\)

Воспользуемся основным логарифмическим тождеством и решим пример:

\(5^{2+\log _{5}8} = 5^{2}\cdot 5^{\log _{5}8} = 25 \cdot 8 = 200\)

Ответ: 200.

Переход к новому основанию

Ранее рассмотренные правила, регламентирующие то, как корректно складывать и вычитать логарифмы, справедливы лишь в том случае, когда они имеют идентичные основания. Однако не во всех задачах выражения приведены к нужному виду.  В большинстве случаев придется выполнить несколько простых манипуляций, чтобы перейти к новому основанию.

Вывести свойство, упрощающее переход к новому основанию логарифма, можно путем доказательства теоремы. Представим, что имеется некий логарифм:

\(\log _{а}х\)

В таком случае, для каждого из чисел с при условии, что \(с > 0\) и  \(с \neq 1\), справедливым является следующее равенство:

\(\log _{а}х = \frac{\log _{с}х }{\log _{с}а}\)

Если с = х, то записанное выражение можно преобразовать таким образом:

\(\log _{а}х = \frac{1}{\log _{х}а}\)

Это равенство доказывает возможность перемены мест для основания и аргумента логарифма. В процессе преобразований необходимо перевернуть выражение. Таким образом, логарифм встает на место знаменателя.

Решение

Проанализируем записанное выражение. Аргументы каждого из логарифмов соответствуют точным степеням. Перенесем показатели таким образом:

\(\log _{5}16 = \log _{5}(2^{4}) = 4\log _{5}2\)

\(\log _{2}25 = \log _{2}(5^{2}) = 2\log _{2}5\)

Далее можно перевернуть второй логарифм:

\(4\log _{5}2\cdot 2\log _{2}5 = 8\cdot \log _{5}2 \cdot \frac{1}{\log _{5}2} = 8\)

Ответ: 8.

Решение

Заметим, что основание и аргумент логарифма являются точными степенями. Запишем это утверждение и исключим показатели:

\(\log _{9}100 = \log _{3^{2}}10^{2} = \frac{2}{2}\log _{3}10 = \log _{3}10\)

Далее целесообразно убрать десятичный логарифм путем перехода к новому основанию:

\(\log _{3}10 \cdot \lg _3 = \log _{3}10 \cdot \frac{1}{\log _{3}10} = 1\)

Ответ: 1.

Логарифмическая единица и логарифмический ноль

Существует еще пара тождеств, которые называют свойствами логарифма. Данные правила достаточно просто можно вывести из формулировки понятия:

• \(\log _{a}1=0\);
• \(\log _{a}a=1\).

Необходимость в их применении нередко встречается в задачах. С другой стороны, учащиеся часто допускают ошибки в процессе использования этих свойств.