Определение, свойства и признаки параллелограмма

Параллелограмм — это

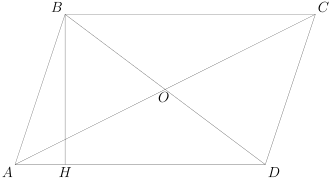
На рисунке изображен параллелограмм АВСD с точкой пересечения диагоналей О и высотой ВН:

 

Источник: ru.wikipedia.org

В практическом курсе по геометрии нередко встречаются задания на поиск разных величин параллелограмма. К данному типу фигуры причисляют также частные случаи. Приведем несколько примеров:

• ромб;
• прямоугольник;
• квадрат.

В произвольном параллелограмме можно построить диагонали. Такие линии представляют собой отрезки, соединяющие противолежащие вершины геометрической фигуры. Биссектриса, построенная из угла параллелограмма, соединяет вершину с отметкой, расположенной на какой-либо из двух противолежащих сторон, и делит на два равных сектора угол при вершине.

Площадь параллелограмма вычисляют как произведение одной стороны и высоты геометрической фигуры по формуле:

\(S = а \cdot h\)

Предусмотрено выражение для расчета площади при известной величине пары сторон и градусной меры угла между ними:

\(S = а \cdot b \cdot \sin\alpha\)

Другой способ вычисления площади параллелограмма заключается в использовании пары диагоналей и угла между ними:

\(S = 0,5 \cdot (d_{1} \cdot d_{2}) \cdot \sin \beta\)

С целью определения периметра геометрической фигуры в виде параллелограмма необходимо сложить величины сторон, которые не являются параллельными, и умножить полученный результат на два. Уравнение для расчета имеет следующий вид:

\(P = 2 \cdot (a + b).\)

Свойства

В процессе решения задач удобно применять свойства параллелограмма, которые значительно упрощают вычисления геометрических характеристик рассматриваемого типа фигуры. Перечислим основные закономерности:

1. Диагонали в параллелограмме пересекаются в отметке, которая делит каждую из них на две равные части, то есть \(\left|AO\right|=\left|OC\right|,\left|BO\right|=\left|OD\right|\), что можно проследить на изображении, представленном выше в разделе с определением фигуры.
2. С помощью какой-либо диагонали в параллелограмме выделяют пару идентичных треугольников.
3. При сложении квадратов диагональных отрезков, построенных в параллелограмме, получается величина, равная сумме квадратов пары смежных сторон рассматриваемой фигуры, умноженной на два. Предположим, что сторона АВ имеет протяженность а, сторона ВС в длину составляет b, обозначим за \(d_{1} и d_{2}\)  размеры диагональных отрезков, тогда получим следующее справедливое соотношение: \(d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2})\).
4. В параллелограмме соблюдается равенство сторон и углов, расположенных напротив друг друга.
5. Градусная мера углов, которые расположены около одной стороны, в сумме составляет 180°, что является следствием из доказательства свойства параллельности прямых.
6. Точку, в которой пересекаются диагональные прямые, называют центром симметрии геометрической фигуры в виде параллелограмма.
7. Точка пересечения диагоналей совпадает с отметкой, где пересекаются средние линии, которые по аналогии с диагональными отрезками делятся пополам.

Признаки

В процессе решения геометрических задач важно определить корректно разновидность исследуемой фигуры. Правильность идентификации многоугольника позволит применять свойства и закономерности для сокращения расчетов и оперативного вычисления величин. В случае параллелограмма предусмотрен ряд признаков. При выполнении одно из перечисленных условий можно сделать вывод о том, что остальные также соответствуют действительности:

• в четырехугольнике отсутствуют самопересечения, а пара противолежащих сторон взаимно параллельны и обладают равными величинами, то есть AB=CD, \(AB\parallel CD\);
• углы, расположенные напротив друг друга имеют равные градусные меры, к примеру, \(\angle A=\angle C,\angle B=\angle D\);
• многоугольник с четырьмя углами не имеет самопересечений, но содержит попарно соответствующие стороны, изображенные напротив друг друга, то есть AB = CD, BC=DA;
• пары противолежащих сторон являются параллельными отрезками, например, \(AB \parallel CD, BC \parallel DA\);
• диагональные линии, пересекающиеся в определенной точке, поделены этой отметкой на равные части, то есть AO=OC, BO=OD;
• в сумме расстояния между средними точками противолежащих сторон выпуклого четырехугольника составляют величину, которая равна половине периметра рассматриваемой фигуры;
• в сумме диагонали, возведенные в квадрат, соответствуют результату сложения размеров сторон во второй степени, к примеру, \(AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}\) .

Примеры решения задач

Решение

По условию задания задан параллелограмм. Обозначим его за АВСD. На первом этапе вычислений следует обратиться к свойствам этой фигуры. Из теоретического курса геометрии известно, что противолежащие стороны в таком четырехугольнике обладают равными величинами. Исходя из соотношения отрезков, описанных в примере, составим следующее равенство:

ВС = АВ + 5

Запишем формулу для определения периметра параллелограмма с учетом выражения, представленного выше:

АВ + ВС + СD + АD = АВ + АВ + 5 + АВ + АВ + 5 = \(4 \cdot АВ + 10 = 15\)

Из полученного соотношения выразим АВ и выполним соответствующие расчеты для определения стороны заданного параллелограмма с минимальной длиной:

\(АВ = \frac{15-10}{4} = 1,25\)

Ответ: 1,25.

Решение

В процессе решения этого задания целесообразно воспользоваться формулой для расчета площади геометрической фигуры в виде параллелограмма через процедуру умножения основания на высоту, которая проведена к заданному основанию. Используя озвученное соотношение, составим уравнение, применительно к условиям задачи:

\(35 = ВЕ \cdot AD = 5 \cdot (5 + АЕ)\)

В результате несложных математических вычислений получим, что:

АЕ = 2

Ответ: 2.

Решение

Путем построения диагонального отрезка, расположенного под прямым углом к стороне параллелограмма, образован прямоугольный треугольник. Воспользуемся теоремой Пифагора, чтобы определить величину отрезка АВ. Запишем соответствующее соотношение:

\(АВ^{2} = AD^{2} - BD^{2} = 25 – 16 = 9 \Rightarrow АВ = 3\)

Зная длину диагонального отрезка и сторону несложно рассчитать площадь параллелограмма:

\(S = 4 \cdot 3 = 12\)

Ответ: 12.