Что такое стереометрия в геометрии
Понятия стереометрии
Стереометрия представляет собой раздел в науке геометрии, нацеленный на исследование свойств, которые характерны для фигур, расположенных в пространстве.
Ознакомимся с основными понятиями и теориями данной области научных знаний. Предмет изучает разнообразные фигуры. Рассмотрим основные из них, с которыми часто можно столкнуться в процессе решения задач и в продолжении обучения темам из курса стереометрии повышенного уровня сложности.
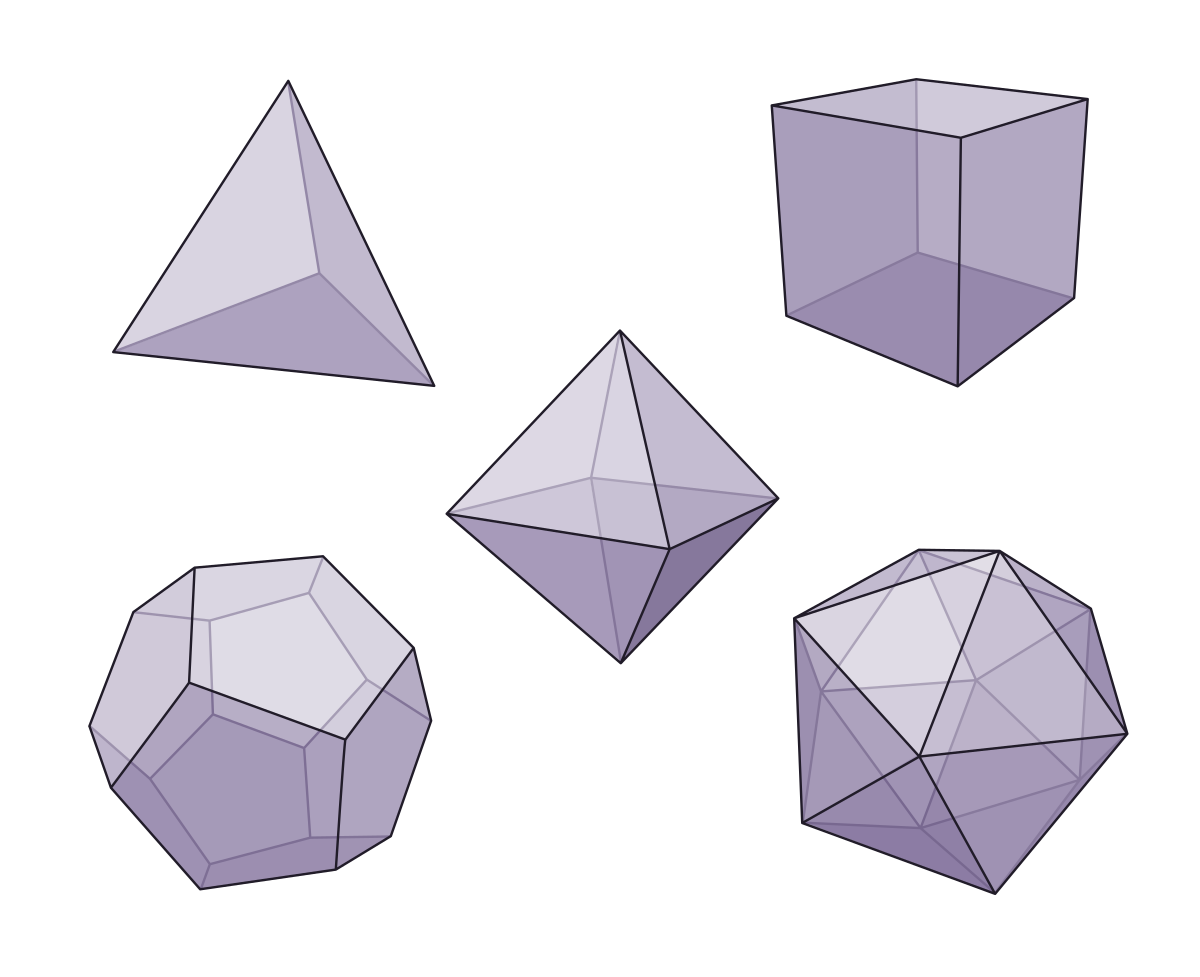
Многогранником называют некое тело в геометрии, границы которого сформированы с помощью определенного количества плоских многоугольников, какая-либо пара из которых обладает единой стороной и не расположена в общей плоскости.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Многогранники имеют следующие составные элементы:
- грани в виде многоугольников, которые упоминаются в определении;
- стороны, то есть ребра рассматриваемого многогранника;
- вершины, которые совпадают с вершинами данного многогранника.
Примеры многогранников:
Источник: ru.abcdef.wiki
Поверхность многогранника представляет собой фигуру, которая сформирована с помощью каждой из граней этого многогранника. При этом площади граней рассматриваемой фигуры в сумме дают площадь полной поверхности.
Кубом называют такой многогранник, который состоит из 6 граней в виде идентичных квадратов.
Куб обладает следующими компонентами:
- стороны являются ребрами фигуры;
- вершинами обозначают вершины рассматриваемого куба.
Пример куба:
Источник: pngwing.com
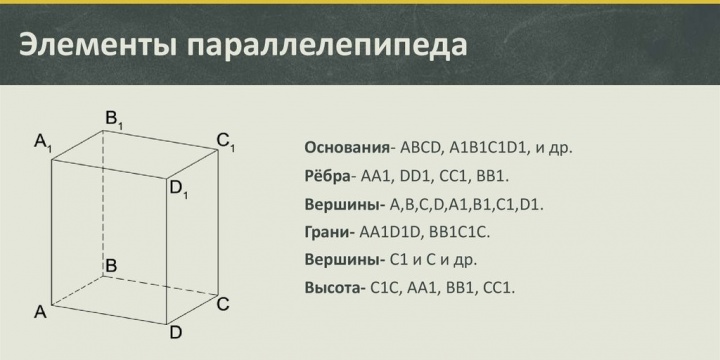
Параллелепипед является одним из видов многогранника, обладает 6 гранями в форме параллелограмма.
Перечислим компоненты параллелепипеда:
- стороны, то есть ребра;
- вершины, то есть вершины этих сторон.
Источник: 900igr.net
В прямом параллелепипеде грани с боков являются прямоугольниками. Прямоугольным называют такой параллелепипед, у которого каждая из граней обладает формой прямоугольника.
Призма представляет собой разновидность многогранника с парой граней в виде идентичных многоугольников и остальными гранями, изображенными, как параллелограммы.
Введем определения для элементов призмы:
- основания, то есть многоугольники, которые равны между собой;
- боковые грани в виде параллелограммов.
Призма может быть следующих типов:
- прямая, с боковыми гранями в форме прямоугольников;
- правильная, в виде прямой призмы, в основаниях которой расположены правильные многоугольники.
Пример призмы:
Источник: commons.m.wikimedia.org
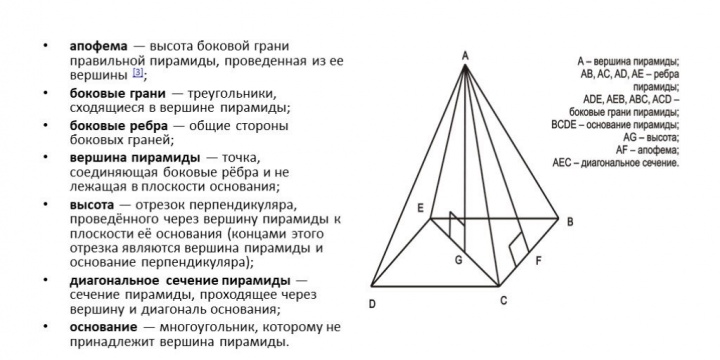
Пирамидой называют многогранник с одной гранью в виде некого многоугольника и остальными гранями, изображенными в форме треугольников, обладающих единой вершиной.
В состав пирамиды включены такие элементы, как:
- основание, то есть многоугольник;
- боковые грани треугольной формы;
- вершина, совпадает с единой вершиной треугольников.
Условия идентификации правильной пирамиды:
- в основании расположен правильный многоугольник;
- равенство боковых ребер.
Пример пирамиды:
Источник: fb.ru
Тетраэдр представляет собой треугольную пирамиду с гранями, изображенными в форме правильных треугольников, которые равны друг другу.
Источник: en.m.wikipedia.org
Аксиомы стереометрии и следствия из них
Упростить решение множества задач и изучение стереометрии позволяет знание основных положений и правил. К примеру, существуют аксиомы, которые не нуждаются в доказательстве. С их помощью достаточно просто выполнять построение классических и сложных фигур, производить разнообразные вычисления. Перечислим их.
Аксиома 1: Если 3 точки не принадлежат общей прямой, то через них допустимо построить плоскость в единственном экземпляре.
Аксиома 2: При нахождении 2 точек какой-то прямой в некой плоскости можно сделать вывод о расположении в этой же плоскости остальных точек рассматриваемой прямой.
Аксиома 3: В том случае, когда пара плоскостей обладает общей точкой, можно сделать вывод о наличии у таких плоскостей одной прямой, содержащей каждую из точек пересечения рассматриваемых плоскостей.
Аксиома 4: В какой-либо пространственной плоскости справедлива каждая из аксиом планиметрии.
При анализе перечисленных аксиом можно сформулировать некоторые закономерности. Такие утверждения называют следствиями. Перечислим их.
Если имеется какая-то прямая и точка, ей не принадлежащая, то через данные элементы допустимо провести единственную плоскость.
Если 2 прямые линии пересекаются между собой, то с их помощью допустимо построить единственную плоскость.
В том случае, когда имеется пара прямых, расположенных параллельно относительно друг друга, через них допустимо провести единственную плоскость.
Когда прямая не расположена на некоторой плоскости, данные элементы обладают максимум одной единой точкой.
Теоремы стереометрии
С помощью теорем стереометрии выявлены такие свойства фигур, которые позволяют значительно упростить решение примеров. Благодаря доказанным закономерностям, получается выполнить точные расчеты параметров изучаемых объектов. Рассмотрим основные из них.
О параллельности прямых и плоскостей
Параллельными называют прямую линию и некую плоскость, когда они не обладают едиными точками.
Представим, что имеется какая-то прямая а и произвольная плоскость \beta. При условии их параллельности можно составить следующее соотношение:
\(а \parallel \beta\)
Прямая линия АВ параллельна относительно некой плоскости Р, когда эта прямая расположена параллельно прямой СД, принадлежащей рассматриваемой плоскости.
В том случае, когда плоскость Р пересекает прямую АВ, которая расположена параллельно по отношению ко второй плоскости С, и эти плоскости имеют общую линию пересечения CD, эта линия проходит параллельно относительно прямой АВ.
При параллельности пары плоскостей Р и Q, которые пересекает другая плоскость R, можно заключить, что линии пересечения, образованные в результате, расположены параллельно друг другу.
При параллельности пары прямых АВ и DС, которые пересекаются между собой, неким другим прямым А1В1 и D1С1, расположенным на второй плоскости, рассматриваемые плоскости параллельны друг другу.
О перпендикулярности прямых и плоскостей
Перпендикулярное расположение прямой АВ относительно какой-то плоскости Р возможно при условии перпендикулярности рассматриваемой прямой паре каких-то прямых CD и EF, которые не являются параллельными, но принадлежат данной плоскости.
Представим, что прямая DE принадлежит некой плоскости Р и проходит через основание наклонной АС. Рассматриваемая прямая расположена перпендикулярно относительно этой плоскости при условии перпендикулярности данной прямой по отношению к проекции ВС, наклонной к плоскости Р.
При перпендикулярном расположении пары прямых АВ и CD относительно плоскости Р, данные прямые расположены параллельно относительно друг друга.
При перпендикулярности пары плоскостей Р и Q некой прямой АВ, данные плоскости расположены параллельно относительно друг друга.
О перпендикулярности плоскостей
Перед тем, как сформулировать следующие теоремы, полезно ввести понятия рассматриваемых в дальнейшем углов. К примеру, двугранный угол является прямым при условии, что его линейный угол прямой. Заметим равенство прямого двугранного угла и смежного с ним двугранного угла.
Две произвольных плоскости являются перпендикулярными между собой при условии образования с их помощью прямых двугранных углов.
Теорема о перпендикулярных прямых в пространстве: при пересечении пары прямых, которые расположены параллельно по отношению к паре перпендикулярных прямых, рассматриваемые прямые аналогично являются перпендикулярными друг другу.
Признак, согласно которому идентифицируют перпендикулярно расположенные прямую и плоскость: при перпендикулярности прямой паре прямых, которые пересекаются между собой и расположены на некоторой плоскости, рассматриваемая прямая проходит параллельно относительно данной плоскости.
Пусть имеется пара плоскостей, которые расположены перпендикулярно относительно друг друга. При построении перпендикуляра из какой-либо точки первой плоскости он будет расположен во второй плоскости.
При перпендикулярности пары пересекающихся плоскостей некой третьей плоскости линия пересечения является перпендикуляром к рассматриваемой плоскости.
О скрещивающихся прямых
Скрещивающиеся прямые представляют собой пару прямых, которые не принадлежат общей плоскости.
При расположении одной из пары прямых в какой-то плоскости и пересечении данной плоскости второй прямой в точке, которая не принадлежит первой прямой, рассматриваемые прямые допустимо назвать скрещивающимися.
Если имеются две скрещивающиеся прямые, которые пересекает плоскость, эта плоскость располагается параллельно по отношению к другой прямой и является единственной.
О трех перпендикулярах
Какая-либо прямая, которая расположена в некой плоскости перпендикулярно по отношению к проекции наклонной на данную плоскость, является перпендикулярной к самой наклонной.
Некоторая прямая, которая расположена в какой-то плоскости перпендикулярно относительно наклонной, является перпендикулярной и ее проекции на данную плоскость.
Взаимное расположение прямых в пространстве
При решении многих задач пригодится знание о расположении прямых в пространстве. Это важно для построения фигур в стереометрии и проведении различных вычислений. Рассмотрим возможные варианты построения прямых, которые могут принадлежать лишь одной плоскости или располагаться в разных плоскостях:
- Параллельные прямые в каком-то пространстве расположены в одной плоскости и не обладают едиными точками.
- Пара прямых в рамках какого-то пространства пересекается в том случае, когда при расположении в одной плоскости у них имеется общая точка.
- Скрещивающимися прямыми в пространстве называют такие прямые, которые не расположены в одной плоскости.
Стереометрия — фигуры
Из курса стереометрии можно узнать о многих фигурах. Такие объекты легко идентифицировать с помощью особых признаков, на основании которых сформулированы их определения. Кроме того, каждая из подобных фигур обладает рядом полезных свойств, упрощающих решение разнообразных задач.
Призма
В призме, то есть некотором многограннике, пара граней представляет собой идентичные многоугольники, которые расположены в параллельных друг другу плоскостях. Другие же грани призмы имеют форму параллелограммов. Данные фигуры обладают общими сторонами.
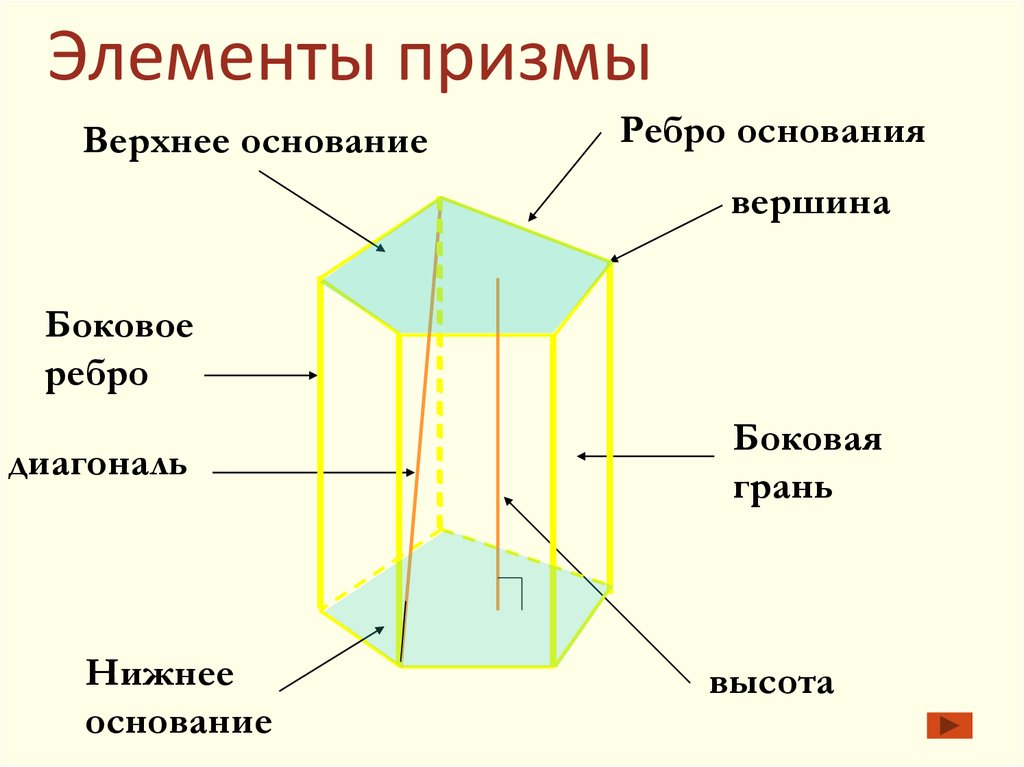
Обозначение элементов призмы:
Источник: ppt-online.org
Призма характеризуется следующими свойствами:
- основания определены, как многоугольники, равные между собой;
- боковые грани фигуры представляют собой параллелограммы;
- боковые ребра расположены параллельно относительно друг другу и являются равными.
Параллелепипед
Если в основании некой призмы расположен параллелограмм, то такая фигура носит название параллелепипеда. В зависимости от конфигурации, параллелепипеды бывают следующих видов:
- прямой;
- наклонный.
При условии, что в основании прямого параллелепипеда расположен прямоугольник, такую фигуру допустимо назвать прямоугольным параллелепипедом, каждая из граней которого представляет собой прямоугольник.
Обозначение элементов параллелепипеда:
Источник: ppt-online.org
Перечислим свойства, характерные для параллелепипеда:
- грани, расположенные напротив друг друга, являются равными и взаимно параллельными;
- все 4 диагонали обладают одной точкой пересечения, которая делит их на две равные части;
- боковые грани являются прямоугольниками, если параллелепипед прямой.
Пирамида
Пирамидой называют многогранник, если выполняются следующие условия:
- основание является многоугольником;
- другие грани имеют треугольную форму;
- грани обладают общей вершиной.
Пирамиды различают в зависимости от количества углов. К примеру, бывают пирамиды треугольные, четырехугольные и прочие.
Обозначения элементов пирамиды:
Источник: prezentacii.org
Перечислим ключевые свойства пирамиды:
- равенство боковых ребер;
- одинаковый наклон боковых ребер относительно основания;
- проекция вершины в центр окружности, которая описана около основания;
- равенство высот каждой из боковых граней, опущенных из вершины, расположение высоты во внутренней области пирамиды;
- равенство всех двугранных углов, расположенных при основании;
- проекция вершины в центр окружности, которая вписана в основание;
- равенство высот каждой из боковых граней, опущенных из вершины, расположение высоты за пределами пирамиды;
- равенство двугранных углов, расположенных между боковыми гранями и плоскостью основания;
- проекция вершины в центр окружности, вневписанной в основание пирамиды.
Сфера и шар
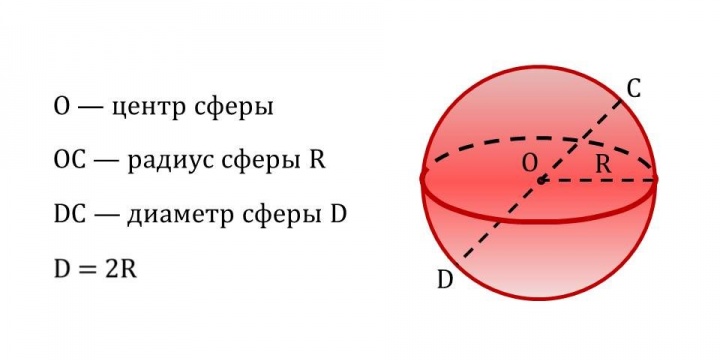
Сфера представляет собой замкнутую поверхность, геометрическое место точек в пространстве, расположенных на одинаковом расстоянии от точки, которая является центром сферы.
Согласно другому определению, сферой называют некое тело вращения, которое сформировано в результате вращательного движения полуокружности относительно собственного диаметра.
Элементы сферы:
Источник: urokimatematiki.ru
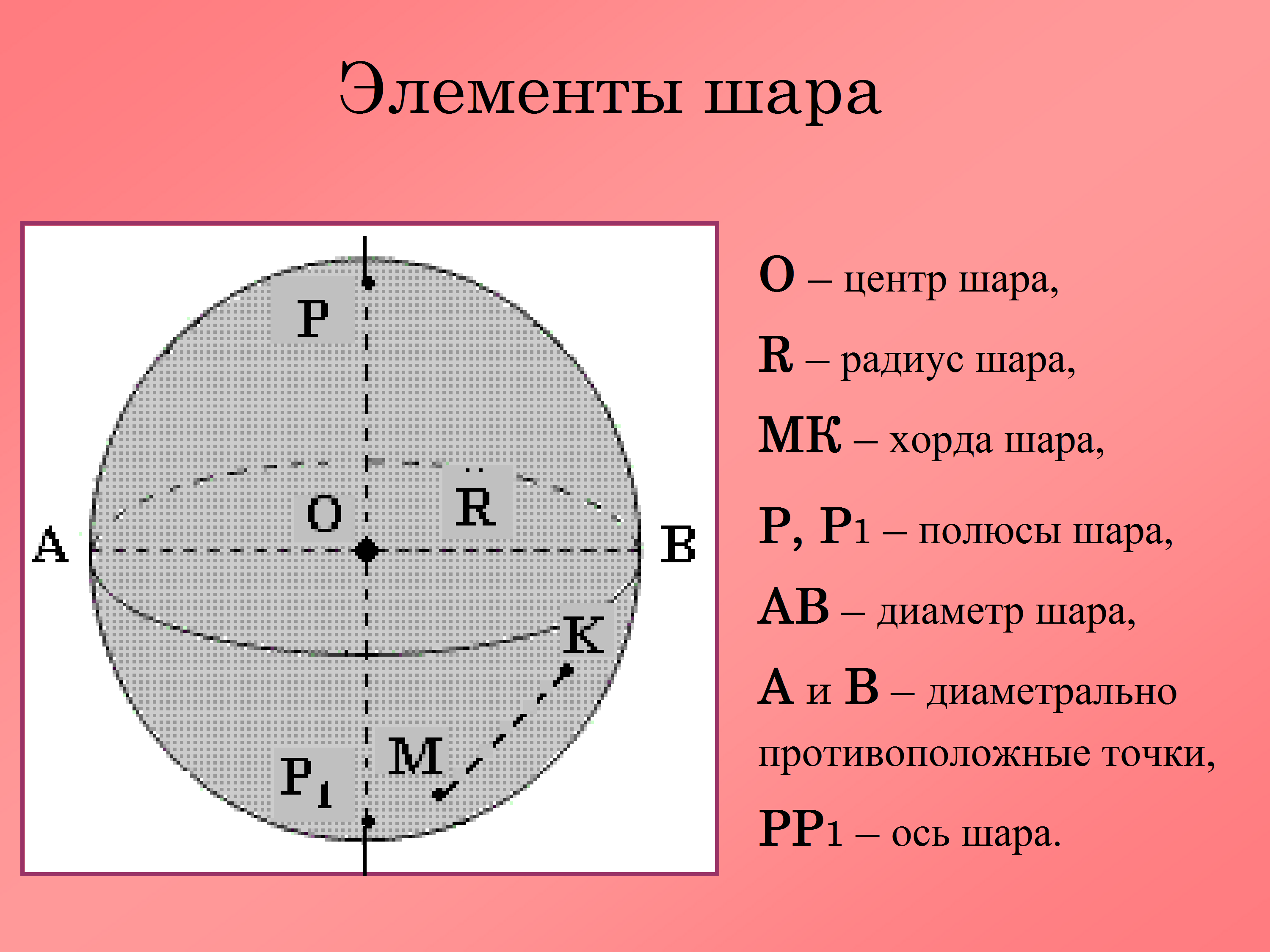
Шар является неким телом в геометрии, а также представляет собой совокупность всех точек в пространстве, расположенных на таком расстоянии, которое не превышает заданное от определенного центра. Данное расстояние носит название радиуса шара.
Получить шар можно, если вращать полукруг вокруг его стабильного диаметра. Заметим, что поверхность шара представляет собой сферу. Таким образом, шар — это геометрическое тело, в состав которого входит сфера и пространственная часть, ограниченная данной сферой.
Составные компоненты шара:
Источник: 900igr.net
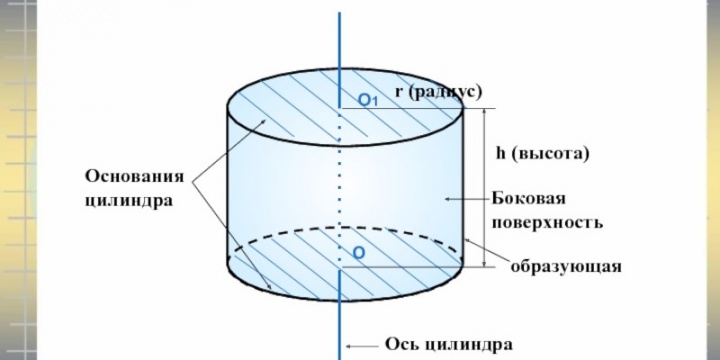
Цилиндр
Представим, что какая-то плоскость содержит окружность с центральной точкой, обозначенной за О, и радиусом R. Если построить прямые, проходящие через точки этой окружности и перпендикулярные ее плоскости, то в результате получится цилиндр.
Таким образом, можно сформировать цилиндрическую поверхность. Прямые, используемые при построении фигуры, являются образующими цилиндрической поверхности. Они параллельны, что следует из перпендикулярности данных прямых плоскости окружности.
Цилиндр представляет собой геометрическое тело, которое имеет ограничения в виде цилиндрической поверхности и двух плоскостей, которые расположены параллельно относительно друг друга и являются перпендикулярами к образующим цилиндрической поверхности.
Компоненты цилиндра:
Источник: theslide.ru
Цилиндр обладает следующими свойствами:
- равенство оснований;
- расположение оснований в плоскостях, которые параллельны друг другу;
- равенство и параллельность образующих цилиндра.
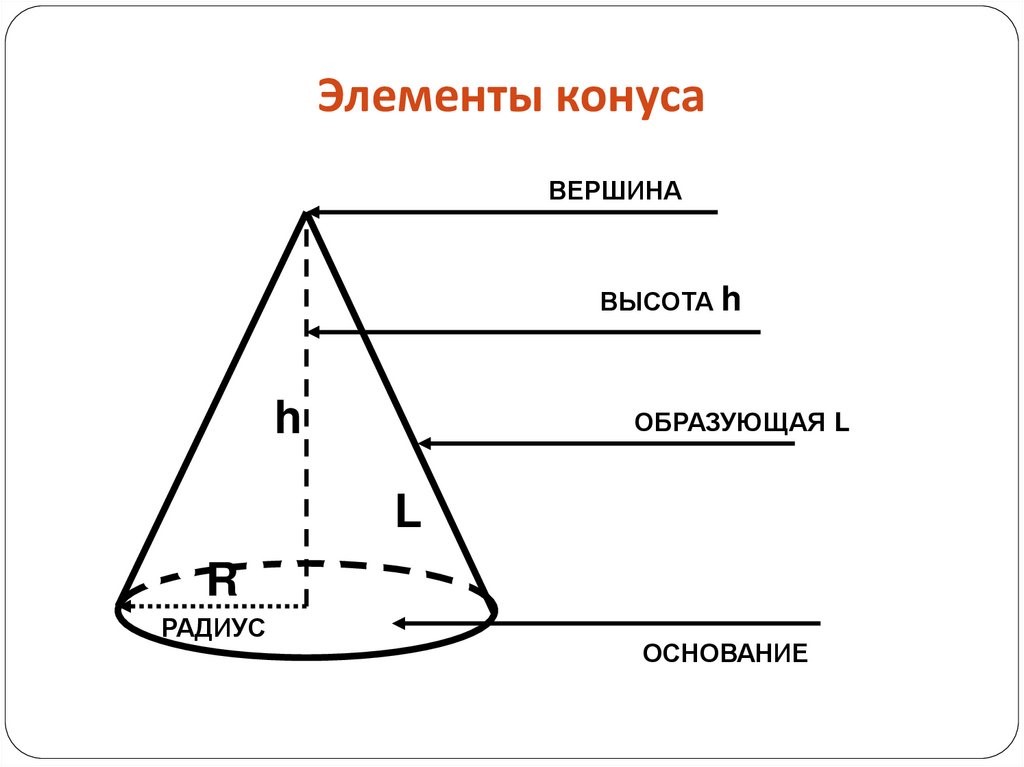
Конус
Конусом называют тело в геометрии, сформированное совокупностью всех лучей, которые выходят из некой точки и пересекают любую плоскую поверхность. На данном участке пересечения получается основание конуса.
Перечислим, какими элементами обладает конус:
Источник: ppt-online.org
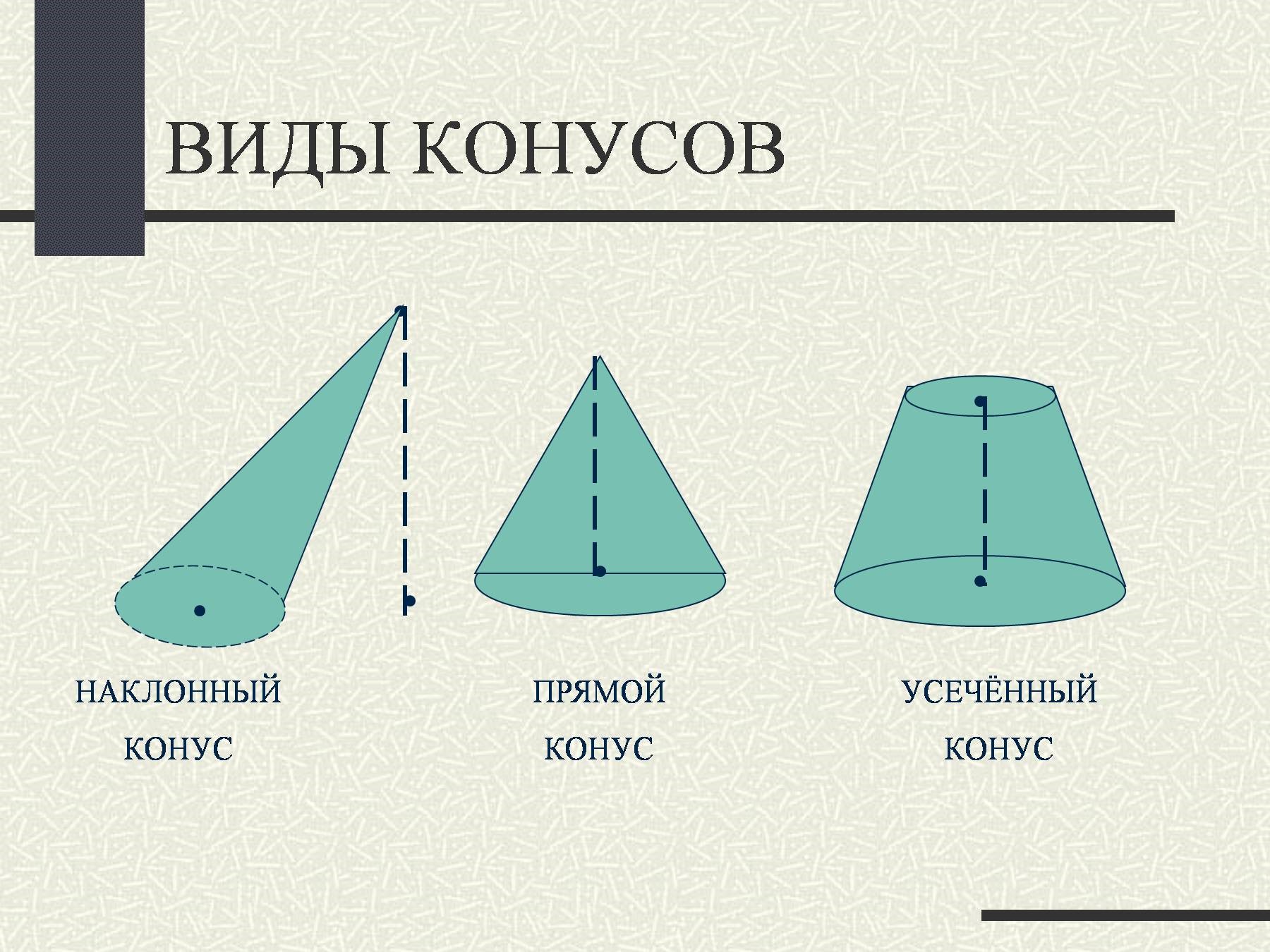
Разновидности конусов:
Источник: prezentacii.info
Перечислим свойства, которые характерны для конусов:
- равенство всех образующих прямого кругового конуса;
- образование прямого кругового конуса за счет вращения на полный круг прямоугольного треугольника относительно катета;
- образование прямого кругового конуса в результате вращения равнобедренного треугольника относительно собственной оси на половину круга;
- там, где конус пересекается с плоскостью, которая параллельно относительно его основания, формируется круг;
- когда при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, в области пересечения можно наблюдать образование эллипса;
- образование параболы можно наблюдать в месте пересечения при прохождении плоскости сечения через основание;
- прохождение плоскости сечения через вершину позволяет получить равнобедренный треугольник в области пересечения;
- центр тяжести какого-либо конуса расположен на 1/4 высоты от центральной точки основы.
Стереометрия — все формулы
При решении задач в стереометрии важно уметь вычислять площади поверхностей и объемы рассматриваемых фигур. В этом случае будут полезны следующие формулы.
Произвольная призма:
\(V=S{{\ }_{основания}}\cdot \text{H},\)
Здесь \({{\text{S}}_{основания}}\) обозначает площадь основания, H является высотой.
\({V}={{\text{S}}_{\bot }}\cdot l,\)
Здесь \({{\text{S}}_{\bot }}\) обозначает площадь сечения, которое перпендикулярно боковому ребру, l является длиной бокового ребра.
Площадь полной поверхности призмы складывается из всех площадей, которыми обладают ее грани.
\({{\text{S}}_{полн. пов.}}={{\text{S}}_{боков.пов.}}+2\cdot {{\text{S}}_{\text{основания}.}}\)
Прямая призма:
\({{\text{S}}_{боков.}}=\text{H}\cdot \text{P}\)
Здесь P обозначает периметр основания.
\({{S}_{полной\ \ \ }}=H\cdot P+2\cdot {{S}_{основания\ \ }}\)
Произвольная пирамида:
\({{S}_{полной\ \ \ }}=H\cdot P+2\cdot {{S}_{основания\ \ }}\)
Цилиндр:
\({{S}_{бок.}}=2\pi RH\)
\({{S}_{полн .}}=2\pi RH+2\pi {{R}^{2}}\)
Конус:
\({{S}_{бок.}}={{l}^{2}}\cdot \frac{\alpha }{2}\)
В данном случае \(\alpha\) является углом при вершине в радианах.
\({{S}_{бок.}}=\pi Rl\)
Здесь R является радиусом окружности основания, l обозначает длину образующей.
\({{S}_{полн. }}=\pi Rl+\pi {{R}^{2}}\)
\({{S}_{полн. }}=\pi R\left( l+R \right)\)
Шар, сфера:
\({{S}_{поверхности }}=4\pi {{R}^{2}}\)
Здесь R определяется, как радиус.
\({{S}_{поверхности }}=4\pi {{R}^{2}}\)
Правильный тетраэдр:
\(S={{a}^{2}}\sqrt{3}\)
Объем куба:
\(V=abc\)
Объем призмы:
\(V={{S}_{\text{основания}}}\ \ \ \ \cdot \text{H}\)
Объем пирамиды:
\(V=\frac{1}{3}{{S}_{\text{основания}}}\ \ \ \ \ \cdot \text{H}\)
Объем шара:
\({{V}_{\text{шара}}}\ \ \ \ \ =\frac{4}{3}\pi {{R}^{3}}\)
Здесь R обозначает радиус.
Объем цилиндра:
\(V=\pi {{R}^{2}}H\)
Здесь R обозначает радиус основания, H является высотой.
Объем конуса:
\(V=\frac{1}{3}\pi {{R}^{2}}H\)
Здесь R обозначает радиус основания, H является высотой.
Перечисленные формулы для нахождения элементов и параметров геометрических фигур часто используют в решении задач. С их помощью расчеты становятся компактнее и проще. Рассмотрим в качестве примера несколько типичных заданий.
На рисунке изображена треугольная пирамида SABC, которая является правильной. Обозначим ее вершину за S. Высота данной геометрической фигуры составляет \(2\sqrt3\) . Сторона основания равна 6. Требуется определить, чему равна градусная мера угла, расположенного между высотой и ребром SB.
Источник: shkolkovo.net
Решение
Заметим, что согласно условиям задачи рассматриваемая пирамида является правильной. На основании этого утверждения можно сделать вывод о равенстве основания геометрической фигуры правильному треугольнику. Таким образом, высота SO проходит через точку, в которой пересекаются медианы основания.
Представим, что медиана обозначена за \(ВВ_1\) . Этот резок также играет роль высоты. Воспользуемся теоремой Пифагора и запишем справедливое равенство:
\(BB_1=\sqrt{BC^2-B_1C^2}=3\sqrt3 \quad\Rightarrow\quad BO=\dfrac23BB_1=2\sqrt3\)
Вспомним из курсов геометрии о делении медиан с помощью точки пересечения в соотношении 2 к 1, начиная отсчет от вершины. В результате прямоугольный треугольник SOB допустимо считать равнобедренным. На основании этого заключения можно записать следующее равенство:
\(SO=BO=2\sqrt3\)
В результате градусная мера острых углов составит \(45^\circ.\)
Ответ: 45.
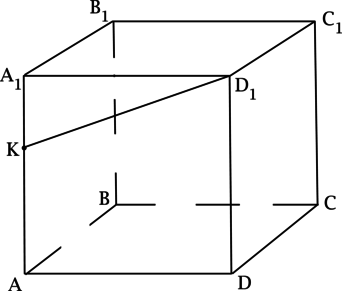
Имеется некий куб \(ABCDA_1B_1C_1D_1\) . Точка К расположена на ребре \(AA_1\) . Требуется определить градусную меру угла, находящегося между прямыми, которые содержат отрезки \(D_1K и AB\) .
Источник: shkolkovo.net
Решение
Заметим, что в кубе \(ABCDA_1B_1C_1D_1\) отрезок АВ является перпендикуляром, опущенным к плоскости \(ADD_1\). Исходя из данного утверждения, можно сделать вывод о перпендикулярности АВ какой-либо прямой, которая расположена в рассматриваемой плоскости \(ADD_1\) . На основании этого заключения сделаем вывод о равенстве искомого угла \(90^{\circ}\) .
Ответ: 90
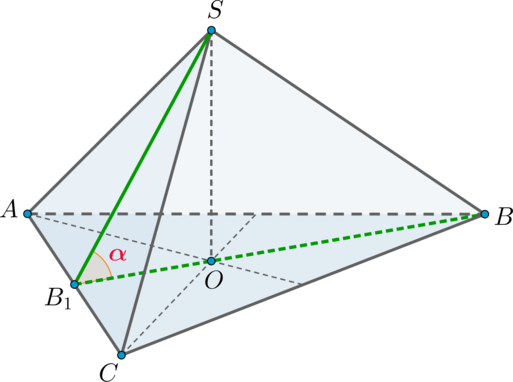
На рисунке представлена фигура в виде правильного тетраэдра, обозначенного за SABC. Требуется вычислить, чему равен тангенс во второй степени угла, который расположен между высотой грани SAC, проведенной из вершины S, и высотой грани ABC, выходящей из вершины B.
Источник: shkolkovo.net
Решение
Предположим, что \(SB_1\) играет роль высоты для грани SAC. Исходя из того, что в задании речь идет о геометрической фигуре в виде правильного тетраэдра, сделаем вывод о соответствии каждой из его граней правильному треугольнику. Данные треугольники равны между собой. В таком случае, \(SB_1\) , кроме прочего, представляет собой медиану. Из этого следует следующее соотношение:
\(AB_1=B_1C\)
Заметим, что в случае правильного тетраэдра его вершины являются началом высоты, проходящей через точку, в которой пересекаются медианы противолежащей грани. При этом SO играет роль высоты, точка О находится на пересечении медиан треугольника АВС. Исходя из этого, заключим, что в точке О пересекаются высоты по причине наличия правильного треугольника АВС.
Сделаем вывод о том, что \(BB_1\) является и медианой, и высотой. Согласно условию задания требуется вычислить \(\mathrm{tg}^2\angle (SB_1, BB_1)\). Обозначим буквой а ребро, принадлежащее тетраэдру. В таком случае:
\(BC=a\)
\(B_1C=0,5a\)
Воспользуемся записанным соотношением и применим к этой задаче теорему Пифагора. В результате получим, что:
\(BB_1=\sqrt{BC^2-B_1C^2}=\dfrac{\sqrt3}2a\)
Исходя из того, что в точке О пересекаются медианы, эта точка делит их в соотношении 2 к 1, если начинать отсчет от вершины. В результате:
\(OB_1=\frac13BB_1=\frac{\sqrt3}6a\)
Заметим, что справедливо следующее равенство:
\(\triangle ABC=\triangle SAC\)
Таким образом:
\(SB_1=BB_1\)
Рассмотрим прямоугольный треугольник \(SB_1O\) :
\(\cos \alpha=\dfrac{OB_1}{SB_1}=\dfrac13 \quad\Rightarrow\quad \sin \alpha =\sqrt{1-\cos^2\alpha}=\dfrac{2\sqrt2}3 \quad\Rightarrow\quad \mathrm{tg}^2\alpha=(2\sqrt2)^2=8.\)
Ответ: 8
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так