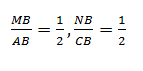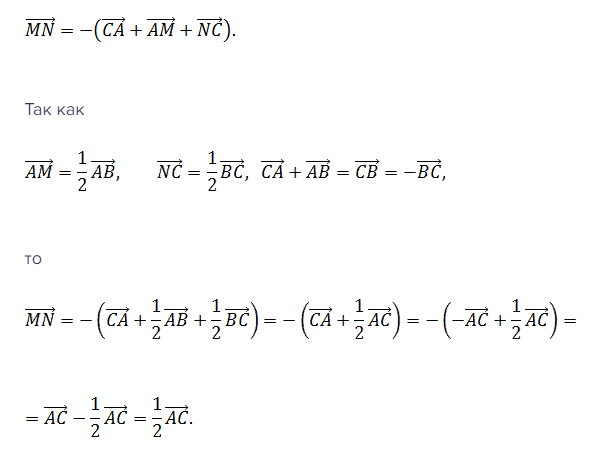Что нужно знать о средней линии треугольника — основные сведения
Использование понятия «средняя линия треугольника» помогает решить многие задачи по геометрии. Ее можно провести в любом треугольнике, независимо от соотношения длин его сторон и видов имеющихся углов.
Определение средней линии треугольника
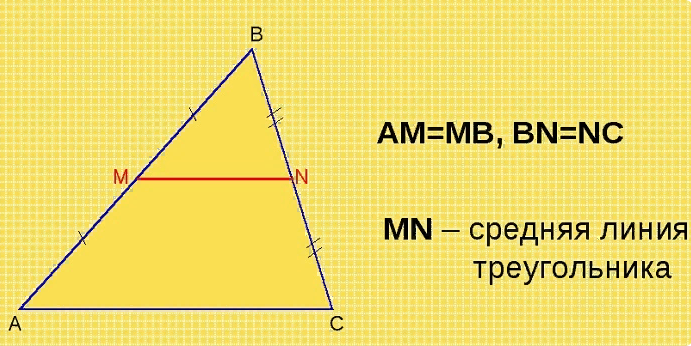
Средней линией треугольника называется отрезок, который располагается внутри него таким образом, что соединяет точки, являющиеся серединами двух сторон, лежащих противоположно.
Такое определение не является единственным. Исходя из доказательства теоремы Фалеса:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если отрезок, начинающийся на середине одной из сторон треугольника, заканчивается на другой стороне и параллелен третьей, то это средняя линия этого треугольника.
В любом треугольнике можно провести три срединные линии, поскольку он имеет три стороны, в т.ч. две — лежащие друг против друга.
Доказательством этого утверждения является теорема Фалеса:
Средняя линия треугольника — свойства, признаки и формулы
Cвойства средних линий могут различаться. Так, в прямоугольном треугольнике две из трех средних линии перпендикулярны катетам. В то же время третья — по длине аналогична медиане, которую провели к гипотенузе.
Для треугольника, имеющего острые углы и стороны различной длины, средние линии таким свойством не обладают.
Для прямоугольного треугольника является справедливым утверждение, что его средняя линия делит площадь на 4 треугольника, имеющие прямые углы.
В геометрии к свойствам средней линии относят:
- Найти длину средней линии можно разделив длину основания пополам. При этом основание треугольника и его средняя линия являются параллельными.
- Проведя в треугольнике среднюю линию, можно смело утверждать, что он отсек еще один треугольник, который с коэффициентом ½ подобен основному — большому. Вычислить его площадь можно, разделив площадь основного треугольника на 4.
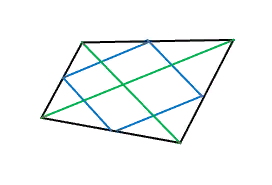
- Проведя в треугольнике все три средние линии, получают четыре треугольника равной площади. При этой центральный из них получил название дополнительного.
- Три средние линии, проведенные в прямоугольном треугольнике, также делят его на 4 меньших треугольника. При этом все они имеют прямые углы.
Из приведенного списка позволяет находить длину средней линии через длину стороны, которая ей параллельна.
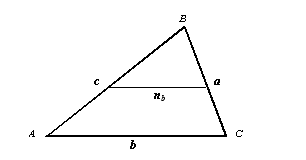
Рассмотрим треугольник: Формулу для такого действия, исходя из ниже приведенной схемы, можно выразить так:
Формулу для такого действия, исходя из выше приведенной схемы, можно выразить так:
nb=1/2b
Это же свойство № 1 лежит в основе следующей формулы — для нахождения площади треугольника, который образуется в результате отсекания части основного средней линией (S1) нужно площадь основного треугольника (S) разделить на 4:
S1=S/4
Теорема о средней линии треугольника
Утверждение, что средняя линия треугольника параллельна его основанию (либо третьей стороне) и по длине составляет половину этого основания, носит название теоремы о средней линии. Доказать ее можно с помощью трех способов:
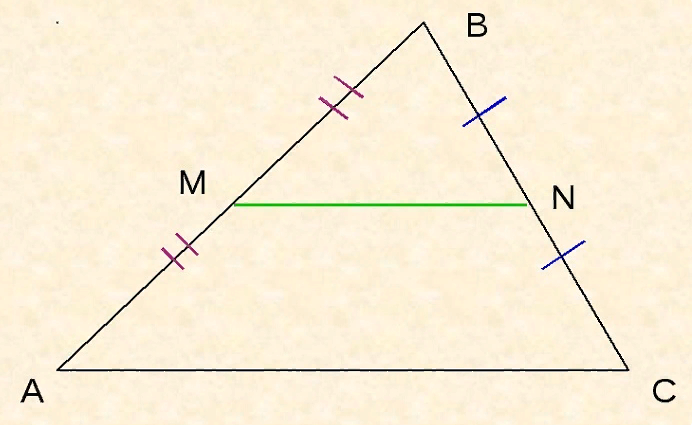
- Рассмотрим треугольник.
Из рисунка видно, что прямая MK параллельна AC. Исходя из теоремы Фалеса понятно, что точкой пересечения стороны BC является ее половина. Так как MN∈MK, значит MN параллельна AC.
Это доказательство первой части теоремы.
Приступаем к доказательству второй части: длина средней линии равна половине длины основания треугольника.
Предположим, что NP параллельна AB. По этому признаку она является средней линией треугольника (согласно теореме Фалеса). Если это так, то AP=PC.
Из рисунка видно, что фигура AMNP является параллелограммом, поэтому AP=MN. Из приведенных фактов следует, что MN=1/2AC
Второй способ основывается на том, что угол B — общий для треугольников MBN и ABC.
По известному признаку, лежащему в основе подобия треугольников, можно утверждать, что ΔMBN∼ΔABC.
Отсюда следует равенство углов BMN и BAC. Данные углы соответственные, поэтому прямые MN и AC являются параллельными.
Поскольку MN является средней линией треугольника, ее длина — равная половине AC.
Правильным является утверждение, что пропорциональность двух пар сторон обуславливает аналогичное отношение, касающееся третьей пары сторон.
Третий вариант доказательства теоремы средней линии использует такое понятие, как сумма векторов: CA, AM, MN, NC. Из вышеприведенного рисунка можно узнать, что последовательно сменяющие друг друга обозначенные векторы образуют замкнутую линию. Поэтому их сумма равна нулю.
Проведя простые математические действия, получаем формулу:
Для решения задач по нахождению параметров равнобедренных, равносторонних, прямоугольных треугольников важно знать следствия из теоремы средней линии. К ним относятся:
- С помощью средней линии можно отсечь в основном треугольнике второй, меньший по размеру, но подобный треугольник. Его площадь составляет четверть основного, а коэффициент подобия равен ½.
Данное утверждение может быть доказано исходя из следующего:
Согласно своим особенностям средняя линия треугольника пересекается с двумя его сторонами в их серединах. Следовательно, она делит стороны AB и BC пополам. Можно записать, что MB/AB=BN/BC=1/2
В то же время сама теорема средней линии утверждает, что ее длина составляет половину основания (третьей стороны треугольника). Значит MN/AC=1/2
Искать продолжение доказательства следствия теоремы следует в третьем признаке подобия. Установлено, что площади фигур, являющихся подобными, относятся друг к другу как коэффициента подобия в квадрате. То есть приходим ко второй части свойства: площадь меньшего треугольника находится по отношению к площади большего как дробь ¼.
Поэтому записываем:
SΔMBN/SΔABC=1/4
Это результат, какой и следовало доказать.
Существует еще одно следствие из теоремы средней линии. Оно звучит следующим образом:
Если в треугольнике провести три средние линии, то они разделят его на четыре одинаковых по площади треугольника, которые будут подобными исходному с коэффициентом подобия 0,5.
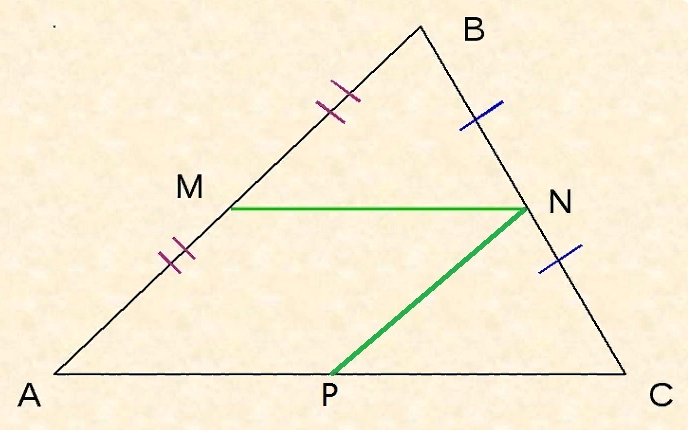
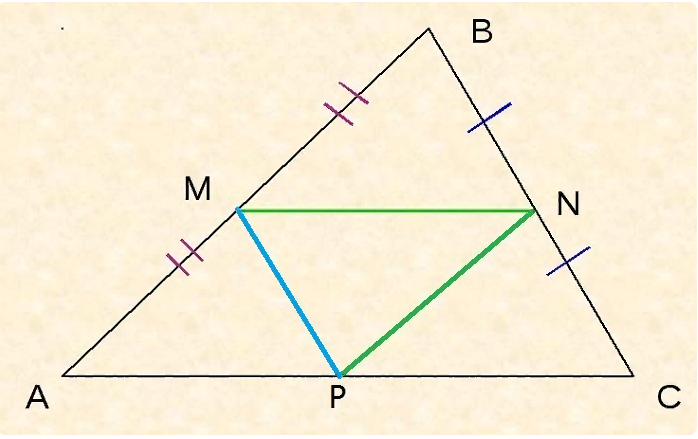
Для доказательства рассмотрим рисунок.
На рисунке отрезок MN является средней линией треугольника. Поэтому по одному из своих свойств он параллелен AC. Вытекающий признак: угол BMN равен углу BAP, а угол BNM равен углу BCA, поскольку они прилегают к параллельным прямым и линиям, которые являются секущими (AB и BC).
Аналогичная ситуация по линии MP. Она параллельна BC, откуда следует, что угол MPA равен углу BCA. Это углы соответственные с учетом параллельности прямых и секущей AC.
Из вышеприведенного следует, что углы BNM, BCA, MPA равны.
MN — средняя линия треугольника, поэтому ее длина составляет половину AC и равна AP.
Поэтому треугольники AMP и MBN равны (согласно второму признаку равенства).
Факт, что остальные пары треугольников равны, можно доказать аналогичным образом.
Треугольники MBN и ABС подобны с коэффициентом 0,5. Поскольку все образовавшиеся треугольники равны, то любой из них является подобным основному (большому) с одним и тем же коэффициентом.
Задачи на использование теоремы
Дан рисунок. Необходимо доказать, что в произвольном выпуклом четырехугольнике середины сторон — вершины параллелограмма.
При проведении диагонали в четырехугольнике образуется два треугольника. В обоих необходимо построить средние линии, которые по определению будут параллельными диагонали (являющейся основанием).
Существует правило: если две прямые параллельны третьей, то они параллельны между собой. В тот же время стороны, которые лежат противоположно и образованы средними линиями в 4-х угольнике, также параллельны.
Это и есть запрашиваемое по условию задачи доказательство.
Касательно параллельности двух других сторон вновь образованного 4-х угольника, то ее можно доказать аналогичным путем. Четырехугольник, который образовался в результате соединения середин сторон первоначально данного четырехугольника, называется параллелограммом.
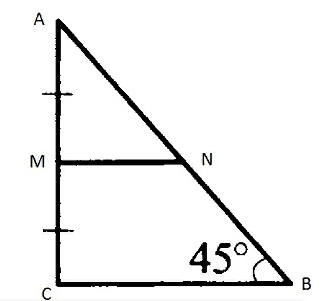
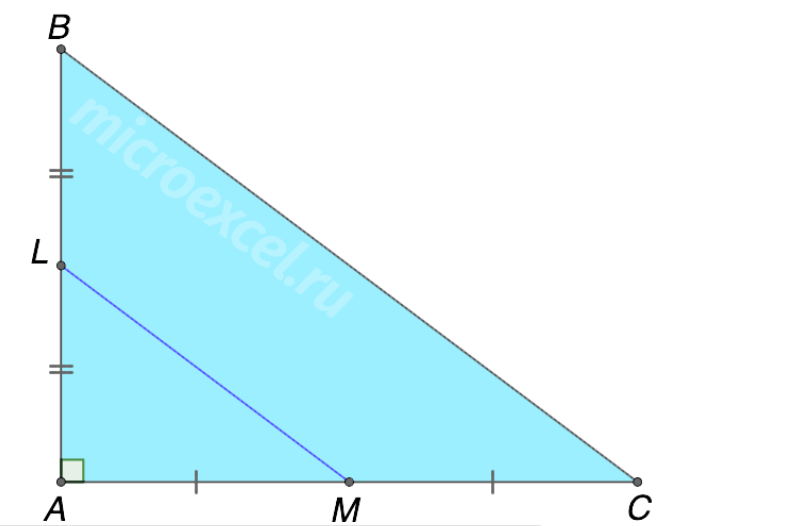
На рисунке изображен треугольник. Его сторона имеют длины 6 и 8 см. В треугольнике провели среднюю линию, соединив две стороны. Какой размер она имеет?
Изобразив схематически треугольник с заданными сторонами (катетами), видим, что он прямоугольный. По своему определению средняя линия, соединяющая эти катеты, параллельна основанию (гипотенузе) и составляет половину ее длины.
Для дальнейшего решения обратимся к теореме Пифагора, которая говорит: «для прямоугольного треугольника справедливо выражение: квадрат гипотенузы равняется сумме квадратов катетов».
Записываем данное утверждение математически применительно для имеющегося треугольника:
BC2=AB2+AC2=62+82=100
Проведя несложные вычисления, получаем ответ задачи:
BC=√100=10
Отсюда длина средней линии LM составляет половину длины BC и равна 10/2=5 см
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так