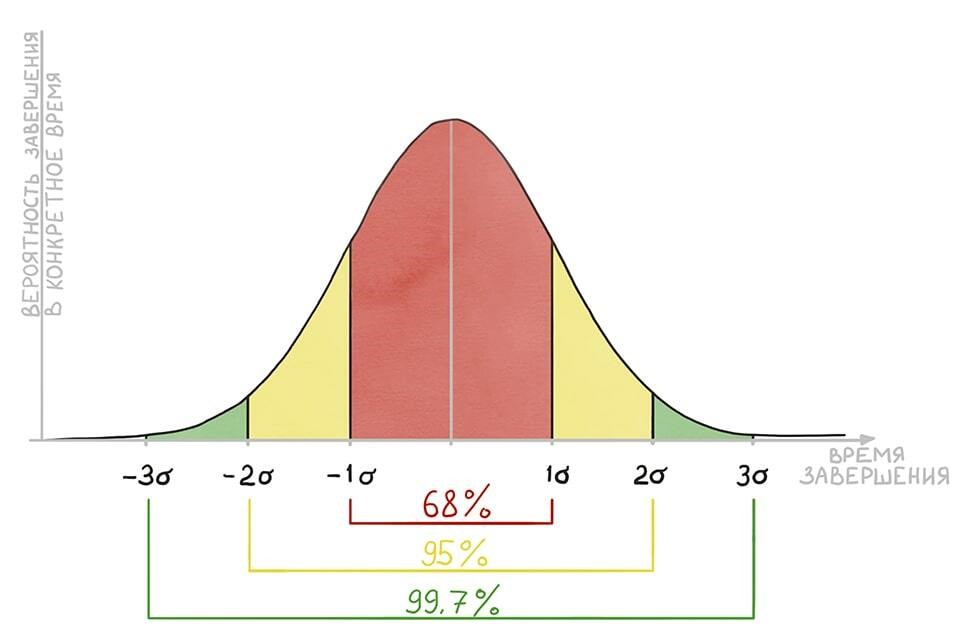
Среднее квадратическое отклонение

Среднеквадратичное отклонение — это

Дисперсия и среднеквадратичное или стандартное отклонение — важные показатели, используемые в математике и статистике для нахождения значения из большого набора данных. Различные формулы для дисперсии и среднеквадратичного отклонения широко используются в математике для определения тенденций различных величин в математике. Дисперсия — это мера того, как точки данных изменяются в зависимости от среднего значения, а стандартное отклонение — мера центральной тенденции распределения данных.

Основное различие заключается в единицах измерения. Стандартное отклонение измеряется в единицах, аналогичных единицам среднего значения данных, в то время как дисперсия измеряется в квадратных единицах.

Различные свойства дисперсии группы данных таковы:

1. Поскольку каждый член в формуле дисперсии сначала возводится в квадрат, а затем находится его среднее значение, оно всегда неотрицательно, т. е. среднее может быть как положительным, так и нулевым, но никогда не может быть отрицательным.
2. Дисперсия всегда измеряется в квадратных единицах. Например, если нам нужно найти дисперсию роста ученика в классе, и если рост ученика задан в см, то дисперсия вычисляется в см².

В проекте

Источник: tenchat.ru

Стандартное отклонение полезно при сравнении разброса двух отдельных наборов данных, имеющих примерно одинаковое среднее значение. Набор данных с меньшим стандартным отклонением имеет более узкий разброс измерений вокруг среднего значения и, следовательно, обычно имеет сравнительно меньше высоких и низких значений. Элемент, выбранный наугад из набора данных с низким стандартным отклонением, имеет больше шансов оказаться вблизи среднего значения, чем элемент из набора данных с более высоким стандартным отклонением. Однако на стандартное отклонение влияют экстремальные значения. Одно экстремальное значение может сильно повлиять на стандартное отклонение.

Стандартное отклонение может быть трудно интерпретировать с точки зрения того, насколько большим оно должно быть, если считать, что данные широко разбросаны. Величина среднего значения набора данных влияет на интерпретацию его стандартного отклонения. Когда вы измеряете что-то в миллионном масштабе, показатели, близкие к среднему значению, не имеют того же значения, что при измерении чего-то в сотенном масштабе. Например, измерение двух крупных компаний с разницей в годовом доходе в 10 000 долларов считается довольно близким, в то время как измерение двух людей с разницей в весе в 30 килограммов считается далеким. Вот почему в большинстве ситуаций полезно оценивать размер стандартного отклонения относительно среднего значения.

При использовании стандартного отклонения надо помнить о следующих свойствах:

1. Стандартное отклонение чувствительно к экстремальным значениям. Одно очень экстремальное значение может увеличить стандартное отклонение и исказить дисперсию.
2. Для двух наборов данных с одинаковыми средними значениями большее стандартное отклонение имеет тот набор, в котором данные сильнее разбросаны от центра.
3. Стандартное отклонение равно 0, если все значения равны (потому что тогда все значения равны среднему).

Применение

Стандартное отклонение широко используется в экспериментальных и промышленных условиях для проверки моделей на реальных данных. Примером такого применения в промышленности является контроль качества некоторых продуктов. Стандартное отклонение может быть использовано для расчета минимального и максимального значения, в пределах которого должен находиться некоторый аспект продукта в большом проценте случаев. В случаях, когда значения выходят за пределы рассчитанного диапазона, может потребоваться внести изменения в производственный процесс для обеспечения контроля качества.

Среднеквадратичное отклонение также используется в погоде для определения различий в региональном климате. Например, два города, один на побережье, а другой в глубине материка, в которых средняя температура составляет 22°C. Хотя это может натолкнуть на мысль, что температура в этих двух городах практически одинакова, реальность может быть замаскирована, если рассматривать только среднее значение, а стандартное отклонение игнорировать.

Прибрежные города, как правило, имеют более стабильную температуру из-за регулирования большими водоемами, поскольку вода обладает большей теплоемкостью, чем суша; по сути, это делает воду гораздо менее восприимчивой к изменениям температуры, и прибрежные районы остаются более теплыми зимой и более прохладными летом из-за количества энергии, необходимой для изменения температуры воды. Таким образом, в то время как в прибрежном городе температура может колебаться от 14 до 30°C в течение определенного периода времени, в результате чего средняя температура составит 22°C, во внутреннем городе температура может колебаться от -2 до 42°C, что приведет к той же средней температуре.

Еще одна область, в которой среднеквадратичное отклонение находит широкое применение, — это финансы, где оно часто используется для измерения риска, связанного с колебаниями цен на какой-либо актив или портфель активов. Использование стандартного отклонения в таких случаях позволяет оценить неопределенность будущих доходов от конкретной инвестиции. Например, если сравнивать акции A со средней доходностью 7% и стандартным отклонением 10% с акциями B, имеющими такую же среднюю доходность, но стандартное отклонение 50%, то первая акция явно будет более безопасным вариантом, поскольку стандартное отклонение акций B значительно больше при точно такой же доходности. Но это не значит, что акция А однозначно является лучшим вариантом инвестиций в этом сценарии, поскольку стандартное отклонение может исказить среднее значение в любую сторону. В то время как акции А имеют более высокую вероятность средней доходности, близкой к 7%, акции Б потенциально могут обеспечить значительно большую доходность (или убыток).

Как рассчитать, формула

Формула стандартного среднеквадратичного для популяции выглядит следующим образом:

σ2=1NN∑i=1(xi−μ)2 σ 2 = 1 N ∑ i = 1 N ( x i − μ ) 2.

где:

σ = стандартное отклонение популяции;

N = количество наблюдений в популяции;

Xi = i-ое наблюдение;

μ = среднее значение по популяции.

Аналогично, формула выборочного стандартного отклонения имеет вид:

s = ∑ ( X − X ¯ ) 2 n − 1

В формуле среднеквадратичного отклонения используются три переменные. Первая переменная — это значение каждой точки в наборе данных с суммой чисел, обозначающих каждую дополнительную переменную (x, x1, x2, x3 и т. д.). Среднее значение применяется к значениям переменной M и количеству данных, отнесенных к переменной n. Дисперсия — это среднее значение квадратов разностей от среднего арифметического.

Для расчета среднего значения необходимо сложить значения элементов данных и разделить полученную сумму на количество участвовавших в исследовании элементов данных.

Стандартное отклонение, обозначаемое символом σ, представляет собой квадратный корень из среднего квадрата всех значений ряда, полученных из среднего арифметического, которое также называется среднеквадратичным отклонением. 0 — наименьшее значение стандартного отклонения, поскольку оно не может быть отрицательным. Если элементы ряда более изолированы от среднего значения, то стандартное отклонение также велико.

Статистический инструмент стандартного отклонения — это мера дисперсии, которая вычисляет неустойчивость разброса данных. Например, среднее значение, медиана и мода — это показатели центральной тенденции. Поэтому они считаются центральными средними первого порядка. Меры дисперсии, которые упоминаются непосредственно над ними, представляют собой средние отклонения от средних значений, поэтому их называют средними второго порядка.

Примеры решения задач

Решение:

Учитывая стандартное отклонение, σ = 6,2.

Значит, дисперсия = σ2 = 6,22 = 38,44.

Следовательно, вариант (3) является ответом.

Первым шагом будет вычисление среднего значения. Сумма равна 33, а точек данных 5. Следовательно, среднее значение равно 33 ÷ 5 = 6,6. Затем возьмите каждое значение из набора данных, вычтите среднее и возведите разницу в квадрат. Например, для первого значения:

(2 - 6.6)2 = 21.16

Возведенные в квадрат разности для всех значений складываются:

21.16 + 0.16 + 12.96 + 29.16 + 5.76 = 69.20

Затем сумма делится на количество точек данных:

69.20 ÷5 = 13.84.

Дисперсия равна 13,84. Чтобы получить стандартное отклонение, нужно вычислить квадратный корень из дисперсии, который равен 3,72.

Решение:

Пусть xi: = 18, 22, 19, 25, 12;

Здесь n = 5;

Среднее (x̄) = (18 + 22 + 19 + 25 + 12)/5 = 96/5 = 19.2

Вычислим величину отклонений, то есть (xi - x̄).

(xi - x̄) = (18 - 19,2), (22 - 19,2), (19 - 19,2), (25 - 19,2), (12 - 19,2) = -1.2, 2.8, -0.2, 5.8, -7.2

Теперь возведем отклонения в квадрат.

(xi - x̄)2 = (-1,2)2, (2,8)2, (-0,2)2, (5,8)2, (-7,2)2 = 1.44, 7.84, 0.04, 33.64, 51.84

∑(xi - x̄)2 = 1,44 + 7,84 + 0,04 + 33,64 + 51,84 = 94.80

(1/n-1)∑(xi - x̄)2 = 94,80/4 = 23,7.

Решение:

Четные числа меньше 10 - это {0, 2, 4, 6, 8}.

Этот набор данных имеет пять значений (n) = 5

Прежде чем найти дисперсию, нужно найти среднее значение набора данных.

Среднее, x̅ = (0+2+4+6+8)/5 = 4

Мы можем подставить значение данных и среднее в формулу, чтобы получить;

σ2 = Σ (xi - x̅)2/n

⇒ σ2 = [(0-4)2 + (2-4)2 + (4-4)2 + (6-4)2 + (8-4)2]/5

⇒ σ2 = (16 + 4 + 0 + 4 + 16)/5 = 40/5

Дисперсия (σ2) = 8

Теперь стандартное отклонение (σ) = √ (σ2)

⇒ Стандартное отклонение (σ) = √(8);

⇒ Стандартное отклонение (σ) = 2,828.

Решение:

Все возможные исходы бросания кубика равны {1; 2; 3; 4; 5; 6}.

Этот набор данных имеет шесть значений (n) = 6

Прежде чем найти дисперсию, необходимо найти среднее значение набора данных.

Среднее, x̅ = (1+2+3+4+5+6)/6 = 3,5

Мы можем подставить значение данных и среднее в формулу, чтобы получить;

σ2 = Σ (xi - x̅)2/n

⇒ σ2 = [(1-3.5)2 + (2-3.5)2 + (3-3.5)2 + (4-3.5)2 + (5-3.5)2 + (6-3.5)2]/6;

⇒ σ2 = (6.25+2.25+0.25+0.25+2.25+6.25)/6.

Дисперсия (σ2) = 2,917.

Теперь,

Стандартное отклонение (σ) = √ (σ2);

⇒ Стандартное отклонение (σ) = √(2.917);

⇒ Стандартное отклонение (σ) = 1,708.