Алгоритм сокращения дробей

Любое математическое действие с дробями целесообразно проводить после приведения их к простому и компактному варианту. Для этого используется особый метод — сокращение. При этом действие должно касаться как числителя, так и знаменателя.

Что такое дробь

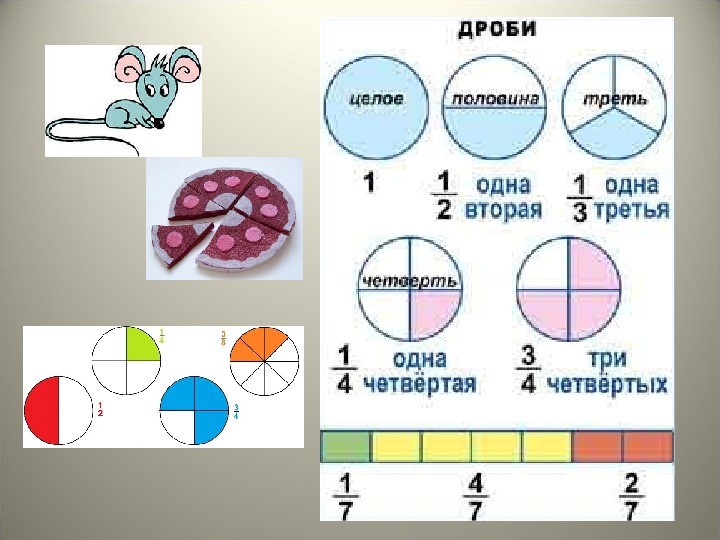
Если предмет разделить на несколько частей и взять несколько из них, то выразить такое действие можно дробью.

Выражается это так:

Источник: fs.znanio.ru

Вышеприведенные дроби являются обыкновенными и правильными, поскольку у них числитель меньше знаменателя. В противоположном случае такая дробь именуется неправильной. 

В обыкновенной дроби числитель и знаменатель являются целыми числами. Знаменатель никогда не может быть равным нулю.

Если знаменатель дроби равняется десяти либо десяти в какой-либо степени, такая дробь получила название десятичной и может записываться так: 3,4; 5,6. Равнозначными выражениями являются соответственно: ³⁴/₁₀; ⁵⁶/₁₀.

Впервые делать операции с дробями начали жители Древнего Египта. Разделив предмет на три части, они выражали взятую часть дробями типа 1/3, 2/3. Правда, более двойки в числителе у них никогда не было. Была выведена и универсальная простейшая формула для обозначения дроби: 1/n, где знаменатель обозначен буквой римского алфавита и мог принимать различные значения.

Действия с дробями неизменно присутствуют в математике и предполагают соблюдение правил их сокращения.

Правила сокращения дробей

Сокращение дроби применяется с целью придания ей простоты и облегчения алгебраических операций. Для понимания этого утверждения рассмотрим пример:

4 превратится в единицу, а 8 — в двойку, если их разделить на 4. В таких случаях говорят о сокращении дроби на 4.

Число, на которое происходит деление, называется общим делителем.

Источник: heslide.ru

Аналогичный результат получится, если числитель и знаменатель умножить на одно и тот же число. Только тогда не применяется термин «сокращение», поскольку при этом не происходит уменьшения обеих значений.

Сокращение дробей не является сложным действием, однако требует знания алгоритма его проведения. Он состоит из этапов:

• определить наименьший общий делитель для числителя и знаменателя (НОД);
• произвести деление обеих частей дроби на НОД.

В результате таких действий можно легко сокращать дробь, приводя ее к более простому и компактному значению.

Сокращая числитель и знаменатель на 11, получаем равенство: 55/88=5/8

В этом примере 11 — наименьший общий делитель.

Это поэтапное сокращение.

Гораздо удобнее сразу найти НОД:

16/64=(1*16)/(4*16)=1/4

Десятичных

С помощью сокращения можно решать и примеры с десятичными дробями.

Как было сказано выше, десятичная дробь — это та, у которой знаменатель представлен десяткой либо десяткой в какой-либо степени.

Сокращение таких дробей заключается в отбрасывании нулей, стоящих после последнего числового знака, стоящего после запятой.

Согласно данному правилу, 5,4=5,40 или 2,66=2,66000.

Действием, противоположным сокращению десятичной дроби, является ее расширение.

В качестве примера рассмотрим задание, как расширить десятичную дробь 0,003. Необходимо увеличить количество числовых знаков после запятой путем добавления нулей.

Решение: 0,003=0,00300.

В результате обоих действий наблюдается равнозначность дробей до и после сокращения (расширения).

В математике сокращение десятичных дробей рассматривается и с другой стороны. Для этого дробь необходимо записать в виде обыкновенной, имеющей числитель и знаменатель. После этого произвести сокращение, описанное выше.

Например: 0,25=25/100=1/4

В математике сокращение десятичных дробей рассматривается и с другой стороны. Для этого дробь необходимо записать в виде обыкновенной, имеющей числитель и знаменатель. После этого произвести сокращение, описанное выше.

Например: \(0,25=25/100=1/4\)

\(5,4=54/10=52/5\)

\(8,6=86/10=82/5\)

Неправильных

Для такой дроби частное от деления числителя на знаменатель меньше единицы либо равно ей.

Например, неправильными дробями являются ⁵/₄, ⁸/₆, ⁹/₉, ⁶/₃.

Сокращение неправильных дробей происходит таким же образом, что и правильных:

1. Найти НОД.
2. Разделить числитель и знаменатель на найденный НОД.
3. Записать дробь в виде правильной (либо десятичной), если того требует условие задачи.

Математическая запись такого действия следующая: \(8/6=(2*4)/(2*3)=4/3=11/3\)

Обыкновенных

Сокращение обыкновенных дробей рассмотрим на примере, в котором оно может проходить в несколько этапов:

Для числителя и знаменателя дроби проведем их разложение на множители: \(144/288=(12*12)/(12*24)\)

Сократим числитель и знаменатель на общий множитель — 12.

Дробь превращается в \(12/24\).

Полученная дробь не является несократимой, поэтому еще раз разложим ее на множители: \(12/24=(2*6)/(2*12)=6/12\)

И эта дробь не является несократимой. Повтори действие снова:

\(6/12=(1*6)/(2*6)=1/2\)

Данная дробь является несократимой. Следовательно, сокращение проведено полностью.

Источник: cf2.ppt-online.org

Сократить количество необходимых действий поможет использование принципа нахождения наименьшего общего делителя, описанного выше.

Сложных

По-другому такая дробь называется многоэтажной.

Источник: mydocx.ru

Из рисунка видно, что в зависимости от того, насколько правильно определена главная дробная черта, зависит результат превращения сложной дроби в простую.

Таким образом, работа со сложными дробями заключается в приведении ее к модели обычной с дальнейшим сокращением.

Смешанных

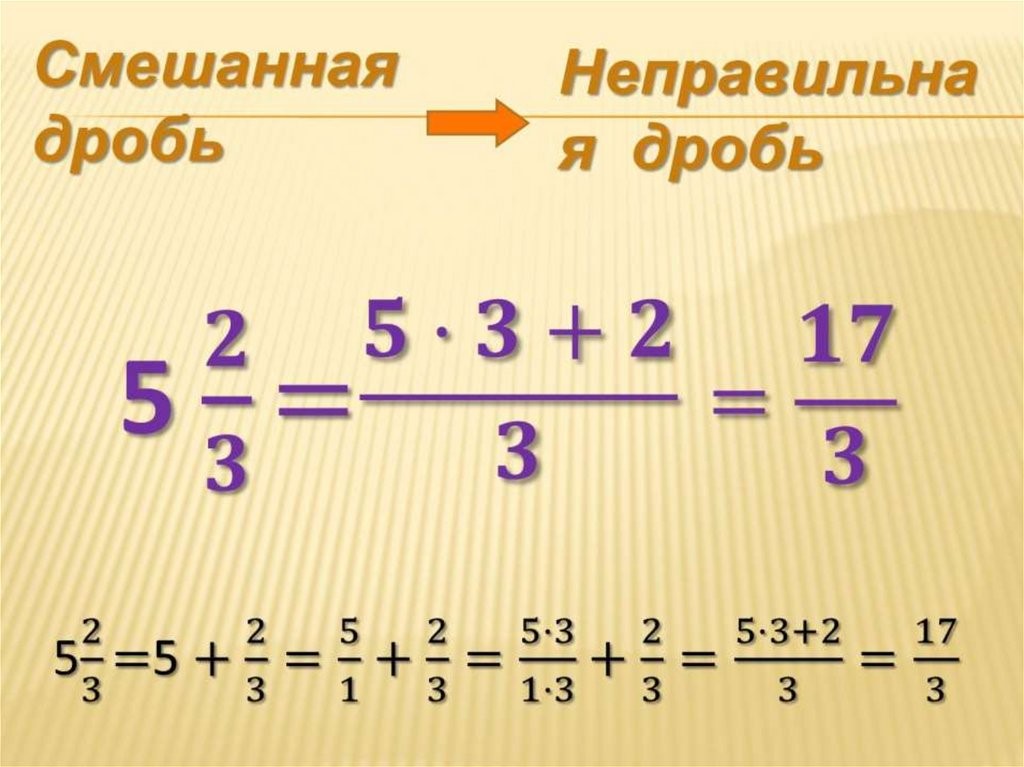
Смешанная дробь состоит из двух частей: целого и дробного чисел.

Но и такой вид дроби подлежит сокращению. Для объяснения этого действия необходимо превратить смешанную дробь в неправильную:

Источник: cf3.ppt-online.org

В приведенном примере конечная неправильная дробь не подлежит сокращению, поскольку числитель и знаменатель не имеют общего делителя.

Однако таким свойством обладают не все смешанные дроби.

Например,

\(54/8=44/8=11*4/2*4 =11/2\)

Из примера видно, что смешанная дробь превращена в неправильную и сокращена путем деления на наименьший общий делитель 4. При этом получен несократимый вариант, который можно обратно превратить в смешанную (или десятичную) дробь:

\(11/2=5,5 \)

Примеры решения задач

Решение: НОД дроби \(5/15 \) является 3. Разделив на 3 числитель и знаменатель, получаем \(1/5\)

Первым шагом превратим смешанную дробь в неправильную: \(56/8=46/8=(2*23)/(2*4)=23/4=53/4\)

Решение: \((43*2)/(21*2)=43/21\)

Решение: \(6/9+12/36=(2*3)/(3*3)+(1*12)/(3*12)=2/3+1/3=3/3\)

Результат примеры — неправильная дробь, в которой числитель равен знаменателю. Следовательно, ответом является 1.