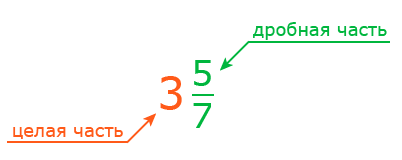Как решать смешанные дроби

Смешанные дроби — это

Источник: izamorfix.ru

Действия со смешанными дробями

Как преобразовать неправильную дробь в смешанную:

1. Шаг 1: Разделите числитель дроби на знаменатель, т.е. 15/7.
2. Шаг 2: Целая часть ответа будет целой частью смешанной дроби, то есть 2 — это целое число.
3. Шаг 3: Знаменатель будет таким же, как и в оригинале, то есть 7.
4. Шаг 4: Таким образом, неправильная дробь 15/7 превращается в смешанную дробь 2 (1/7).

Преобразование смешанной дроби в неправильную дробь:

1. Шаг 1: Умножьте знаменатель на целое число, т.е. в приведенном примере умножьте 7 на 2, 2(1/7).
   7 × 2 =14.
2. Шаг 2. К результату шага 1 прибавьте числитель дроби, т. е. прибавьте 1 + 14 = 15.
3. Шаг 3: Сохраните знаменатель прежним, то есть 7.
4. Шаг 4: Неправильная дробь получилась: 15/7.

Вычисления

Сложение смешанных дробей

Когда нужно сложить смешанные или неправильные дроби, знаменатели у обеих складываемых дробей могут быть как одинаковыми, так и разными.

Вот пошаговый метод сложения неправильных дробей с одинаковыми или разными знаменателями.

1. Шаг 1: Преобразуйте смешанные дроби в неправильные.
2. Шаг 2: Проверьте, одинаковы ли знаменатели.
3. Шаг 3: Если да, сложите числители дробей и запишите результат.
4. Шаг 4: Если знаменатели не одинаковые, то преобразуйте их в подобные дроби, найдите наименьшее общее кратное (НОК) знаменателей, чтобы они стали одинаковыми.
5. Шаг 5: Теперь сложите числители, чтобы получить результат сложения.

Решение:

После преобразования дробей в неправильные дроби получаем 3/2 и 5/2. При сложении 3/2 и 5/2 получаем 8/2. Упростив 8/2, получаем 4.

Умножение смешанных дробей

Чтобы умножить смешанные дроби, выполните следующие действия:

1. Шаг 1: Преобразуйте смешанные дроби в неправильные.
2. Шаг 2: Умножьте числитель на числитель и знаменатель и запишите результат.
3. Шаг 3: Результат можно упростить до наименьшей формы, оставить в виде неправильной или преобразовать в форму смешанной дроби.

Решение:

После преобразования дробей в неправильные дроби получаем 12/5 и 16/5. При умножении 12/5 и 16/5 получаем 192/25. Преобразуя 192/25 в смешанную дробь, получаем 7 (17/25).

Вычитание смешанных дробей

Чтобы вычесть смешанные дроби, выполните следующие действия:

1. Шаг 1: Преобразуйте смешанные дроби в неправильные.
2. Шаг 2: Проверьте, одинаковые ли у них знаменатели или нет.
3. Шаг 3: Если да, вычтите числители дробей и запишите результат.
4. Шаг 4: Если знаменатели не одинаковые, найдите НОК знаменателей, чтобы они стали одинаковыми.
5. Шаг 5: Теперь вычтите числители, чтобы получить результат вычитания.

Решение:

После преобразования дробей в неправильные дроби получаем 11/3 и 7/3. При вычитании 11/3 и 7/3 получаем 4/3. Преобразуя 4/3 в смешанную дробь, получаем  1 (1/3).

Деление смешанных дробей

Чтобы разделить смешанные дроби, выполните следующие действия:

1. Шаг 1: Преобразуйте смешанные дроби в неправильные.
2. Шаг 2: Умножьте первую дробь на обратное число второй дроби.
3. Шаг 3: Полученный результат можно упростить до наименьшей формы или оставить в виде неправильной или смешанной дроби.

Решение:

После преобразования дробей в неправильные дроби получаем 6/5 и 19/5. При делении 6/5 и 19/5 получаем (6/5) × (5/19), что равно 6/19.

Решение примеров со смешанными дробями

Решение:
5 вписывается в 23 целых 4 раза, поэтому целое число равно 4.
Остаток равен 3, поэтому в дробной части смешанного числа новый числитель равен 3 (знаменатель остается тем же, что и в исходной неправильной дроби). Поэтому ответ — 4⅗.

Ответ: 35 x 1½ = 52,5, ½ от 20 = 10, 52,5 + 10 = 62,5.

Решение:

Преобразуем смешанные дроби в неправильные. Получаем 5/3 и 10/3.
Поскольку знаменатели одинаковые, складываем числители. 5/3 + 10/3 = 15/3.
Упрощаем дробь, получаем 5.

Ответ = 5⁄2 + 8⁄5 = 25⁄10 + 16⁄10 = 41⁄10 = 4 и 1⁄10.

Решение:

К сложению или вычитанию, подобным этим, можно подойти одним из двух способов:

Сначала разделите смешанные числа на целые и правильные дроби, вычислите, а затем объедините, как в примере 1 выше: 1 + 1 = 2, ¼ + ½ = ¾, тогда 2 + ¾ = 2¾.
Сначала преобразуйте смешанные числа в неправильные дроби, вычислите их и при необходимости преобразуйте обратно в смешанные числа, как в примере 2 выше: 2⅓ - 1⅖ = 7⁄3 - 7⁄5 = 35⁄15 - 21⁄15 = 14⁄15.

 Решение:

Умножим знаменатель на целое число. Здесь 3 × 4 = 12
Добавим числитель к произведению, полученному на шаге 1. Здесь 12 + 1 = 13.
Запишем неправильную дробь, в которой сумма, полученная на шаге 2, является числителем, а знаменатель остается прежним. Это дает нам 13/3.

Решение:

К этой задаче можно подойти одним из двух способов:

1. Сначала разделите смешанное число на целую и правильную дробь, вычислите, а затем объедините: 1 x 5 = 5, ⅓ x 5 = 1⅔, 5 + 1⅔ = 6⅔.
2. Сначала преобразуйте смешанное число в неправильную дробь, вычислите, а затем при необходимости преобразуйте обратно в смешанное число: 1⅓ = 4⁄3, 4⁄3 x 5 = 20⁄3 = 6⅔.

Решение:

a.) Чтобы преобразовать неправильную дробь 16/5 в смешанную дробь, выполним следующие действия.

Разделим числитель на знаменатель. Здесь 16 ÷ 5.

Затем найдем делитель и остаток. Здесь делитель равен 3, а остаток - 1.
Расположим числа следующим образом: запишем делитель как целое число, за которым следует дробь остаток/делитель. Таким образом, смешанная дробь будет иметь вид
3 (1/5).

b.) Преобразовать неправильную дробь 17/7 в смешанную дробь.

17 ÷ 7
Найдем делитель и остаток. Здесь делитель равен 2, а остаток — 3.
Смешанная дробь будет выглядеть так: 2 (3/7).

Ответ: 24 х 58⅔ = 1408 часов.