Как вычислить смешанное произведение трех векторов
Свойства смешанного произведения векторов
На уроках в школе при решении физических, геометрических и математических задач часто приходится иметь дело с векторными величинами. Их отличие от обычных чисел заключается в наличии указания на некоторое направление. К примеру, таким образом, указывают, как направлена сила, приложенная к телу, каким способом ориентирован тот или иной луч, расположен объект по отношению к заданной точке.
В процессе работы с векторными величинами можно использовать ряд правил и закономерностей. Например, с их помощью значительно упрощаются действия сложения, вычитания, умножения величин. Нередко школьникам и студентам встречаются такие примеры, где требуется вычислить смешанное произведение векторов. Запишем свойства, которые характеризуют это действие:
- Три вектора являются компланарными тогда, когда каждый из них обладает значением, не равным нулю, а смешанное произведение данных векторов имеет нулевое значение, то есть: \(\left(\bar{a},\; \bar{b},\; c\right)=\left(\bar{b},\; \bar{a},\; \bar{c}\right)-\left(\bar{c},\; \bar{a},\; \bar{b}\right)\)
- Для смешанного произведения векторов справедливо следующее равенство: \(\left(\bar{a},\; \left[\bar{b},\; \bar{c}\right]\, \right)=\left(\bar{c},\; \left[\bar{a},\; \bar{b}\right]\, \right)=-\left(\bar{a},\; \left[\bar{c},\; \bar{b}\right]\, \right)=-\left(\bar{b},\; \left[\bar{a},\; \bar{c}\right]\, \right)=-\left(\bar{c},\; \left[\bar{b},\; \bar{a}\right]\, \right)\)
- Тождественное соотношение Якоби: \( \left(\bar{a},\; \left[\bar{b},\; \bar{c}\right]\, \right)+\left(\bar{b},\; \left[\bar{c},\; \bar{a}\right]\, \right)+\left(\bar{c},\; \left[\bar{a},\; \bar{b}\right]\, \right)=0\)
Как найти смешанное произведение векторов: формулы
Прежде чем приступить к записи уравнения для расчета искомого значения при действиях с векторами, следует ввести понятие смешанного произведения. С обозначением данного термина необходимо ознакомиться для понимания принципа математических действий, что поможет корректно выполнять расчеты к задачам различной степени сложности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Смешанным произведением \(\left(\bar{a},\; \bar{b},\; \bar{c}\right)\) трех векторов \(\bar{a},\; \bar{b} и \bar{c}\) является численное значение, которое определяется в виде результата скалярного произведению вектора \(\bar{a} \) на векторное произведение векторов \(\bar{b}\) и \(\bar{c}\): \(\left(\bar{a},\; \bar{b},\; \bar{c}\right)=\left(\bar{a},\; \left[\bar{b},\; \bar{c}\right]\right)\)
Как правило, в условиях задач по рассматриваемой теме указаны некоторые обозначения векторов, позволяющих идентифицировать их в трехмерном пространстве. Эта информация записана в координатной форме, то есть соответствует некоторым точкам на числовых осях, ориентированных в разных направлениях. Запишем еще одно выражение, исходя из полученных данных.
Будем считать, что для векторов \(\bar{a},\; \bar{b} и \bar{c}\) предусмотрены следующие координаты в пространстве:
\(\bar{a}=\left(a_{1} ;\; a_{2} ;\; a_{3} \right)\)
\(\bar{b}=\left(b_{1} ;\; b_{2} ;\; b_{3} \right)\)
\(\bar{c}=\left(c_{1} ;\; c_{2} ;\; c_{3} \right)\)
В результате можно записать соответствующую матрицу. При этом смешанное произведение рассматриваемых векторных величин будет вычисляться как матричный определитель. Сформулируем справедливое соотношение на основании логических заключений и доказательств:
\(\left(\bar{a},\; \bar{b},\; \bar{c}\right)=\left|\begin{array}{ccc} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \end{array}\right|\)
Геометрический смысл смешанного произведения векторов
Существуют математические понятия и категории, которые целесообразно рассмотреть также с точки зрения геометрии. В этом случае принято переводить числовые величины в значения некоторых элементом геометрических фигур. Далее, руководствуясь соответствующими закономерностями, теориями, правилами, свойствами, признаками таких фигур из геометрии, можно доказать справедливость математических соотношений, а также представить их логическое обоснование, сформулированное на основе наглядных примеров.
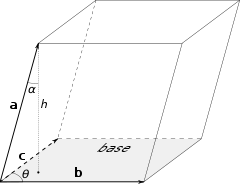
В случае смешанного произведения векторов разумно обратиться к геометрической фигуре в виде параллелепипеда. Представим, что такая фигура имеется. Изобразим ее в пространстве, начиная построения с некой точки, совпадающей с началом координат. При этом предположим, что имеет место равенство трех сторон этой фигуры некоторым вектором, которые обладают направлением и числовыми значениями, определяющими их протяженность. Перенесем исходные данные на рисунок:
Источник: ru.wikipedia.org
В результате, абсолютная величина смешанного произведения рассматриваемых векторов \(\mathbf {a}, \mathbf {b}, \mathbf {c}\) вычисляется как объему, который имеет изображенный на рисунке параллелепипед. Напомним, что данная геометрическая фигура составлена с помощью векторов \(\mathbf {a}, \mathbf {b} и \mathbf {c}\). Заметим, что расположение рассматриваемых векторов определяет тот факт, является ли окончательный результат положительным или отрицательным. Таким образом, в процессе расчетов требуется учитывать с правой или левой стороны отмечены данные по условию задания вектора.
Примеры решения задач
Дано три вектора с определенными координатами, обозначенные следующим образом:
\(\bar{a}=\left(1;\; 2;\; 3\right)\)
\(\bar{b}=\left(1;\; 1;\; 1\right)\)
\(\bar{c}=\left(1;\; 2;\; 1\right)\)
Необходимо выяснить, чему равно смешанное произведение записанных векторов.
Решение
Вспомним определение рассматриваемого в задаче понятия. Для того чтобы выполнить соответствующие действия с векторами, необходимо составить матрицу. В результате по значению определителя получится вычислить смешанное произведение. Определив порядок действий, выполним вычисления:
\(\left(\bar{a},\; \bar{b},\; \bar{c}\right)=\left|\begin{array}{ccc} 1 & 2 & 3 \\ 1 & 1 & 1 \\ 1 & 2 & 1 \end{array}\right|=1\cdot 1\cdot 1+1\cdot 2\cdot 3+2\cdot 1\cdot 1-1\cdot 1\cdot 3-2\cdot 1\cdot 1-1\cdot 2\cdot 1=2\)
Ответ: \(\left(\bar{a},\; \bar{b},\; \bar{c}\right)=2\)
Дана некая пирамида. Такая фигура изображена с помощью нескольких векторов:
\(\bar{a}=\left(1;\; 0;\; 1\right)\)
\(\bar{b}=\left(-1;\; 2;\; 3\right)\)
\(\bar{c}=\left(0;\; 1;\; -2\right)\)
Вычислим, чему равен объем заданной геометрической фигуры.
Решение
В данном случае целесообразно воспользоваться геометрической интерпретацией понятия смешанного произведения векторов. Заметим, что объем геометрической фигуры, которая образована рассматриваемыми векторами, составляет 1/6 от смешанного произведения этих векторов, взятого по модулю. Запишем соответствующее соотношение для проведения расчетов:
\(V_{pyr} =\frac{1}{6} \left|\left(\bar{a},\; \bar{b},\; \bar{c}\right)\right|\)
Заметим, что в условии задания указаны координаты для обозначенных векторов. Тогда для вычисления искомого произведения потребуется составить соответствующую матрицу и выявить ее определитель. Сформулируем определенные действия:
\(\left(\bar{a},\; \bar{b},\; \bar{c}\right)=\left|\begin{array}{ccc} 1 & 0 & 1 \\ -1 & 2 & 3 \\ 0 & 1 & -2 \end{array}\right|=1\cdot 2\cdot \left(-2\right)+\left(-1\right)\cdot 1\cdot 1+0\cdot 3\cdot 0-0\cdot 2\cdot 1-1\cdot 3\cdot 1-\left(-1\right)\cdot 0\cdot \left(-2\right)=-8\)
В результате, объем геометрической фигуры, который требуется найти по условию задачи, равен:
\(V_{pyr} =\frac{1}{6} \cdot \left|-8\right|=\frac{8}{6} =\frac{4}{3}\)
Ответ: \(\frac{4}{3}\)
Имеется некий параллелепипед. Представим, что в построении данной геометрической фигуры были использованы вектора: \(\vec{a},\vec{b},\vec{c}\) При этом результатом вычисления объема рассматриваемого параллелепипеда является V. Необходимо вычислить, чему равен объем параллелепипеда, который образован следующими векторами: \(\vec{p}=\vec{a}+\vec{b}+\vec{c},\qquad \vec{q}=\vec{a}+\vec{b}-\vec{c},\qquad \vec{r}=\vec{a}-\vec{b}+\vec{c}\,\)
Решение
В данном случае полезно вспомнить свойства для смешанного произведения векторов, а также смысл этого понятия, сформулированный с точки зрения геометрии. В первую очередь рассчитаем, чему равно смешанное произведение:
\(\begin{aligned} (\vec{p},\vec{q},\vec{r})=\,&(\vec{a}+\vec{b}+\vec{c},\vec{a}+\vec{b}-\vec{c},\vec{a}-\vec{b}+\vec{c})=\\[3pt] =\,&(\vec{a},\vec{a}+\vec{b}-\vec{c},\vec{a}-\vec{b}+\vec{c})+(\vec{b},\vec{a}+\vec{b}-\vec{c},\vec{a}-\vec{b}+\vec{c})+(\vec{c},\vec{a}+\vec{b}-\vec{c},\vec{a}-\vec{b}+\vec{c})=\\[3pt] =\,&\underbrace{(\vec{a},\vec{a},\vec{a}-\vec{b}+\vec{c})}_0+(\vec{a},\vec{b},\vec{a}-\vec{b}+\vec{c})-(\vec{a},\vec{c},\vec{a}-\vec{b}+\vec{c})+\\[3pt] \phantom{=\,}&+(\vec{b},\vec{a},\vec{a}-\vec{b}+\vec{c})+\underbrace{(\vec{b},\vec{b},\vec{a}-\vec{b}+\vec{c})}_0-(\vec{b},\vec{c},\vec{a}-\vec{b}+\vec{c})+\\[3pt] \phantom{=\,}&+(\vec{c},\vec{a},\vec{a}-\vec{b}+\vec{c})+(\vec{c},\vec{b},\vec{a}-\vec{b}+\vec{c})-\underbrace{(\vec{c},\vec{c},\vec{a}-\vec{b}+\vec{c})}_0=\\[3pt] =\,&\underbrace{(\vec{a},\vec{b},\vec{a})}_0-\underbrace{(\vec{a},\vec{b},\vec{b})}_0+(\vec{a},\vec{b},\vec{c})-\underbrace{(\vec{a},\vec{b},\vec{a})}_0+(\vec{a},\vec{c},\vec{b})-\underbrace{(\vec{a},\vec{c},\vec{c})}_0+\\[3pt] \phantom{=<br />,}&+\underbrace{(\vec{b},\vec{a},\vec{a})}_0-\underbrace{(\vec{b},\vec{a},b)}_0+(\vec{b},\vec{a},\vec{c})-(\vec{b},\vec{c},\vec{a})+\underbrace{(\vec{b},\vec{c},\vec{b})}_0-\underbrace{(\vec{b},\vec{c},\vec{c})}_0+\\[3pt] \phantom{=\,}&+\underbrace{(\vec{c},\vec{a},\vec{a})}_0-(\vec{c},\vec{a},\vec{b})+\underbrace{(\vec{c},\vec{a},\vec{c})}_0-(\vec{c},\vec{b},\vec{a})+\underbrace{(\vec{c},\vec{b},\vec{b})}_0-\underbrace{(\vec{c},\vec{b},\vec{c})}_0=\\[3pt] =\,&(\vec{a},\vec{b},\vec{c})+\underbrace{(\vec{a},\vec{c},\vec{b})}_{-(\vec{a},\vec{b},c)}+\underbrace{(\vec{b},\vec{a},\vec{c})}_{-(\vec{a},\vec{b},c)}-\underbrace{(\vec{b},\vec{c},a)}_{(\vec{a},\vec{b},c)}-\underbrace{(\vec{c},\vec{a},\vec{b})}_{(\vec{a},\vec{b},c)}+\underbrace{(\vec{c},\vec{b},\vec{a})}_{-(\vec{a},\vec{b},c)}=-4\cdot(\vec{a},\vec{b},\vec{c}), \end{aligned}\)
Далее целесообразно выразить модуль полученного значения:
\(|(\vec{p},\vec{q},\vec{r})|=|-4|{\cdot}|(\vec{a},\vec{b},\vec{c})|=4V\)
Исходя из геометрического смысла смешанного произведения векторов, получим, что объем геометрической фигуры, параметры которой приведены в условии задания, составляет 4V.
Ответ: 4V
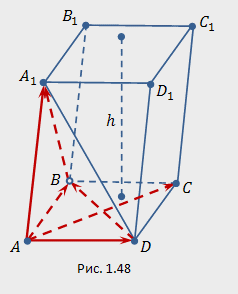
На плоскости задана некая геометрическая фигура, которая имеет вид параллелепипеда. Предположим, что ее обозначение соответствует \(ABCDA_1B_1C_1D_1\), а в построении участвуют следующие вектора: \(\overrightarrow{AB}=\vec{i}+2\vec{j}+2\vec{k}, \overrightarrow{AD}=3\vec{i}-2\vec{j}+\vec{k}, \overrightarrow{AA_1}=2\vec{i}-\vec{j}+3\vec{k}\)
Источник: mathhelpplanet.com
Нужно выполнить соответствующие вычисления и представить ответы на несколько вопросов:
- смешанное произведение \(\bigl(\overrightarrow{AB}, \overrightarrow{AD}, \overrightarrow{AA_1}\bigr)\) и расположение \(\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AA_1}\) ;
- объем, который имеет треугольная пирамида \(ABDA_1\);
- высоту h параллелепипеда, то есть удаленность плоскостей, в которых расположены основания \(ABCD и A_1B_1C_1D_1\).
Решение
Найдем ответ на первый вопрос, то есть вычислим, чему равно смешанное произведение векторов, ориентируясь на геометрический смысл данного понятия. Запишем подходящую формулу и подставим численные значения из условия задачи:
\(\bigl(\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AA_1}\bigr)=\begin{vmatrix}1&2&2\\3&-2&1\\2&-1&3\end{vmatrix}=-17\)
Заметим, что в результате имеется знак минуса. Исходя из этого, целесообразно сделать вывод о том, что рассматриваемые вектора расположены слева.
Так как даны координаты для векторов, можно вычислить с помощью определителя матрицы значение смешанного произведения этих векторов:
\(\vec{a}=\overrightarrow{AB}, \vec{c}=\overrightarrow{AA_1}, \vec{a}=\overrightarrow{AB}\)
\(a=\begin{pmatrix}1\\2\\2\end{pmatrix}\!,\qquad b=\begin{pmatrix}3\\-2\\1\end{pmatrix}\!,\qquad c=\begin{pmatrix}2\\-1\\3\end{pmatrix}\)
\(\bigl(\vec{a},\vec{b},\vec{c}\bigr)=\begin{pmatrix}1&2&2\end{pmatrix}\!\cdot\!\begin{pmatrix}0&-1&-2\\1&0&-3\\2&3&0\end{pmatrix}\!\cdot\!\begin{pmatrix}2\\-1\\3\end{pmatrix}=\begin{pmatrix}1&2&2\end{pmatrix}\!\cdot\!\begin{pmatrix}-5\\-7\\1\end{pmatrix}\)
Далее приступим к поиску объема пирамиды, вписанной в параллелограмм. Заметим, что эти геометрические фигуры имеют равные высоты. Кроме того, площадь основания пирамиды \(ABDA_1\) определяется как ½ площади основания параллелограмма ABCD. В таком случае, объем рассматриваемой треугольной пирамиды в 6 раз меньше объема данного по условию задания параллелепипеда.
\(V=\frac{h}{3}\cdot S_{\text{osn}}=\frac{1}{3}\cdot\frac{1}{2}\cdot S_{*}\cdot h=\frac{1}{6}\cdot V_{*}.\)
\(V_{*}=\Bigl|\bigl(\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AA_1}\bigr)\Bigl|\,=17\)
\(V=\frac{1}{6}\cdot V_{*}=\frac{17}{6}\)
На последнем шаге можно вычислить, чему равна высота параллелепипеда:
\(h=\frac{V_{*}}{S_{*}}\)
\(V_{*}=17\)
\(S_{*}=5\sqrt{5}\)
\(h=\frac{17}{5\sqrt{5}}\)
Ответ: -17, \(\frac{17}{6}, \frac{17}{5\sqrt{5}}\).
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так