Какие углы называются смежными
Смежные углы — это
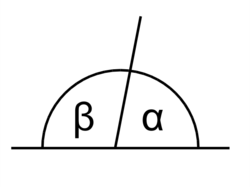
Смежными называют пару углов, у которых одна сторона является общей, а две другие взаимно дополняют друг друга до прямой линии.
Источник: ru.wikipedia.org
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Проанализируем изображение смежных углов. Заметим, что данные объекты обладают единой стороной в виде прямой линии. В результате сопоставления рассматриваемых углов получается развернутый угол. Из курса геометрии известно, что градусная мера развернутого угла составляет \(180^{\circ}\). Исходя из озвученного утверждения, можно заключить, что суммирование смежных углов дает величину в 180 градусов.
Источник: ru.wikipedia.org
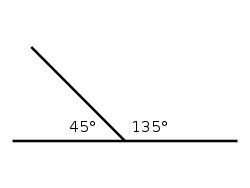
На следующем рисунке наглядно продемонстрирована сумма смежных углов, равная \(45^{\circ} + 135^{\circ} = 180^{\circ}\).
Признаки и свойства
Решая примеры по геометрии, важно правильно идентифицировать фигуру, чтобы применять в дальнейшем подходящие формулы и закономерности для проведения расчетов тех или иных величин углов, треугольников, многоугольников. Смежные углы обладают рядом характерных признаков, по которым их легко распознать:
- наличие единой вершины;
- присутствие общей стороны, находящейся между углами.
На следующем шаге поиска ответа к задачам на вычисление параметров смежных углов полезно использовать свойства, которыми обладают данные виды геометрических объектов. Перечислим основные правила и положения:
- В сумме смежные углы составляют \(180^{\circ}\). При необходимости в определении градусной меры одного из смежных углов нужно вычесть из \(180^{\circ}\) величину известного угла.
- Смежные углы являются дополнением друг друга. Когда имеется произвольная пара смежных углов, в сумме составляющих \(180^{\circ}\), такие объекты называют дополняющими углами. С помощью определения величины одного из них несложно в дальнейшем рассчитать градусную меру второго.
- Допустима ситуация, при которой углы являются смежными и вертикальными. Подобный случай возможен при образовании сторонами рассматриваемых углов прямой линии, перпендикулярной к общей стороне. Тогда градусные меры геометрических объектов равны и составляют \(90^{\circ}\) для каждого угла.
Какова сумма смежных углов
При суммировании смежных углов получается градусная величина, равная \(180^{\circ}\).
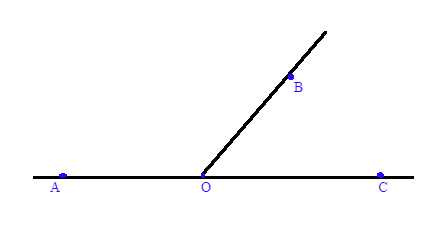
В доказательство сформулированной теоремы изобразим пару смежных углов. Обозначим их за \(\angle АОВ и \angle ВОС\).
Исследуем изображение выше. Заметим, что луч ОВ расположен в пространстве на плоскости, разделяющем стороны углов ОА и ОС, которые являются элементами развернутого угла. Из теоретического материала известно, что развернутый угол составляет \(180^{\circ}\). Исходя из озвученного утверждения, допустимо прийти к выводу о соответственном равенстве суммы углов \(\angle АОВ и \angle ВОС\) величине \(180^{\circ}\). Таким образом, смежные углы в сумме равны \(180^{\circ}\).
Задачи
Задан развернутый угол, обозначенный за АВС. С помощью луча ВD данный угол поделен на пару смежных углов АВD и DВС. В результате построения градусная мера угла АВD превышает величину DВС на \(40^{\circ}\). Необходимо найти, какой градусной мере соответствуют углы АВD и DВС.
Решение
Проанализируем условия задания. Исходя из озвученного соотношения градусных мер смежных углов, составим следующее равенство:
\(\angle АВD = \angle DВС + 40^{\circ}\)
По ранее изученной теории о смежных углах известно, что в сумме такие геометрические фигуры составляют \(180^{\circ}\). Запишем это утверждение в математическом виде, применительно к условиям задачи:
\(\angle АВD + \angle DВС = 180^{\circ}\)
Объединим два уравнения в одно справедливое равенство, выразив один смежный угол через величину второго угла:
\(\angle DВС + \angle DВС + 40^{\circ} = 180^{\circ}\)
Выполним некоторые преобразования в уравнении и рассчитаем градусную меру одного из смежных углов:
\(2\angle DВС + 40^{\circ} = 180^{\circ}\)
\(2\angle DВС = 140^{\circ}\)
\(\angle DВС = 70^{\circ}\)
В таком случае второй смежный угол несложно посчитать по стандартной формуле:
\(\angle АВD = 180^{\circ} - 70^{\circ} = 110^{\circ}\)
Ответ: \( \angle АВD = 110^{\circ}, \angle DВС = 70^{\circ}.\)
Имеется некий развернутый угол DCA. Из вершины этой геометрической фигуры провели луч СО. Угол \(\angle АСО равен 25^{\circ}\). Необходимо вычислить градусную меру угла \(\angle DСО\).
Решение
Если внимательно проанализировать условия задания, то можно заметить признаки смежных углов, которые в сумме составляют развернутый угол. Таким образом:
\(\angle DСО + \angle АСО = 180^{\circ}\)
Подставим известную величину в уравнение и запишем следующее соотношение:
\(\angle DСО + 25^{\circ} = 180^{\circ}\)
Вычислим один из смежных углов \(\angle DСО\):
\(\angle DСО = 180^{\circ} - 25^{\circ} = 155^{\circ}\)
Ответ: \(\angle DСО = 155^{\circ}.\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так