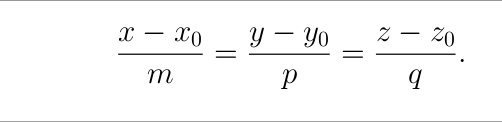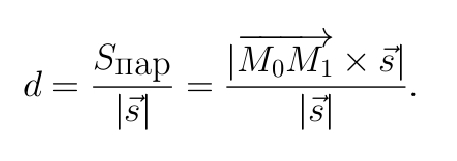Вычисление расстояние от точки до прямой по формуле

Определение расстояния от точки до прямой

Пусть прямая l в пространстве задана своими каноническими уравнениями:

Точка  \(M0 (x0, y0, z0) ∈ l\),  \(\vec{s} = (m, p, q)\) — направляющий вектор прямой l. Необходимо найти расстояние d от точки M₁ (x₁, y₁, z₁) до прямой l.

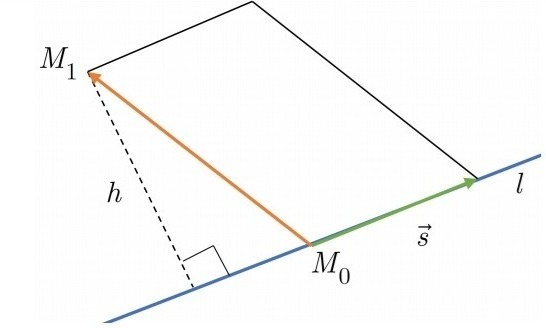
Построим параллелограмм на векторах \(\overrightarrow{М_{0}М_{1}}\) и \(\vec{s}\) . 

Тогда расстояние от точки M₁ до прямой l будет равно высоте h параллелограмма:

Способы определения расстояния

Очень интересный способ определения расстояния — графический.

 Конкретно — применение формулы расстояния между двумя точками прямоугольной декартовой системы координат XOY.

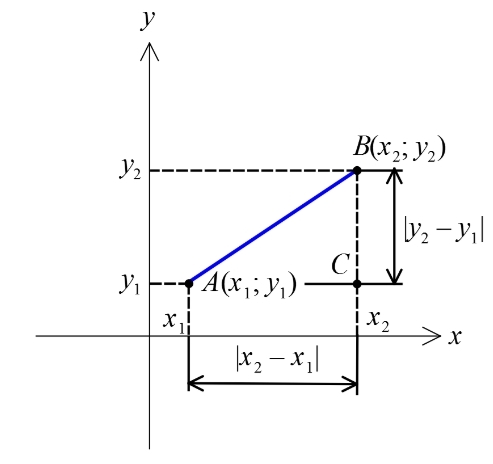
 Выводить эту формулу достаточно просто: пусть на плоскости XOY заданы две точки А(x₁; y₁) и B(x₂; y₂).

Нужно определить расстояние между этими точками. Другими словами — вычислить длину отрезка АВ. Как видно из рисунка, данный отрезок — гипотенуза прямоугольного треугольника АВС с катетами АС и ВС. Их длины равны разности абсцисс и ординат концов А и В отрезка АВ:

\(AC=|x_{2}-x_{1}| \)

\(BC=|y_{2}-y_{1}|\)

Модули ставят, чтобы было неважно, как именно ориентирован отрезок и какая из координат больше — первая или вторая: модуль просто отсекает возможный минус, если, вдруг,  х₂ окажется меньше, чем х₁. Ведь длина отрезка, очевидно, величина не отрицательная.

Применив теорему Пифагора, получим  искомое расстояние:

\(AB^{2}=AC^{2}+BC^{2}\)

\(AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{|x_{2}-x_{1}|+|y_{2}-y_{1}|}^{2}\). 

Поскольку как квадрат, так и модуль обладают одним свойством — четностью, то модули под корнем можно заменить на обычные скобки.

Еще один способ определения расстояния — аналитический

Аналитические способы основаны на тригонометрических зависимостях между углами и сторонами в плоском треугольнике, одной из сторон которого является искомое расстояние. При этом, вместо самого искомого расстояния непосредственно измеряются какие-то три других элемента в соответствующем треугольнике, например, одна из других сторон (более короткая и/или удобная для непосредственного измерения) и прилегающие к ней два угла треугольника, либо же две другие стороны треугольника и угол между ними. В первом случае искомое расстояние (неизвестная сторона треугольника) вычисляется по теореме синусов, а во втором — по теореме косинусов.

Формулы нахождения расстояния

На плоскости:

В пространстве:

Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве

Задача 

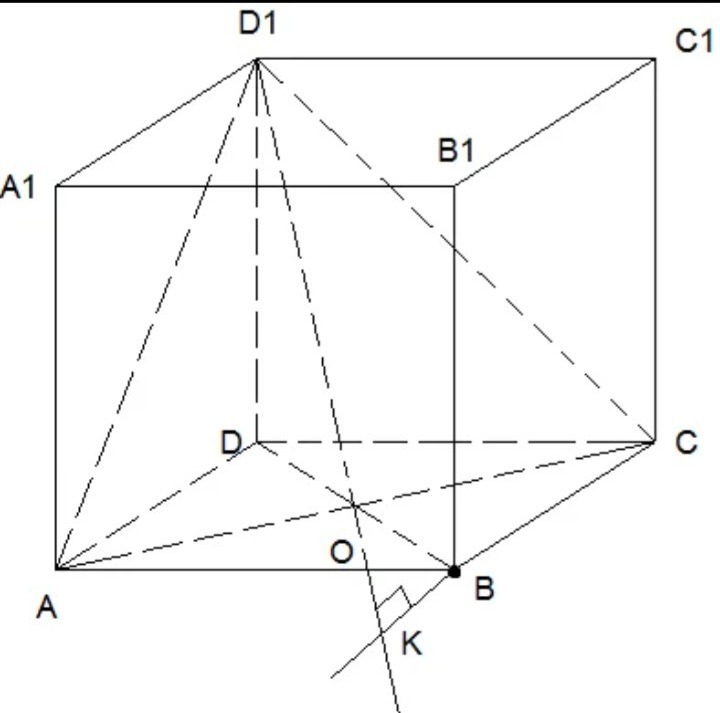
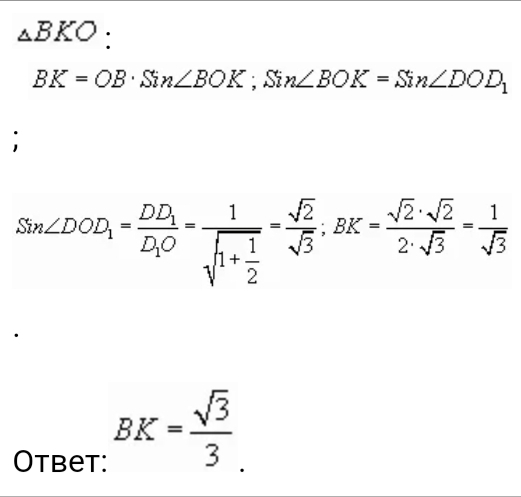
единичном кубе A....D1 найти расстояние от точки В до AD1C .

На данной плоскости ACD₁ выбираем прямую АС, перпендикулярно которой проводим две пересекающиеся прямые ВD и D₁O. Прямые BD, D₁O и точка B лежат в одной плоскости BB₁D. Плоскости ACD₁  и BB₁D перпендикулярны по признаку перпендикулярности плоскостей (AC ⊥ BB₁D). Из точки B опускаем перпендикуляр ВК на линию пересечения этих плоскостей — D₁O. ВК — искомое расстояние.