Формулы производной тангенса
Что такое тангенс
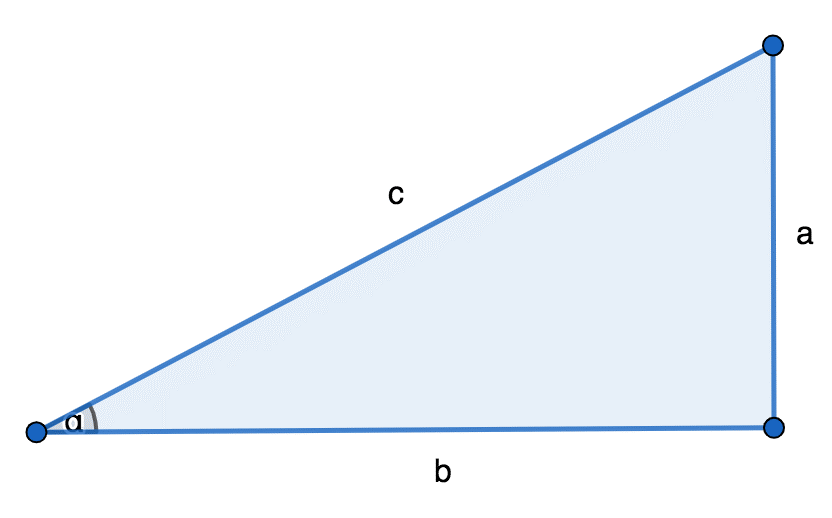
Тангенс некоторого угла \(\alpha\), который меньше девяносто градусов, представляет собой отношение противоположного катета а к прилегающему катету b в треугольной геометрической фигуре с прямым углом.
Источник: microexcel.ru
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Записанное определение целесообразно выразить с помощью формулы:
\(\tan\alpha = \frac{a}{b}\)
В качестве обозначения тангенса какого-либо угла используют выражения: tg или tan.
Представим, что известны длины отрезков в геометрической фигуре, изображенной схематично выше. Пусть величины этих сторон равны: а = 3 b = 4
Воспользуемся формулой для вычисления тангенса угла, подставим известные значения и выполним математические операции:
\(\tan\alpha = \frac{a}{b} = \frac{3}{4} = 0,75\)
Тогда получим, что:
\(\tan\alpha = 0,75\)
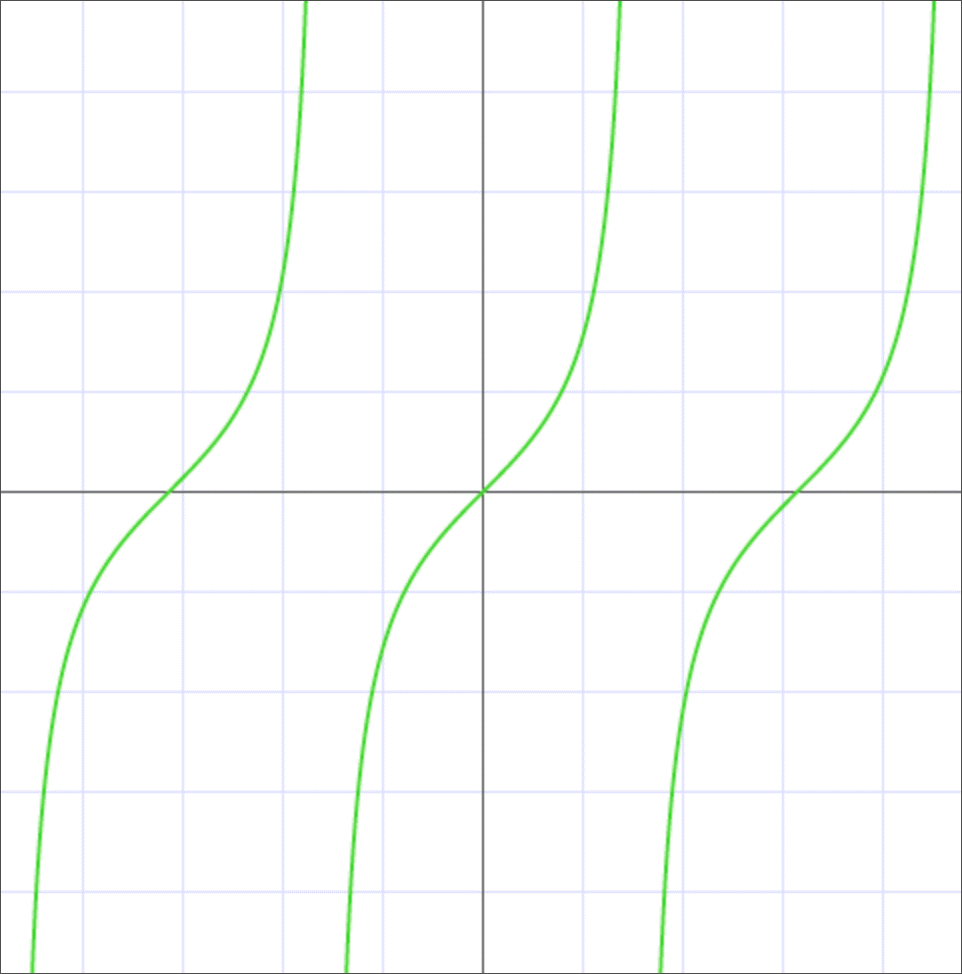
В процессе поисков ответов на примеры из тригонометрии обычно возникает необходимость в построении графиков функций. Поиск переменных графическим методом является одним из наиболее точных и эффективных способов. Представим на координатной плоскости тригонометрическую функцию y = tg (x).
Источник: microexcel.ru
Что такое производная tgx
Производная тригонометрической функции тангенс вычисляется как частное от деления единицы на косинус во второй степени аналогичного аргумента, то есть: \((tg x)' = \frac{1}{\cos^2 x}\)
Прийти к такому выводу можно путем поэтапного доказательства. В первую очередь целесообразно представить тангенс через синус и косинус. На этот случай имеется справедливое тригонометрическое тождество. Запишем соотношение:
\(tg x = \frac{\sin x}{\cos x}\)
Далее необходимо вычислить, чему равна производная от косинуса и синуса. Запишем выражения ниже:
\((\sin x)' = \cos x\)
\((\cos x)' = -\sin x\)
Известно, что для определения производной от дробного числа проще всего воспользоваться специальным правилом. Тогда расчеты значительно упрощаются. Найдем производную:
\( (tg x)' = \bigg (\frac{\sin x}{\cos x} \bigg )' = \frac{(\sin x)' \cdot \cos x - \sin x \cdot (\cos x)'}{\cos^2 x} = (tgx)\)
Упростим выражение, которое записано на месте числителя. При этом важно обратиться к справедливому равенству:
\(\sin^2 x + \cos^2 x = 1sin\)
Запишем порядок вычислений:
\(\frac{\cos x \cdot \cos x - \sin x \cdot (-\sin x)}{\cos^2 x} = \frac{\cos^2 x + \sin^2 x}{\cos^2 x} = \frac{1}{\cos^2 x}\)
Производная tgx 2
Производную тригонометрической функции тангенса допустимо возводить во вторую степень. Однако в этом случае нет необходимости выполнять громоздкие вычисления, перемножая сложные выражения между собой. Достаточно применить в расчетах более простую формулу.
На первом этапе запишем соотношение, подходящее для расчета производной тангенса некоторого угла, который является обратным для котангенса:
\(\tan ^{2}(x)\)
Если заменить тангенс переменной, получим:
\(u=\tan (x)\)
Затем , прибегая к составному правилу, запишем:
\(u ^{2}\) получим 2u
На следующем шаге целесообразно вычислить произведение:
\(\frac{d}{dx}\tan (x)\)
Найдем, чему соответствует производная:
\(\frac{d}{dx}\tan (x)=\frac{1}{\cos^2 (x)}\)
\(\frac{2 tan (x)}{\cos^2( x)} (\sin ^{2}(x)+\cos ^{2}(x))\)
Соотношение, которое получилось в итоге, стоит упростить:
\(\frac{2 tan (x)}{\cos^2( x)}\)
В результате, доказано равенство:
\(\tan ^{2}(x) = \frac{2 tan (x)}{\cos^2( x)}\)
Производная от тангенса в кубе
Аналогично путем поэтапных вычислений и математических преобразований можно найти значение производной от тригонометрической функции тангенса в третьей степени, то есть в кубе:
\(\tan ^{3}(x)\)
Определим, как рассчитать первую производную степени. С этой целью можно воспользоваться следующим выражением:
\((3\tan ^{2}(x)+3) \tan ^{2}(x)\)
Как и в предыдущем примере при вычислении производной квадрата тангенса, в данном случае целесообразно прибегнуть к замене:
\(u=\tan(x)\)
В результате, из \(u ^{3}\) получим \(3u^{2}\). Известно, что для поиска степени некоторого числа предусмотрена обратная операция, которая заключается в извлечении корня. Затем с помощью уже знакомых правил найдем произведение:
\(\frac{d}{dx}\tan (x)\)
При выполнении дифференцирования проще всего изменить вид записи функций:
\(\tan (x)=\frac{\sin (x)}{cos(x)}\)
Заметим, что здесь можно воспользоваться правилом производной от деления. Выполним необходимые преобразования:
\(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{-f(x)\frac{d}{dx}g(x)+g(x)\frac{d}{dx}f(x)}{g^{2}(x)}\)
Далее потребуется учитывать следующее условие:
\(f(x)= sin (x)\)
\(g(x)= cos(x)\)
Попробуем рассчитать, чему равно такое выражение:
\(\frac{d}{dx} f(x)\)
В процессе важно учитывать следующее справедливое равенство:
\(\frac{d}{dx} sin (x)= cos(x)\)
Вычислить значение выражения \(\frac{d}{dx} g(x)\) несложно, если знать об отрицательном значении синуса при определении производной косинуса:
\(\frac{d}{dx} cos(x) = -sin (x)\)
Затем целесообразно применить в процессе вычислений закономерность производной от частного:
\(\frac{\sin ^{2}(x)+\cos ^{2}(x)}{\cos^{2}(x)}\)
Путем применения в данной ситуации рассмотренных ранее правил выполним все нужные преобразования:
\(\frac{3(\sin ^{2}(x)+\cos ^{2}(x))\tan ^{2}(x)}{\cos^{2}(x)}\)
Полученное выражение несложно упростить. В итоге получим:
\(\frac{3\tan ^{2}(x)}{\cos^{2}(x)}\)
Запишем окончательную формулу:
\(\tan ^{3}(x)\)
Примеры решения задач
Дана сложная функция тангенса: \(y = tg 2x\) Требуется вычислить, чему равна производная от записанного выражения.
Решение
Из определения производной тангенса известно, что при вычислении искомого значения требуется разделить единицу на косинус во второй степени от аналогичного аргумента. Заметим, по условию задачи дана сложная функция. По этой причине на втором этапе дополнительно умножим значение на производную аргумента тангенса. С учетом всех преобразований получим:
\(y' = (tg 2x)' = \frac{1}{\cos 2x} \cdot (2x)' = \frac{1}{\cos 2x} \cdot 2 = \frac{2}{\cos 2x}\)
Ответ: \(y' = \frac{2}{\cos 2x}\).
Требуется вычислить значение производной от тригонометрической функции тангенса во второй степени: \(y = tg^2 x\)
Решение
В этом случае целесообразно воспользоваться следующей справедливой закономерностью:
\((x^p)' = px^{p-1}\)
Далее можно найти произведение:
\(y' = (tg^2 x)' = 2tg x \cdot (tg x)' = 2tg x \cdot \frac{1}{\cos^2 x} = 2\frac{tg x}{\cos^2 x} = 2 \frac{\sin x}{\cos^3 x}\)
Ответ: \(y' = 2\frac{\sin x}{\cos^3 x}\).
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так