Способы сложения векторов
Что такое вектор
В науке геометрии нередко встречается понятие вектора. Под этим распространенным термином понимают некоторый отрезок в плоскости с определенными граничными точками. Одна отметка играет роль начала, а вторая представляет собой конец проведенной линии. В информационных источниках вектором также называют какой-либо направленный отрезок.
Вектор представляет собой отрезок с направлением, который соединяет пару точек, принятых за его начало и конец.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: ru.wikipedia.org
В типичных геометрических задачах с целью обозначения вектора используют две заглавные буквы алфавита или одну строчную букву. Над символом изображают стрелку или прямую линию. Например, на рисунке выше представлен вектор \( \overrightarrow {АВ}\). Не допускается перестановка букв в наименовании направленного отрезка. На схеме А является началом, а В представляет собой конечную точку вектора.
В процессе определения векторных координат рассчитывают разность между координатами, которым соответствуют начальная и конечная отметка рассматриваемого вектора. Предположим, что известны координаты некоторого вектора:
\(T_{1}=(x_{1},y_{1})\)
\(T_{2}=(x_{2},y_{2})\)
При исходных данных несложно посчитать векторные координаты:
\(\overrightarrow {V}=T_{2}-T_{1}=(x_{2},y_{2})-(x_{1},y_{1})=(x_{2}-x_{1},y_{2}-y_{1})\)
Другая полезная характеристика векторных величин является длиной. Под этим термином подразумевают расстояние, на которое удалены точки вектора \(\overrightarrow {V}\), обозначенные за \(T_{1} и T_{2}\) соответственно. При обозначении длины применяют следующее соотношение:
\(|{\overrightarrow {V}}|=|T_{2}-T_{1}|=|(x_{2}-x_{1},y_{2}-y_{1})|={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\)
Законы сложения векторов
В разных научных областях, включая физику и геометрию, с векторными величинами производят математические операции. К одной из подобных процедур относят суммирование векторов. Такие действия несложно выполнить при наличии знаний определенных свойств и закономерностей. В первую очередь целесообразно ознакомиться с ключевыми понятиями этой темы.
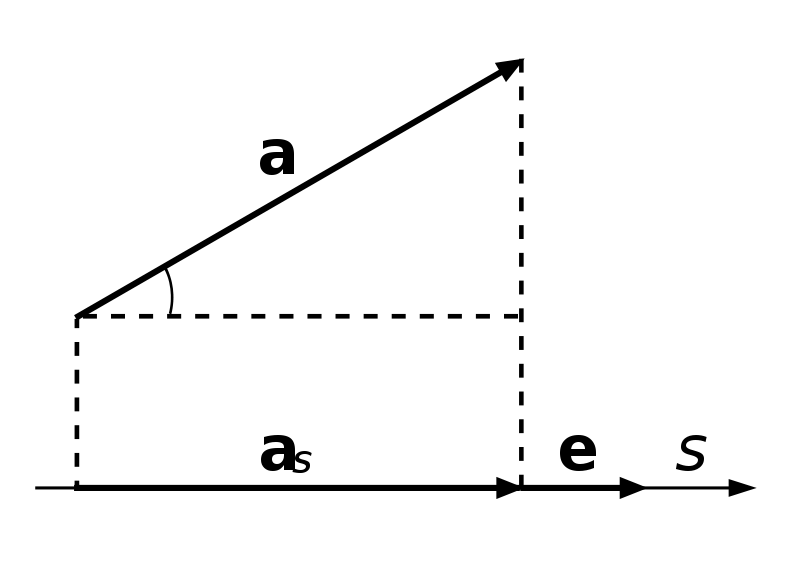
Векторы представляют в системе координат, используя проекцию на ось. Данным понятием обозначают протяженность отрезка, который сформирован с помощью проекций начальной и конечной точки на выбранную прямую линию. Когда направленность вектора и оси совпадают, проекцию считают положительной. При условии разных направлений векторного отрезка и оси добавляют знак минуса к проекции. Проекцию вычисляют как произведение длины начального вектора и косинуса угла, расположенного между векторным отрезком и осью. Проекция вектора, построенная перпендикулярно относительно оси, имеет нулевой значение.
Источник: ru.wikipedia.org
Векторы применяют для обозначения направлений каких-либо величин, к примеру, воздействующей на предмет силы, скорости, с которой перемещается тот или иной объект в заданном направлении. Использование векторных отрезков в этом смысле значительно упрощает проведение вычислений и исследований. С помощью характерных для них свойств рассчитывают градусную и радианную меру углов, соединяющих прямые линии и отрезки, определяют площадь геометрических фигур.
По правилу треугольника
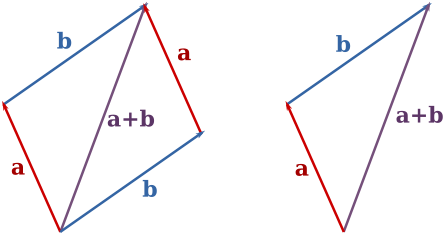
При наличии пары векторных отрезков в пространстве допустимо выполнить сложение величин по правилу треугольника. В процессе решения следует воспользоваться простым алгоритмом действий:
- отмерить начало первого вектора от конечной точки второго направленного отрезка;
- вектор суммы соответствует третьему вектору, соединяющему начальную отметку первого вектора и конечную точку второго вектора.
Источник: ru.wikipedia.org
По правилу параллелограмма
Следующий способ суммирования пары векторов заключается в применении правила параллелограмма. Реализовать описанную методику можно путем последовательного выполнения инструкции:
- совместить два вектора;
- построить второй векторный отрезок, начиная с конца первого вектора;
- отложить от конечной отметки второго вектора отрезок, равный первому вектору;
- в полученном параллелограмме провести диагональ, образующую искомый векторный отрезок в виде суммы исходных векторов.
Озвученный принцип сложения векторов имеет сходство с первым способом расчета суммы путем образования треугольника. Общий смысл теорем состоит в необходимости перемещения векторных отрезков в пределах плоскости для получения нужной геометрической фигуры. В случае отсутствия общих точек у заданных векторов применение перечисленных методов не представляется возможным.
По правилу многоугольника
Когда условия задачи подразумевают суммирование векторов в количестве большим, чем два, применяют методику многоугольника, которая представляет собой расширенную версию доказательства правила треугольника. Руководствуясь этим способом, в выбранной последовательности необходимо совместить конечные и начальные точки векторных отрезков.
В результате получается геометрическая фигура с множеством углов. Остается построить суммирующий вектор. Начало искомого отрезка совпадает с исходной точкой первого вектора, а конец результирующего отрезка находится в точке, аналогичной концу последнего векторного отрезка.
Формулы
В процессе решения задач на действия с векторами прибегают к декартовой координатной системе, что позволяет определить координаты рассматриваемых направленных отрезков путем разложения по базисным векторам. Подобный способ заключается в применении векторной проекции на оси координат. При известных координатах начальной и конечной отметки вектора его координаты вычисляют таким образом:
\(\overrightarrow {AB}=(AB_{x},AB_{y},AB_{z})=(B_{x}-A_{x},B_{y}-A_{y},B_{z}-A_{z})\)
За базис обычно принимают орты координат, то есть \({\vec {i}},{\vec {j}},{\vec {k}}\), соответствующие осям x,y,z. В результате направленный отрезок \({\vec {a}}\) допустимо представить в следующем виде:
\({\vec {a}}=a_{x}{\vec {i}}+a_{y}{\vec {j}}+a_{z}{\vec {k}}\)
Удобство работы с векторами обеспечивает возможность записи какого-либо геометрического свойства в координатной плоскости. По итогам подобных преобразований можно перейти к алгебраическим вычислениям. Обратное утверждение справедливо лишь для тех положений, которые являются инвариантными, то есть реализуемыми в любой декартовой системе.
Другое полезное понятие, связанное со сложением и прочими операциями с направленными отрезками, распространяется на модуль вектора. Представим, что имеется векторная величина \( \overrightarrow {AB}\). Тогда модулем является численное значение, определяемое как протяженность отрезка АВ. С целью обозначения модуля используют \(|\overrightarrow {AB}|.\)
Примеры решения задач
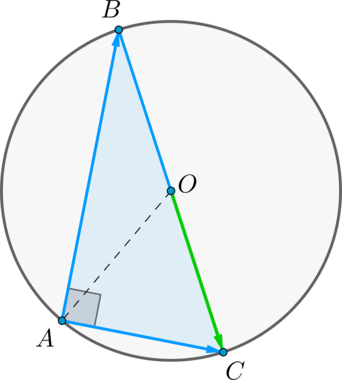
Изображена треугольная геометрическая фигура с прямым углом АВС. Угол А равен 90°. Точка О является центральной отметкой для окружности, которая описана около заданного треугольника. Требуется вычислить сумму координат вектора \(\overrightarrow {ОС}\) при следующих условиях:
\(\overrightarrow {AB} = {1; 1}\)
\(\overrightarrow {AС} = {-1; 1}\)
Источник: shkolkovo.net
Решение
Ознакомимся с изображением из условия задания. Из курса геометрии известно, что в прямоугольном треугольнике центр описанной окружности совпадает со средней частью гипотенузы. Таким образом, отметка О делит пополам ВС. Согласно закономерности заданной геометрической фигуры, допустимо составить следующее равенство:
\(\overrightarrow {BС} = \overrightarrow {AС} - \overrightarrow {AB}\)
Вычислить координаты вектора \(\overrightarrow {BС}\) можно с помощью уравнения:
\(\overrightarrow {BС} = {-1 - 1; 1 - 1} = {-2; 0}\)
Ранее определили, что ОС составляет половину от отрезка ВС. Используя эту информацию, следует вычислить координаты вектора \(\overrightarrow {ОС}\):
\(\overrightarrow {ОС} = \frac{1}{2} \overrightarrow {BС}\)
\(\overrightarrow {ОС} = {-1; 0}\)
На последнем этапе вычислений найдем, чему равна искомая сумма координат вектора \(\overrightarrow {ОС}\):
-1 + 0 = -1
Ответ: -1.
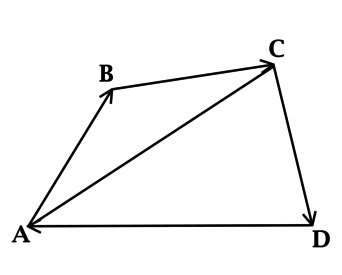
Задана четырехугольная геометрическая фигура АВСD. Стороны данного объекта соответствуют векторам \(\overrightarrow {АB}, \overrightarrow {BС}, \overrightarrow {СD}, \overrightarrow {DА}\). Нужно вычислить значение длины направленного отрезка, состоящего из суммы перечисленных векторов.
Источник: shkolkovo.net
Решение
На первом этапе решения задачи обратимся к изображению четырехугольника и запишем несколько полезных для дальнейших вычислений соотношений:
\(\overrightarrow {АВ} + \overrightarrow {ВС} = \overrightarrow {АС}\)
\(\overrightarrow {АС} + \overrightarrow {СD} = \overrightarrow {AD}\)
Исходя из приведенных равенств, можно сформулировать следующие уравнения:
\(\overrightarrow {АB} + \overrightarrow {BС} + \overrightarrow {СD} + \overrightarrow {DА} = \overrightarrow {АС} + \overrightarrow {СD} + \overrightarrow {DА} = \overrightarrow {AD} + \overrightarrow {DА} = \overrightarrow {AD} - \overrightarrow {AD} = \overrightarrow {0}\)
Из теоретического материала по геометрии известно, что длина нулевого вектора соответствует нулю. Полученный вывод допустимо объяснить путем логических размышлений. В процессе перемещения из одной точки четырехугольника в конечную начало и конец такого пути совпадают, что обозначает протяженность движения, равную нулю.
Ответ: 0.
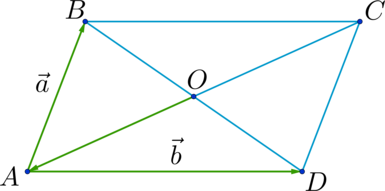
Имеется параллелограмм АВСD. Диагональные отрезки АС и BD обладают общей точкой пересечения, обозначенной за О. Предполагается, что \(\overrightarrow {АB}\) соответствует \(\overrightarrow {а}\), \(\overrightarrow {АD} равно \overrightarrow {b}\). В полученной системе х и у являются некоторыми числовыми значениями. Требуется определить сумму х и у при условии, что: \(\overrightarrow {ОА} = х \cdot \overrightarrow {а} + у \cdot \overrightarrow {b}.\)
Источник: shkolkovo.net
Решение
Обратимся к условию задания. Так как рассматриваемая геометрическая фигура является параллелограммом, целесообразно воспользоваться соответствующим правилом сложения направленных отрезков. Выполним необходимые вычисления и сформулируем окончательный ответ:
\(\overrightarrow {ОА} = \frac{1}{2}\overrightarrow {СА} = \frac{1}{2}(\overrightarrow {СВ} + \overrightarrow {ВА}) = \frac{1}{2}(\overrightarrow {DА} + \overrightarrow {ВА}) = \frac{1}{2}(-\overrightarrow {b} - \overrightarrow {a}) = -\frac{1}{2} \overrightarrow {а} -\frac{1}{2} \overrightarrow {b} \Rightarrow х = -\frac{1}{2}, у = -\frac{1}{2} \Rightarrow х + у = -1\)
Ответ: -1.
В параллелограмме АВСD точки К и L расположены на отрезках ВС и СD. При этом соблюдается пропорция ВК : КС = 3 : 1. Отметка L делит CD пополам. Вектор \(\overrightarrow {АВ} \) соответствует \(\overrightarrow {а}\), вектор \(\overrightarrow {АD}\) равен \(\overrightarrow {b}\). Требуется вычислить сумму некоторых чисел х и у, если \(\overrightarrow {KL} = х \overrightarrow \cdot {а} + у \cdot \overrightarrow {b}\).
Источник: shkolkovo.net
Решение
По условию примера задана геометрическая фигура в виде параллелограмма, составленная из направленных отрезков. Руководствуясь правилом сложения векторов, произведем соответствующие расчеты и определим искомую сумму пары числовых значений х и у. Запишем порядок вычислений:
\(\overrightarrow {KL} = \overrightarrow {KС} + \overrightarrow {СL} = \frac{1}{4}\overrightarrow {ВС} + \frac{1}{2}\overrightarrow {СD} = \frac{1}{4}\overrightarrow {AD} + \frac{1}{2}\overrightarrow {ВА} = \frac{1}{4}\overrightarrow {b} + \frac{1}{2}\overrightarrow {a} \Rightarrow х = -\frac{1}{2}, у =\frac{1}{4} \Rightarrow х + у = -0,25\)
Ответ: -0,25.
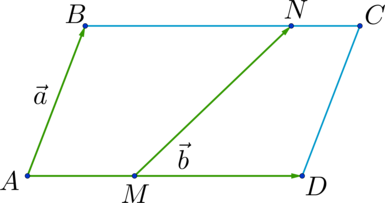
На рисунке изображен параллелограмм АВСD. На отрезках AD и ВС отмечены точки М и N таким образом, что соблюдаются соотношения:
АМ : МD = 2 : 3
ВN : NС = 3 : 1
Вектор \(\overrightarrow {АВ}\) соответствует \( \overrightarrow {а}\), направленный отрезок \( \overrightarrow {AD}\) равен \(\overrightarrow {b}\). При условии, что \(\overrightarrow {MN} = х \cdot \overrightarrow {а} + у \cdot \overrightarrow {b}\) , х и у являются некоторыми числами, требуется найти произведение \(х \cdot у\).
Источник: shkolkovo.net
Решение
По аналогии с методом решения предыдущего примера применим правило параллелограмма для вычисления необходимых величин х и у. На заключительном этапе необходимо рассчитать итоговый результат умножения. Запишем порядок расчетов:
\(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN} = \frac{2}{5}\overrightarrow {DA} + \overrightarrow {AB} + \frac{3}{4}\overrightarrow {BC} = -\frac{2}{5}\overrightarrow {AD} + \overrightarrow {AB} + \frac{3}{4}\overrightarrow {BC} = -\frac{2}{5}\overrightarrow {b} + \overrightarrow {a} + \frac{3}{4}\overrightarrow {b} = \overrightarrow {a} + \frac{7}{20}\overrightarrow {b} \Rightarrow х = 1, у =\frac{7}{20} \Rightarrow х \cdot у = 0,35\)
Ответ: 0,35.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так