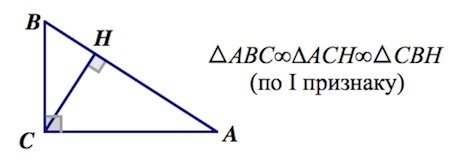Подобие треугольников: признаки и свойства
Что такое подобие треугольников
Треугольник представляет собой простую геометрическую фигуру с тремя сторонами и тремя углами. Подобные формы можно нередко встретить при решении задач на уроках геометрии. Существует ряд закономерностей и принципов, позволяющих достаточно просто при некоторых известных элементах объекта вычислять такие величины, как площадь, периметр, длины и градусные меры углов. Однако для определенных типов треугольников предусмотрены специальные правила, полезные в процессе поиска ответа на примеры в самостоятельных и контрольных работах.
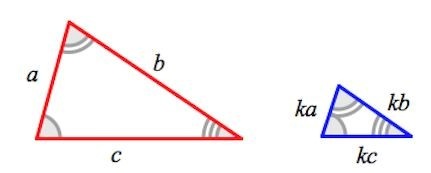
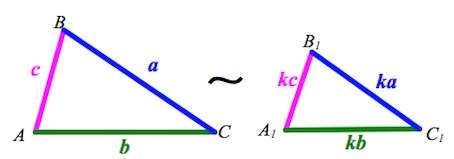
Подобные треугольники представляют собой треугольные фигуры с соответствующими равными между собой углами и пропорциональными сторонами.
Наглядное изображение подобия треугольных геометрических фигур представлено на рисунке ниже:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: egemaximum.ru
Понятие подобных треугольников предусматривает использование специальных обозначений. Рассмотрим несколько категорий, которые необходимы для детального анализа геометрических фигур. Исходя из полученных данных, можно сделать вывод о том, являются ли определенные многоугольники с тремя углами подобными. Введем определения и сформулируем для них смысловую расшифровку.
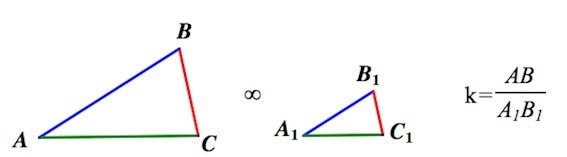
Коэффициент подобия вычисляется, как частное от деления схожих сторон, которыми обладают подобные треугольные фигуры, и обозначается числом k.
Сходственными или соответственными сторонами называют стороны, которые входят в состав подобных треугольников и расположены напротив углов с одинаковыми градусными мерами.
С целью улучшения понимания озвученных терминов изобразим перечисленные понятия на рисунке:
Источник: egemaximum.ru
Свойства подобных треугольников, формулы
Подобные треугольные фигуры характеризуются рядом специфических особенностей. С помощью свойств, которыми обладают такие объекты, достаточно просто решать задачи на вычисление тех или иных параметров треугольников. Перечислим основные из них:
- В подобных треугольных фигурах величины площадей относятся друг к другу, как коэффициент подобия, возведенный во вторую степень, то есть: \(\frac{S_{ABC}}{S1_{A1B1C1}} = k^{2}.\)
- Если определено подобие треугольных фигур, то величины их периметров относятся друг к другу, как коэффициент подобия, то есть: \(\frac{S_{ABC}}{S1_{A1B1C1}} = k.\)
- Длины любых соответствующих компонентов треугольных геометрических фигур, к примеру, биссектрис, медиан, высот, серединных перпендикуляров, относятся друг к другу, как коэффициент подобия, при условии, что треугольники являются подобными.
Признаки
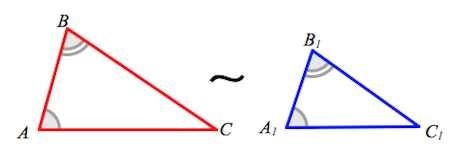
Согласно первому признаку подобия треугольных геометрических фигур, при равенстве пары углов, принадлежащих одному треугольнику, соответственно паре углов другого треугольника можно сделать вывод о подобии рассматриваемых объектов.
Источник: egemaximum.ru
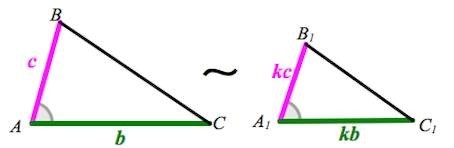
Второй признак подобия треугольных геометрических фигур подразумевает пропорциональность пары сторон одного треугольника соответственно двум сторонам второго треугольника и равенство углов, которые расположены между этими сторонами.
Источник: egemaximum.ru
По третьему признаку признают подобными такие треугольные геометрические фигуры, которые обладают пропорциональными сторонами соответственно.
Источник: egemaximum.ru
Как доказать подобие треугольников
Прежде, чем приступить к применению формул, описывающих соотношение величин в подобных треугольниках, необходимо доказать такое подобие. Подобное условие сопровождает решение многих задач по геометрии. По этой причине важно научиться не только идентифицировать подобные геометрические фигуры, но и грамотно формулировать доказательства этого свойства. С этой целью стоит рассмотреть типичные примеры, которые с высокой долей вероятностью попадаются в контрольных и самостоятельных работах.
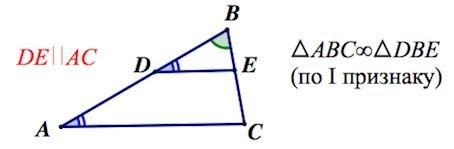
Если в треугольной геометрической фигуре проведена прямая линия параллельно относительно ее стороне, то такая прямая отсекает треугольник, который является подобным начальному. Это свойство вытекает из первого признака подобия треугольников.
Источник: egemaximum.ru
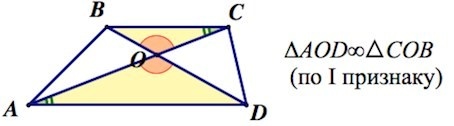
Представим, что в трапеции проведены диагонали. Изобразим озвученное условие для наглядности на рисунке ниже. Заметим, что в результате простых действий образовалось несколько треугольников. При этом треугольные геометрические фигуры, обозначенные АОD и СОВ со сторонами, равными основаниям трапеции, являются подобными. Коэффициент подобия можно в таком случае посчитать по формуле: \(\frac{АО}{ОС}\). Доказательство подобия в данной ситуации является следствием первого признака.
Источник: egemaximum.ru
В треугольной геометрической фигуре, обладающей прямоугольным углом, высота, построенная из вершины этого угла, делит фигуру на пару треугольников, каждый из которых подобен начальному. Данное свойство обусловлено первым признаком подобия треугольных геометрических фигур.
Источник: egemaximum.ru
Примеры решения задач
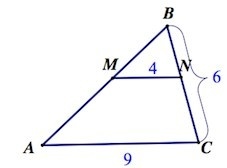
На плоскости отмечена пара точек, обозначенных за М и N. Через них проходят стороны АВ и ВС треугольной геометрической фигуры АВС. Образованная в результате несложного построения прямая линия параллельна относительно стороны АС. При условии известных величин ВС = 6, МN = 4 и АС = 9 требуется вычислить, чему равно значение CN.
Источник: egemaximum.ru
Решение
Руководствуясь первым признаком подобия треугольников, допустимо сделать вывод о подобии треугольников MBN и ABC. Это заключение объясняется наличием общего угла В, параллельностью прямых MN и AC с равными соответствующими углами BMN и BAC.
Источник: egemaximum.ru
Таким образом:
\(\frac{BN}{BC}=\frac{MN}{AC}=\frac{MB}{AB};\)
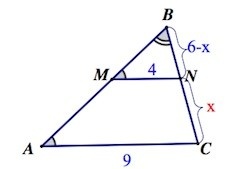
Введем обозначение NC за x. В результате BN=6-x, исходя из условий задания. Получим, что:
\(\frac{6-x}{6}=\frac{4}{9}\)
\(9(6-x)=6\cdot 4\)
\(x=\frac{10}{3}\)
\(Ответ: \frac{10}{3}.\)
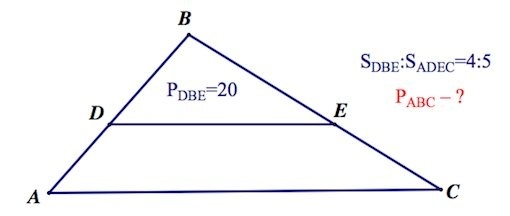
Проведена прямая линия параллельно по отношению к основанию треугольной геометрической фигуры. В результате образованы треугольник и трапеция с соотношением площадей, как 4 к 5. Новая треугольная геометрическая фигура обладает периметром, равным 20 см. Требуется найти, чему равен периметр исходного многоугольника с тремя углами.
Источник: egemaximum.ru
Решение
Исходя из информации из задания:
\(S_{DBE}:S_{ADEC}=4:5\)
В таком случае:
\(S_{DBE}:S_{ABC}=4:9 (на S_{DBE}\) приходится две пары фрагментов, на \(S_{ABC} – 4+5=9\) аналогичных элементов).
С другой стороны, DBE и ABC являются подобными по паре углов. В связи с тем, что площади треугольных геометрических фигур относятся друг к другу, как 4:9, коэффициент подобия в данном случае принимает значение 2:3. В результате:
\(P_{DBE}:P_{ABC}=2:3\)
\(P_{DBE}=20\)
\(P_{ABC}=30\)
Ответ: 30.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так