Площадь поверхности цилиндра: как найти, формула
Что такое цилиндр
Разработка инженерных чертежей зданий, сооружений, оборудования начинается с самых простых фигур геометрии. Цилиндры применяют повсеместно, что объясняет важность умения рассчитывать их основные параметры, в том числе площадь. Цилиндром также называют классический головной убор. Цилиндрическую форму имеют трубы, архитектурные компоненты зданий, посуда, разнообразные резервуары.
Использование в производстве продукции именно такой формы позволяет значительно сократить затраты. К примеру, на изготовление сосуда в виде цилиндра уходит меньше материала, чем на выпуск аналогичных товаров в форме параллелепипеда. Это объясняется разницей в величинах площади боковой поверхности материального тела.
Цилиндрические предметы удобнее держать в руках и размещать в местах хранения. По этой причине бутыли с жидкостями разного состава, которые используют в медицине, салонах красоты и других сферах, имеют цилиндрическую форму. Многие химические вещества, в том числе, газы, агрессивные среды, нефтепродукты, масла, транспортируют в цистернах в виде цилиндров. Это связано с отсутствием уязвимых мест и максимальной герметичностью подобных резервуаров. В цилиндрической емкости центр тяжести находится ниже, чем в контейнере прямоугольной формы, что обеспечивает стабильность положения заполненного резервуара. Кроме того, давление на стенки цилиндра с жидкостью или газом распределяется более равномерно.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
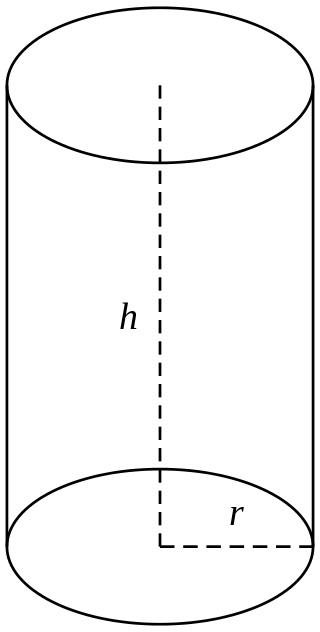
Цилиндром называют некое тело в геометрии, внутренние границы которого обозначены цилиндрической поверхностью и парой плоскостей, расположенных параллельно относительно друг друга и пересекающих эту поверхность.
Источник: ru.wikipedia.org
Разберем основные понятия, с которыми часто сталкиваются школьники в процессе решения геометрических задач. К примеру, материальное тело обладает некой поверхностью. Величину площади этой поверхности важно знать для проведения вычислений в теории и на практике.
Цилиндрическая поверхность представляет собой такую поверхность, которая сформирована с помощью параллельных прямых и некой кривой, называемой направляющей.
Цилиндр обладает основаниями, которые можно измерить. Они являются плоскими геометрическими фигурами. Для того чтобы получить основания, необходимо пересечь цилиндрическую поверхность парой плоскостей, расположенных параллельно по отношению друг к другу. Тот участок поверхности, который разделяет плоскости цилиндрических оснований, обозначают за боковую поверхность цилиндра. Плоскости оснований цилиндра высекают в своем перпендикуляре некий отрезок, называемый высотой цилиндра.
Существуют следующие виды цилиндров:
- Прямой цилиндр с основаниями в виде кругов или эллипсов. В этом случае цилиндрическая ось расположена между центральными точками симметрии и является перпендикуляром к основаниям.
- Косой цилиндр отличается от прямого геометрического тела расположением оси, то есть данный отрезок не перпендикулярен цилиндрическим основаниям.
- Круговой цилиндр имеет направляющую в виде окружности.
- Прямой круговой цилиндр (цилиндр вращения) получают в результате вращательного движения прямоугольника относительно какой-то стороны.
- Эллиптический, параболический, гиперболический цилиндры названы так по форме основания, которые имеют вид эллипсов, парабол, гипербол соответственно. В случае параболического и гиперболического цилиндров объем измеряется бесконечностью.
- Призма представляет собой цилиндр с основанием, которое обладает формой многоугольника.
- Равносторонний цилиндр является таким цилиндром вращения, в котором наблюдается равенство диаметра основания и цилиндрической высоты.
При параллельном расположении плоскостей основания и направляющей цилиндра форма границы данного основания идентична направляющей кривой.
Как найти площадь цилиндра: формула
Ознакомившись с ключевыми понятиями по теме цилиндров, можно приступить к вычислению основных параметров геометрических фигур. К примеру, в задачах по геометрии часто встречаются примеры на определение площади разных элементов цилиндра и его поверхности. Благодаря стандартным формулам, которые целесообразно использовать в процессе расчетов, значительно упрощается решение геометрических задач.
С понятием цилиндра встречаются сегодня не только школьники на уроках геометрии. Знания основных формул для расчета параметров этого геометрического тела значительно упрощает задачи инженерам и архитекторам, которые постоянно имеют дело со сложными геометрическими конструкциями с составными компонентами цилиндрической формы. Это могут быть архитектурные элементы зданий, сооружений, мостов, коммуникаций, деталей станков и оборудования. В повседневной жизни цилиндр достаточно просто разглядеть в кружке, письменных принадлежностях, тубусах для транспортировки документов.
Площадь поверхности
Рассмотрим способы нахождения площади боковой поверхности цилиндра. Данный параметр вычисляют, как произведение величины образующей и периметра сечения цилиндра плоскостью, которая является перпендикуляром к образующей.
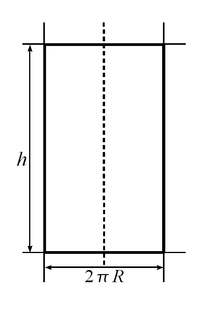
Если требуется определить площадь боковой поверхности прямого цилиндра, то необходимо ориентироваться на развертку геометрической фигуры. По форме цилиндрическая развертка является прямоугольником. Обозначим его высоту за h, а длину назовем Р. Заметим, что длина аналогична периметру основания. Таким образом, вычислить площадь боковой поверхности цилиндра можно путем расчета площади развертки этого цилиндра, то есть:
\(S_{b}=Ph\)
Представим, что R — радиус основания, которое является частью прямого кругового цилиндра. Запишем формулы для вычисления параметров такой геометрической фигуры:
\(P=2\pi R\)
\(S_{b}=2\pi Rh\)
В том случае, когда цилиндр наклонный, предусмотрена отдельная формула для расчета площади боковой поверхности. Для определения этого параметра необходимо умножить величину образующей на периметр сечения, который является перпендикуляром к образующей. Запишем соответствующую формулу:
\(S_{b}=P_{\perp }h\)
Источник: ru.wikipedia.org
Далее рассмотрим порядок вычисления площади, которой обладает полная поверхность цилиндра. Найти эту величину можно путем суммирования площадей, которыми характеризуются основания и боковая цилиндрическая поверхность. Если речь идет о прямом круговом цилиндре, то целесообразно воспользоваться следующей формулой:
\(S_{p}=2\pi Rh+2\pi R^{2}=2\pi R(h+R)\)
Площадь поперечного сечения цилиндра
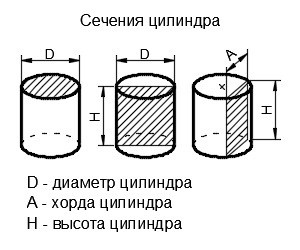
Заметим, что сечение цилиндра изображает некую фигуру, которая сформирована, если рассечь цилиндр с помощью плоскости в поперечном, либо продольном направлении.
Источник: www.center-pss.ru
Площадь цилиндрического основания можно рассчитать с помощью следующего справедливого соотношения:
\(S = \pi \cdot \frac{d^2}{4}\)
Здесь d обозначает диаметр цилиндра.
Площадь, которой обладает осевое цилиндрическое сечение, вычисляют с помощью следующей формулы:
\(S = d \cdot h\)
В данном случае d обозначает диаметр, h представляет собой высоту геометрической фигуры.
Определить, чему равна площадь сечения, которое расположено параллельно его оси сечения, то есть площадь бокового цилиндрического сечения, целесообразно с помощью следующего соотношения:
\(S = а \cdot h\)
Здесь а обозначает величину хорды цилиндрического основания, h является высотой геометрической фигуры.
Интересным фактом является история применения цилиндров в повседневной жизни людей. К примеру, по некоторым данным, в расцвет строительства городов и поселений мастера использовали бревна цилиндрической формы, чтобы упростить задачу по транспортировке тяжелых каменных элементов. Строители заметили, что именно цилиндр в роли катки существенно снижает усилия по перемещению тяжелых материалов на территории стройплощадки. Другим уникальным способом применения цилиндра в быту стали скалки, с помощью которых хозяйки раскатывали постиранное белье.
Площадь усеченного цилиндра
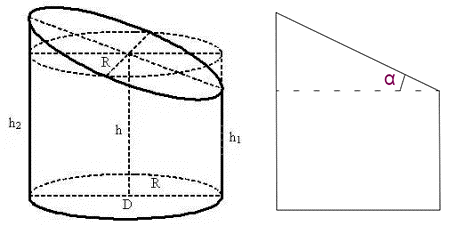
Изобразим геометрическую фигуру в виде усеченного цилиндра и обозначим ключевые ее элементы:
Источник: calcon.ru
Запишем справедливые формулы для определения площади рассматриваемой геометрической фигуры:
\(S(усеч.цил.)= \pi\cdot R \left[R+h_{1}+h_{2}+ \sqrt{R^{2}+\frac{1}{4}(h_{2}-h_{1})^{2}}\right]\)
Заметим, что:
\(h = \frac{ h_{1}+h_{2}}{2}\)
С учетом записанного равенства выполним преобразования начального уравнения:
\(S(усеч.цил.)= \frac{1}{4}\pi\cdot D \left[D+2h_{1}+2h_{2}+ \sqrt{D^{2}+ (h_{2}-h_{1})^{2}}\right]\)
Запишем следующее соотношение, вытекающее из принципов геометрии:
\(D = 2R\)
В таком случае исходную формулу допустимо записать таким образом:
\(S(усеч.цил.) = S(бок) + S(осн) + S(сеч)\)
\(S(бок) =2 \pi\cdot R\cdot h\)
\(S(осн) = \pi\cdot R^{2}\)
\(S(сеч) = \pi\cdot R^{2} \cdot \sqrt{R^{2}+ \frac{1}{4} (h_{2}-h_{1})^{2}}\)
Задачи
Успешно справиться с любой задачей по геометрии можно, если пользоваться стандартным алгоритмом действий. В первую очередь необходимо проанализировать условия примера, а именно, уточнить, какой формой обладает рассматриваемое тело, каковы ее составные элементы, какие из них обладают известными величинами. Полученную информацию целесообразно перенести на простой рисунок. Необходимо в процессе ввести буквенные обозначения для элементов геометрической фигуры. Подобные меры обеспечат корректное выявление неизвестных величин и правильный выбор подходящих формул, с помощью которых можно вычислить искомые значения.
Имеется некий цилиндр объемом \(64\pi\) . Площадь его боковой поверхности составляет \(32\pi\). Необходимо вычислить, чему равна площадь полной цилиндрической поверхности, которую разделили на \(\pi\).
Решение
Воспользуемся полученными ранее теоретическими знаниями и применим их на данном практическом примере. В первую очередь следует записать формулы, которые подходят для решения этой задачи:
\(V = \pi R^2 h\)
\(S_{\text{бок}} = 2\pi R h\)
С помощью известных характеристик геометрической фигуры вычислим величину ее радиуса. Получим, что:
\(\frac{V}{S_{\text{бок}}} = \frac{\pi R^2 h}{2\pi R h} = \frac{R}{2} = \frac{64\pi}{32\pi} = 2 \Rightarrow R = 4\)
Полная поверхность цилиндра при этом будет иметь площадь, равную сумме площадей оснований и боковой поверхности. Запишем формулу, выражающую эту зависимость, и подставим значения из условия задания:
\(S_{\text{полн}} = 2\pi R h + 2 \pi R^2 = 32\pi + 2 \cdot 16\pi = 64\pi\)
Полученный итог уменьшим в \(\pi\) раз. В результате окончательное решение равно 64.
Ответ: 64.
Некий цилиндр имеет объем \(100\pi\) . Площадь боковой цилиндрической поверхности составляет \(25\pi\). Требуется вычислить величину высоты геометрической фигуры.
Решение
На первом этапе необходимо вспомнить основные формулы для расчета объема и площади цилиндра. Запишем справедливые равенства, которые будут полезны при решении данной задачи:
\(V = \pi R^2 h\)
\(S_{\text{бок}} = 2\pi R h\)
Определим, чему равен радиус рассматриваемой геометрической фигуры путем подстановки в формулу исходных данных из условия задания:
\(\frac{V}{S_{\text{бок}}} = \frac{\pi R^2 h}{2\pi R h} = \frac{R}{2} = \frac{100\pi}{25\pi} = 4 \Rightarrow R = 8\)
Выполним преобразования соответствующего уравнения для определения высоты, которую требуется вычислить, через полученное значение радиуса:
\(V = \pi R^2 h = 64\pi h = 100\pi \Rightarrow \displaystyle h = \frac{100}{64} = 1,5625\)
Ответ: 1,5625.
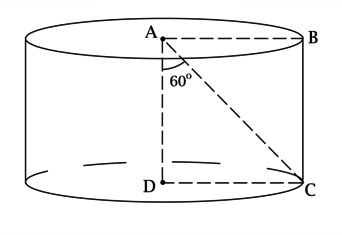
На рисунке изображена геометрическая фигура цилиндрической формы. Она характеризуется следующими параметрами:
- AD является осью;
- BC обозначает образующую;
- \(S_{ABCD} = \dfrac{16\sqrt{3}}{\sqrt[3]{\pi^2}}\)
- \(\angle CAD = 60^\circ\)
Необходимо вычислить, чему равен объем данного цилиндра.
Источник: shkolkovo.net
Решение
Проанализируем условия задачи. Заметим, что AD и BC играют роль высот геометрической фигуры. В таком случае можно прийти к выводу о том, что ABCD представляет собой прямоугольник. Руководствуясь теоретическими знаниями, запишем формулу для вычисления площади обнаруженного многоугольника:
\(S_{ABCD} = AD\cdot DC = H\cdot R = \dfrac{16\sqrt{3}}{\sqrt[3]{\pi^2}}\)
Треугольник ADC является прямоугольным. Рассмотрим эту геометрическую фигуру. Заметим, что:
\(\angle DAC = 60^\circ\)
В таком случае, получим, что:
\(AD = \mathrm{tg}\, \angle ACD\cdot DC = \mathrm{tg}\, 30^\circ\cdot R = \dfrac{R}{\sqrt{3}},\)
Таким образом, справедливым будет следующее равенство:
\(H = \dfrac{R}{\sqrt{3}}\)
\(R = \sqrt{3}H\)
Путем подстановки соотношения для поиска R в формулу, определяющую \(S_{ABCD}\), выполним следующие преобразования:
\(H^2\cdot\sqrt{3} = \dfrac{16\sqrt{3}}{\sqrt[3]{\pi^2}}\)
Исходя из записанного соотношения, допустимо сделать такой вывод:
\(H = \dfrac{4}{\sqrt[3]{\pi}}\)
\(R = \dfrac{4\sqrt{3}}{\sqrt[3]{\pi}}\)
\(V_{\text{цил}} = \pi R^2 H = \pi\cdot \dfrac{16\cdot 3}{\sqrt[3]{\pi^2}}\cdot\dfrac{4}{\sqrt[3]{\pi}} = 192\)
Ответ: 192
Цилиндр имеет объем, который вычисляется с помощью следующей формулы: \(V = \dfrac{200}{\sqrt{\pi}}\) В этой геометрической фигуре радиус основания относится к высоте, как 5. Требуется вычислить, чему равна площадь общей цилиндрической поверхности.
Источник: shkolkovo.net
Решение
Руководствуясь основными формулами для вычисления характеристик геометрической фигуры в форме цилиндра, запишем последовательное решение задачи. В первую очередь следует вычислить объем рассматриваемой фигуры:
\(V_{\text{цил}} = \pi R^2 H = \dfrac{200}{\sqrt{\pi}}\)
Согласно условию задачи:
\(\dfrac{R}{H} = 5\)
В данном случае R обозначает радиус основания цилиндра, Н представляет собой высоту этой фигуры. Тогда получим, что:
\(R = 5H\)
В результате, допустимо записать следующее соотношение:
\(\pi \cdot 25 H^3 = \dfrac{200}{\sqrt{\pi}}\qquad\Rightarrow\qquad H^3 = \dfrac{8}{\pi\sqrt{\pi}}\)
Исходя из данного равенства, можно представить формулу для определения параметров цилиндра:
\(H = \dfrac{2}{\sqrt{\pi}}\)
\(R = \dfrac{10}{\sqrt{\pi}}\)
На основании полученных данных вычислим искомую площадь геометрической фигуры:
\(S_{\text{полн}} = 2\pi R H + \pi R^2 = 2\pi R(H + R) = 2\pi\cdot\dfrac{10}{\sqrt{\pi}}\cdot\dfrac{12}{\sqrt{\pi}} = 240\)
Ответ: 240.
Цилиндр имеет основание с радиусом 7 и высоту 10. Требуется определить, чему равна площадь боковой цилиндрической поверхности, поделенная на \(\pi\).
Источник: egemaximum.ru
Решение
Запишем формулу для вычисления площади боковой поверхности цилиндра:
\(S_{bok}=2\pi RH\)
Исходя из записанного соотношения, путем подстановки известных величин найдем площадь:
\(S_{bok}=2\pi\cdot 7\cdot 10=140\pi\)
В результате получим, что:
\(\frac{S_{bok}}{\pi}=140\)
Ответ: 140.
Резервуар в форме цилиндра заполнили жидкостью до уровня 27 см. Содержимое перелили во второй резервуар с диаметром в 3 раза больше по сравнению с первым. Необходимо вычислить высоту жидкости в см во втором цилиндре.
Источник: egemaximum.ru
Решение
Обозначим радиус первой емкости цилиндрической формы за R. В таком случае радиус, который имеет второй резервуар, можно вычислить, умножив R на 3, то есть 3R. Запишем уравнение для объема жидкости в первом резервуаре:
\(V=\pi R^2\cdot 27 см^3\)
Объемы в первом и во втором случае одинаковые, поэтому:
\(V=\pi (3R)^2\cdot H\)
В результате допустимо записать следующее соотношение:
\(\pi R^2\cdot 27=\pi \cdot 9R^2\cdot H\)
\(27=9H\)
Искомая величина составит:
H=3
Ответ: 3 (см).
Емкость в форме цилиндра содержит \(600 см^3\) воды. В сосуд погрузили целиком изделие. В результате наблюдалось увеличение уровня жидкости в 1,6 раза. Требуется вычислить объем изделия.
Источник: egemaximum.ru
Решение
Заметим, что объем изделия соответствует объему жидкости, которая была вытеснена из сосуда при его погружении. Запишем соотношение для вычисления объема:
\(V=S_{osnov}\cdot H\)
С помощью условий задания составим справедливое равенство:
\(600=S_{osnov}\cdot H\)
В результате можно посчитать, какой объем составляет вытесненная жидкость, а, следовательно, и изделие:
\(V_{detal}=S_{osnov}\cdot 0,6H=0,6(S_{osnov}\cdot H)=0,6\cdot 600=360\)
Ответ: 360.
Некую емкость в форме цилиндра заполнили жидкостью в количестве 2000 куб. см. Уровень, на котором находится край жидкости, составляет 12 см. В жидкую среду поместили какую-то конструкцию. В результате наблюдался подъем уровня на 9 см. Необходимо вычислить объем, который имеет конструкция.
Решение
Вспомним закономерное соотношение, которое подразумевает равенство объема конструкции величине объема воды, которая была таким способом вытеснена из резервуара. Исходя из условия задания, можно прийти к выводу, что вытесненный объем составляет 9/12 от начального:
\(V_дет = \frac{9}{12}\cdot 2000 = \frac{3}{4}\cdot 2000 = 1500\)
Ответ: 1500 куб. см.
Цилиндрическое тело обладает основой, радиус которой составляет 2. Высота рассматриваемого цилиндра равна 3. Необходимо вычислить, чему соответствует значение площади боковой поверхности фигуры, поделенное на \(\pi\) .
Решение
Воспользуемся закономерностями для расчета параметров цилиндра, которые знакомы из курса теории. Запишем, каким образом можно рассчитать площадь боковой поверхности цилиндрической фигуры:
\(S = 2\pi \cdot r \cdot H\)
Обратимся к условию задания, чтобы подставить в формулу численные значения величин и выполнить вычисления:
\(S = 2\pi \cdot 2 \cdot 3 = 12 \pi\)
Полученный результат требуется разделить на \pi и записать ответ к задаче.
Ответ: 12.
Имеется некое тело цилиндрической формы. В основании цилиндра можно заметить окружность длиной 3. Высота рассматриваемой геометрической фигуры равна 2. Необходимо вычислить значение площади, которой характеризуется боковая поверхность цилиндрического тела.
Решение
Воспользуемся справедливыми соотношениями для определения элементов цилиндра, которые знакомы из теоретического курса. Составим формулу, демонстрирующую, каким образом можно вычислить площадь боковой поверхности цилиндрического объекта:
\(S = 2\pi \cdot r \cdot H = Сh\)
В данном случае С является обозначением длины окружности основания цилиндра.
Путем подстановки численных значений из условия задачи найдем искомую величину:
\(S = 3 \cdot 2 = 6\)
Ответ: 6.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так