Что нужно знать о площади треугольника — основные сведения
- Что такое площадь треугольника
- Общие формулы вычисления, подходящие для разных видов треугольников
- Формулы для вычисления площади прямоугольного треугольника
- Формулы для вычисления площади равнобедренного треугольника
- Формулы для вычисления площади равносторонних треугольников
- Примеры решения задач по данной теме
Что такое площадь треугольника
Треугольник представляет собой геометрическую фигуру при рассмотрении ее в евклидовом пространстве, сформированную с помощью трех отрезков, которые соединяют три точки, не принадлежащие одной прямой.
Указанные точки являются вершинами треугольника. Отрезки играют роль сторон треугольника.
Площадь треугольника является одним из параметров замкнутой геометрической фигуры в виде треугольника, характеризующим его размер.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Общие формулы вычисления, подходящие для разных видов треугольников
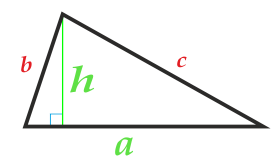
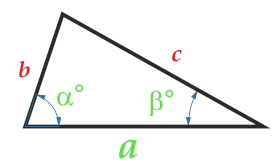
Площадь треугольника можно определить, зная, чему равны его основание и высота:
\(S = \frac{1}{2} a\cdot h,\)
где а является основанием (при выборе основания можно использовать любую из сторон треугольника), h обозначает высоту треугольника.
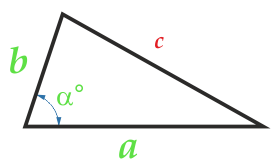
Если известны величины двух сторон, а также градусная мера угла, который заключен между этими сторонами, площадь треугольника вычисляется таким образом:
\(S = \frac{1}{2} a\cdot b \cdot \sin\alpha\)
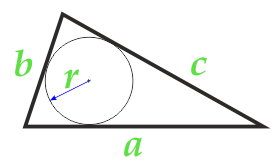
Если треугольник описан около окружности, то его площадь можно определить, зная радиус вписанной окружности и стороны треугольника:
\(S = r\cdot \frac{P}{2} = r\cdot \frac{a+b+c}{2}\)
Здесь r является радиусом вписанной окружности.
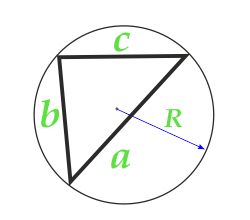
Если треугольник вписан в окружность, то его площадь можно вычислить таким образом:
\(S = \frac{a\cdot b\cdot c}{4R},\)
где R обозначает радиус описанной около треугольника окружности.
Вычисление площади треугольника с помощью формулы Герона:
\(S = \sqrt{p(p-a)(p-b)(p-c)}\)
Формула для определения площади какого-либо произвольного треугольника по стороне и двум прилежащим углам:
\(S = \frac{a^2}{2} \cdot \frac{\sin\alpha \cdot \sin \beta}{\sin(180-(\alpha + \beta))}\)
Формулы для вычисления площади прямоугольного треугольника
Формула для расчета площади прямоугольного треугольника, если известны длины двух его катетов:
\(S = \frac{1}{2}\cdot a\cdot b\)
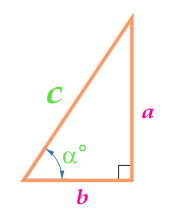
Площадь прямоугольного треугольника можно вычислить с помощью гипотенузы и угла по формуле:
\(S = \frac{1}{4} \cdot c^2 \cdot \sin(2\alpha)\)
Если известен катет и угол, то можно вычислить площадь прямоугольного треугольника таким образом:
\(S = \frac{1}{2} \cdot b^2 \cdot tg (\alpha)\)
В прямоугольный треугольник можно вписать окружность. Тогда площадь этого треугольника определяется по отрезкам, на которые вписанная окружность делит гипотенузу:
\(S = d\cdot e\)
Формула расчета площади прямоугольного треугольника с помощью гипотенузы и вписанной окружности:
\(S = r \cdot (r+c),\)
где с обозначает гипотенузу, а r является радиусом вписанной окружности.
Формула Герона для вычисления площади прямоугольного треугольника:
\(S = (p-a)\cdot (p-b)\)
Формулы для вычисления площади равнобедренного треугольника
Если известны длины боковых сторон и основания равнобедренного треугольника, то для вычисления его площади целесообразно использовать следующую формулу:
\(S = \frac{c}{4} \cdot \sqrt{4\cdot a^2-c^2}\)
Когда известны длины боковых сторон равнобедренного треугольника и величина угла, лежащего между этими сторонами, формула для определения площади примет такой вид:
\(S = \frac{1}{2}a^2\sin(\alpha)\)
Формула для определения площади равнобедренного треугольника с помощью боковой стороны, основанию и углу, который расположен между ними:
\(S = \frac{1}{2}a\cdot c\cdot \sin(\beta)\)
При известном основании и величине угла, который расположен между боковыми сторонами, площадь равнобедренного треугольника вычисляется таким образом:
\(S = \frac{c^2}{4\cdot tg(\frac{\alpha}{2})}\)
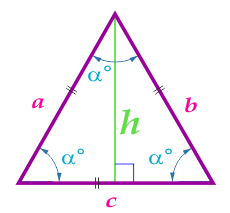
Формула площади равнобедренного треугольника по высоте и основанию:
\(S = \frac{1}{2} \cdot c \cdot h\)
Формулы для вычисления площади равносторонних треугольников
Если известна сторона в равностороннем треугольнике, то его площадь можно вычислить следующим образом:
\(S = \frac{\sqrt{3}}{4} a^2\)
При известной высоте равностороннего треугольника его площадь вычисляется по формуле:
\(S = \frac{h^2}{\sqrt{3}}\)
Источник: doza.pro
В равносторонний треугольник можно вписать окружность. Тогда площадь такого треугольника определяется по формуле:
\(S = 3\sqrt{3} \cdot r^2,\)
где r обозначает радиус вписанной окружности.
Формула площади равностороннего треугольника по радиусу описанной около него окружности:
\(S = \frac{3 \sqrt{3}}{4}\cdot R^2,\)
где R обозначает радиус описанной окружности.
Примеры решения задач по данной теме
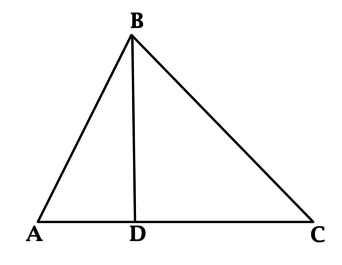
Треугольник АВС с высотой ВD характеризуется следующими параметрами:
AD = 1
DC = 3
\(\angle DBC = 45^{\circ}\)
Нужно определить, чему равна площадь этого треугольника.
Решение
\(\angle BCD = 90^{\circ} - \angle DBC = 45^{\circ} = \angle DBC\)
\(BD = DC = 3\)
Зная, что площадь треугольника вычисляется, как половина произведения основания на высоту, которая проведена к этому основанию, запишем следующее:
\(S = 0,5 \cdot (3 + 1) \cdot 3 = 6\)
Ответ: 6.
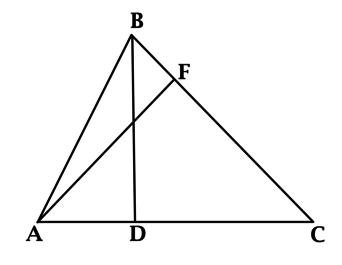
Имеется треугольник АВС с высотами AF и BD. При этом AF = 4, BD = 3, AC = 6. Требуется вычислить ВС.
Решение
Вспомним, что площадь треугольника вычисляется, как половина произведения основания на высоту, которая проведена к этому основанию. При расчете площади можно выбрать в качестве основания любую сторону, тогда:
\(0,5 \cdot AC \cdot BD = 0,5 \cdot BC \cdot AF\)
В результате:
\(9 = 0,5 \cdot BC \cdot 4\)
Таким образом:
\(BC = 4,5\)
Ответ: 4,5.
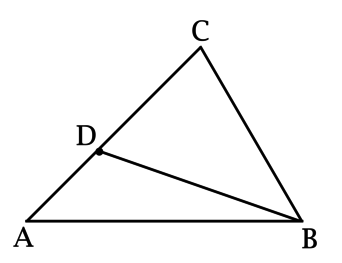
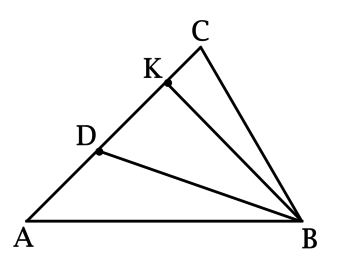
На рисунке представлен треугольник АВС, в котором точка D расположена на AC. При этом:
\(\dfrac{AD}{DC} = \dfrac{2}{3}\)
Требуется вычислить площадь треугольника BCD, если площадь треугольника ABD равна 7,5.
Решение
Проведем высоту ВК:
Запишем формулу для определения площади треугольника ABD:
\(S_{ABD} = 0,5\cdot AD\cdot BK\)
Аналогичным образом можно посчитать:
\(S_{BCD} = 0,5\cdot CD\cdot BK\)
В результате:
\(\dfrac{S_{BCD}}{S_{ABD}} = \dfrac{0,5\cdot CD\cdot BK}{0,5\cdot AD\cdot BK} = \dfrac{CD}{AD} = \dfrac{3}{2}, тогда S_{BCD} = \dfrac{3}{2}\cdot S_{ABD} = \dfrac{3}{2}\cdot 7,5 = 11,25\)
Ответ: 11,25.
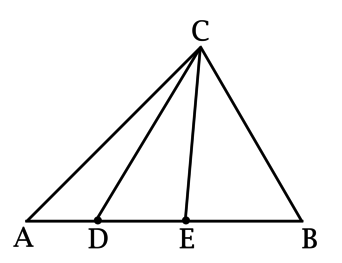
Имеется некий треугольник АВС с точками D и E, принадлежащими отрезку АВ. При этом:
\(\dfrac{AD + BE}{AB} = \dfrac{2}{3}\)
Площадь треугольника ACD равна 10, а также выполняется следующее условие:
\(\dfrac{S_{CEB}}{S_{CED}} = \dfrac{6}{5}.\)
Необходимо вычислить площадь треугольника ABC.
Решение
Предположим, что h является длиной высоты, которую опустили из точки С на отрезок АВ. В таком случае:
\(S_{ABC} = 0,5\cdot AB\cdot h\)
\(S_{CEB} = 0,5\cdot EB\cdot h, S_{CED} = 0,5\cdot DE\cdot h\)
В результате:
\(\dfrac{6}{5} = \dfrac{S_{CEB}}{S_{CED}} = \dfrac{0,5\cdot EB\cdot h}{0,5\cdot DE\cdot h} = \dfrac{EB}{DE}\)
С другой стороны:
\(DE = AB - (AD + BE) = AB - \dfrac{2}{3}\cdot AB = \dfrac{1}{3}\cdot AB\)
Таким образом:
\(EB = \dfrac{6}{5}\cdot \dfrac{1}{3}\cdot AB = \dfrac{2}{5}\cdot AB\)
\(AD = AB - (DE + EB) = AB - \dfrac{1}{3}\cdot AB - \dfrac{2}{5}\cdot AB = \dfrac{4}{15}\cdot AB\)
\(10 = S_{ACD} = 0,5\cdot AD\cdot h = 0,5\cdot \dfrac{4}{15}\cdot AB\cdot h = \dfrac{4}{15}\cdot S_{ABC}\)
\(S_{ABC} = 10\cdot\dfrac{15}{4} = 37,5\)
Ответ: 37,5.
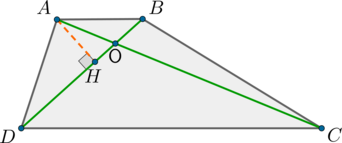
В трапеции ABCD точка О является точкой пересечения диагоналей. DC обозначает самое большое из оснований трапеции. Площадь образованного при этом треугольника ADO составляет 12, а отрезок DO равен 2BO. Требуется вычислить площадь трапеции.
Решение
\(S_{ADO} = 0,5\cdot 2BO\cdot OH\Rightarrow S_{AOB} = 0,5\cdot BO\cdot OH =12 : 2 = 6\)
AB\parallel DC
Таким образом, треугольники AOB и DOC являются подобными с коэффициентом k:
\(k = \dfrac{DO}{BO} = 2\Rightarrow \dfrac{S_{DOC}}{S_{AOB}}= k^2 = 4\)
\(S_{DOC} = 6\cdot 4 =24\)
\(S_{BOC} = S_{AOD} = 12\)
\(S_{ABCD} = S_{AOD} + S_{AOB} + S_{DOC} + S_{BOC} = 54\)
Ответ: 54.
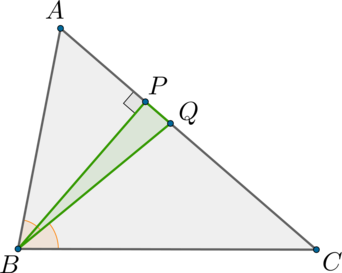
Треугольник АВС образован тремя сторонами:
AB=26
BC=30
AC=28
Требуется рассчитать, чему равна площадь треугольника, который заключен между биссектрисой и высотой, проведенными из вершины B.
Решение
Представим, что BP обозначает высоту, а BQ является биссектрисой рассматриваемого треугольника. Воспользуемся формулой Герона для нахождения площади:
\(S_{ABC} = \sqrt{42\cdot(42 - 30)(42 - 28)(42 - 26)}=14\cdot6\cdot4 = 336\)
Найдем площадь треугольника ABC, зная высоту:
\(S_{ABC} = \dfrac{AC\cdot BP}2\)
В таком случае:
\(BP = \dfrac{2\cdot S_{ABC}}{AC} = \dfrac{2\cdot 336}{28} = 24\)
Согласно свойству биссектрисы:
\(\dfrac{AQ}{QC} = \dfrac{AB}{BC} = \dfrac{13}{15}\)
В результате:
\(AQ = \dfrac{13}{28}\cdot AC =13\)
Исходя из теоремы Пифагора, запишем следующее равенство для прямоугольного треугольника АРВ:
\(AP = \sqrt{AB^2-BP^2} = \sqrt{26^2-24^2} = 10\)
Таким образом:
\(PQ = AQ - AP = 13-10=3\)
\(S_{BPQ} = \dfrac{1}2 \cdot PQ \cdot BP = \dfrac{3\cdot 24}2 = 36\)
Ответ: 36.
В треугольнике АВС отметили точку Н с какими-то координатами, которая делит отрезок АВ, как \(\dfrac{2}3\), считая от вершины B. Площадь треугольника АВС составляет 15. Нужно вычислить площадь треугольника HBC.
Решение
Заметим, что треугольники ABC и HBC обладают общим углом В. В таком случае:
\(\dfrac{S_{HBC}}{S_{ABC}} = \dfrac{HB\cdot BC}{AB\cdot BC} = \dfrac{HB}{AB}\)
Предположим, что:
\(HB = 2x\)
\(AH = 3x\)
Зная, что AB = HB + AH, запишем следующее равенство:
\(\dfrac{HB}{AB} = \dfrac{2x}{2x+3x} = \dfrac{2}5 \quad\Rightarrow \quad S_{HBC} = S_{ABC} \cdot \dfrac{2}5 = 6\)
Ответ: 6.
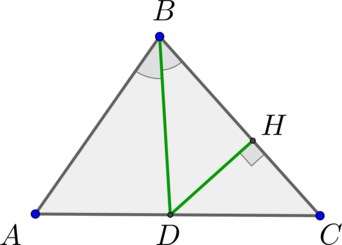
В треугольнике АВС отрезок BD обозначает биссектрису. При этом BC = 6, AB = 4. В треугольнике DBC высота DH = 3. Требуется высчитать площадь треугольника ABC.
Заметим, что с помощью биссектрисы треугольник АВС поделен на два треугольника, которые имеют по одному равному углу. В таком случае, площади этих треугольников соотносятся как произведения сторон, которые образуют данные углы:
\(\dfrac{S_{ABD}}{S_{DBC}} = \dfrac{AB\cdot BD}{BC\cdot BD} = \dfrac{AB}{BC}\)
Вычислим площадь треугольника BDC:
\(S_{DBC} = \dfrac{1}2\cdot DH\cdot BC = \dfrac{1}2\cdot 3\cdot 6 = 9\)
Определим, чему равна площадь треугольника ABD, согласно ранее записанному отношению:
\(S_{ABD} = \dfrac{4}6\cdot S_{DBC} = \dfrac{4}6\cdot 9 = 6\)
Площадь треугольника АВС складывается из площадей двух треугольников ABD и DBC:
\(S_{ABC} = S_{ABD} + S_{DBC} = 6 + 9 =15\)
Ответ: 15.
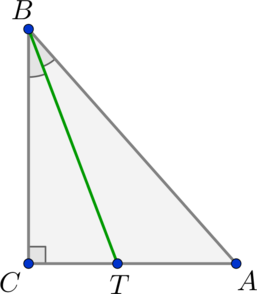
В треугольнике АВС угол С является прямым. Отрезок ВТ обозначает биссектрису, а AT = 15 и TC = 12. Необходимо узнать, чему равна площадь треугольника АВТ.
Решение
Исходя из свойства биссектрисы:
\(\dfrac{TC}{BC} = \dfrac{AT}{AB}\)
Введем следующие обозначения:
BC = x
AB = y
В таком случае:
\(\dfrac{12}x = \dfrac{15}y\Rightarrow x = 0,8\cdot y\)
Воспользуемся теоремой Пифагора для треугольника ABC и сделаем следующий вывод:
\(x^2+27^2 = y^2\Rightarrow 0,64\cdot y^2 + 27^2 = y^2\Rightarrow y = 45, x = 36\)
\(S_{ABT} = 0,5\cdot AT\cdot BC = 0,5\cdot 15\cdot 36 = 270\)
Ответ: 270.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так