Как вычисляется площадь трапеции
Что такое трапеция
Трапеция представляет собой четырехугольную геометрическую фигуру с двумя параллельными относительно друг друга сторонами, а две другие стороны не являются параллельными.
Ознакомиться с наглядным изображением трапеции можно с помощью рисунка, который расположен ниже. На изображении представлены основные типы трапециевидной геометрической фигуры:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: egemaximum.ru
Трапеция состоит из нескольких элементов. Стороны, которые расположены параллельно относительно друг друга, называют основаниями. Другие две стороны являются боковыми сторонами.
Как рассчитать площадь трапеции: формулы
При изучении основ геометрии можно нередко встретить примеры, где необходимо вычислить площадь трапеции. Решение подобных заданий реализовано по стандартному алгоритму. Таким образом, на первом этапе следует ознакомиться с условиями задачи, определить известные и неизвестные величины, идентифицировать тип геометрической фигуры, о которой идет речь. Затем, основываясь на собранной информации, стоит подобрать подходящее математическое соотношение для вычисления неизвестных величин через известные элементы трапеции.
Через основания и высоту
Источник: max-calc.ru
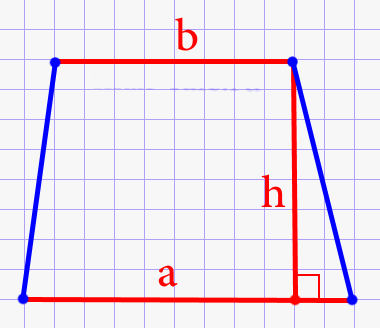
\(S = \frac{a+b}{2}\cdot h\)
При записи этой формулы использованы обозначения основных элементов геометрической трапециевидной фигуры. В этом случае а и b соответствуют основаниям трапеции, которые обозначены на рисунке выше. Можно заметить, что эти стороны параллельны относительно друг друга. Буквой h здесь обозначена высота.
Через высоту и среднюю линию
Источник: max-calc.ru
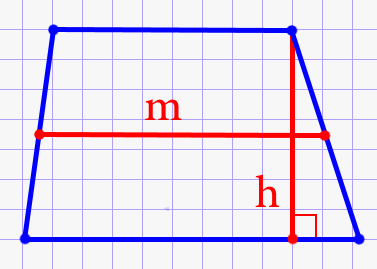
\(S = m \cdot h\)
В данном математическом соотношении m является средней линией трапеции. Из названия понятно, что такая прямая проходит через середину геометрической фигуры. С целью построения этого отрезка необходимо поделить боковые стороны ровно пополам и через точки провести линию, как показано на рисунке выше.
Через диагонали и угол между ними
Источник: max-calc.ru
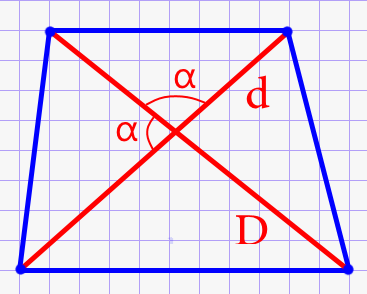
\(S = \frac{Dd}{2}\cdot \sin \alpha\)
Воспользоваться записанной формулой на практике несложно, если построить в трапециевидной геометрической фигуре диагонали. На рисунке они обозначены разными буквами, чтобы исключить путаницу.
Через четыре стороны
Источник: max-calc.ru
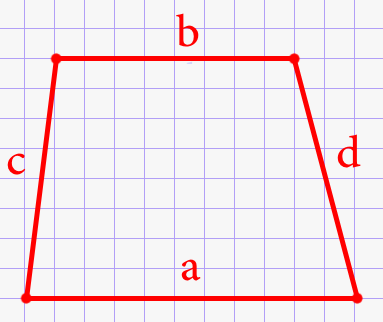
\(S = \frac{a+b}{2}\cdot \sqrt{c^{2}-(\frac{(a-b)^{2}+c^{2}-d^{2}}{2(a-b)})^{2}}\)
Примеры решения задач
Перед тем, как приступить к тренировке на практике, стоит воспроизвести стандартный алгоритм действий. В первую очередь необходимо внимательно проанализировать условия задания. Когда идентифицированы элементы геометрической фигуры и определены их величины, можно переходить к подбору подходящего математического соотношения. С помощью формул достаточно просто найти неизвестные компоненты трапеции через взаимосвязанные с ними величинами. На заключительной стадии предполагается подстановка численных значений в выражения для вычисления окончательного ответа.
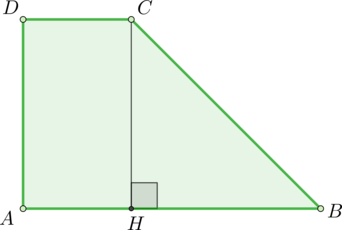
На рисунке изображена трапеция с прямым углом. В данной геометрической фигуре основания составляют 6 и 2. Боковая сторона с максимальной величиной образует вместе с основанием угол в 45 градусов. Требуется определить, чему равна площадь рассматриваемой трапециевидной фигуры.
Источник: oge.shkolkovo.net
Решение
Проанализируем изображение трапеции. На рисунке обозначены все данные по условию задания величины. Однако его можно дополнить, что позволит существенно упростить дальнейшие вычисления. Построим высоту CH.
Источник: oge.shkolkovo.net
Заметим, что градусная мера \(\angle HBC\) составляет \(45^\circ\). В результате:
\(\angle HCB=45^\circ\)
Таким образам, целесообразно сделать вывод о том, что \(\triangle HBC\) является равнобедренным. Из чего следует такое равенство:
HB=HC
Тогда геометрическая фигура ADCH является прямоугольником. По этой причине справедливо следующее равенство:
AH=DC=2
В результате:
CH=HB=6-2=4
Запишем формулу для вычисления площади трапециевидной фигуры, которая больше всего подходит для данного случая. Подставив численные значения из условия задания, вычислим окончательный ответ:
\(S=\dfrac{AB+DC}2\cdot CH=\dfrac{2+6}2\cdot 4=16\)
Ответ: 16.
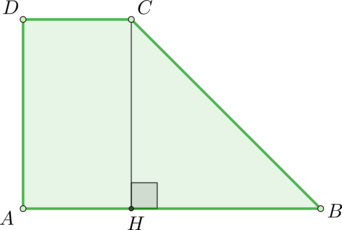
Дана прямоугольная трапеция. Ознакомиться с ее изображением можно на рисунке ниже. Основания этого объекта составляют 12 и 4. Площадь фигуры соответствует 64. Требуется вычислить градусную меру острого угла, расположенного внутри рассматриваемой трапеции.
Источник: oge.shkolkovo.net
Решение
Начать решение этого примера следует с изучения наглядного изображения трапеции. Заметим, что, как и в предыдущем задании, здесь целесообразно выполнить дополнительное построение. Если провести высоту СН, то дальнейшие расчеты значительно упрощаются.
Источник: oge.shkolkovo.net
Заметим, что в результате дополнительных манипуляций с рисунком геометрической фигуры получился прямоугольник ADCH. Запишем вытекающее из этого условия равенство:
HB=12-4=8
Воспользуемся формулой для вычисления площади трапеции и выразим через нее неизвестную величину:
\(64=\dfrac{AB+DC}2\cdot CH=\dfrac{4+12}2\cdot CH\quad\Rightarrow\quad\)
CH=8
Таким образом:
CH=HB=8
В результате \(\triangle CHB\) представляет собой равнобедренный треугольник с равными углами, расположенными около его основания. Запишем соответствующее математическое соотношение:
\(\angle HCB=\angle HBC\)
Исходя из того, что при сложении острых углов в прямоугольном треугольнике получается 90 градусов, можно записать следующее справедливое равенство:
\(\angle B=\angle HBC=90^\circ\div2=45^\circ\)
Ответ: 45.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так