Как вычислить площадь равнобедренного треугольника

Равнобедренный треугольник — это

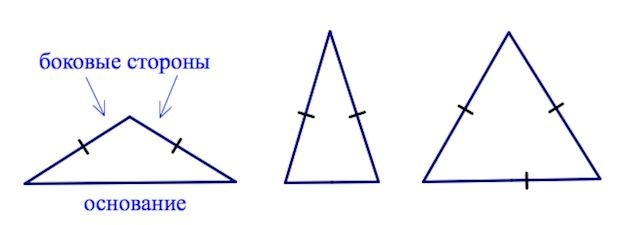
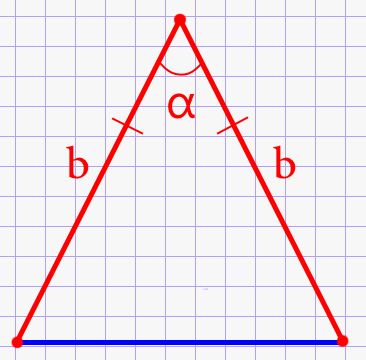
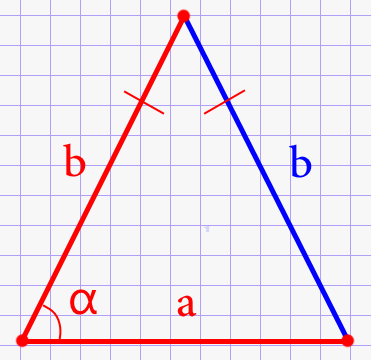
В данном случае стороны с одинаковыми величинами носят название «боковые». Третью сторону именуют основанием. Наглядно эти обозначения представлены на рисунке ниже:

Источник: egemaximum.ru

Задачи на вычисление элементов и параметров равнобедренного треугольника часто встречаются в курсе геометрии. Однако прежде, чем приступить к исследованию формул, предусмотренных для такого объекта, необходимо научиться его правильно идентифицировать. Помогут в этом следующие признаки:

1. Многоугольник с тремя углами, два из которых обладают одинаковыми градусными мерами, является равнобедренным треугольником.
2. Когда в треугольной фигуре линия медианы совпадает с высотой, а также биссектрисой, треугольник считают равнобедренным.

Как найти площадь: формулы

На первый взгляд задача на вычисление площади равнобедренного треугольника кажется довольно сложной. С помощью ряда закономерностей расчеты значительно упрощаются. Существует ряд математических соотношений, описывающих взаимосвязь между элементами треугольной фигуры с парой равных сторон и ее площадью. Рассмотрим наиболее часто встречающиеся в задачах по геометрии примеры таких формул.

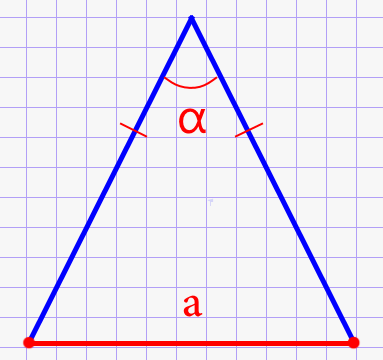
Через основание и угол между боковыми сторонами

Источник: max-calc.ru

\(S=\frac{a^{2}}{4\cdot tg\frac{\alpha}{2}}\)

В записанной формуле а обозначает основание треугольника, \(\alpha\) равно углу, который расположен между боковыми сторонами.

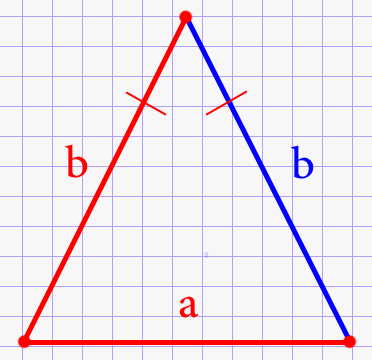
Через сторону и основание

 

Источник: max-calc.ru

\(S=\frac{a}{4}\sqrt{4\cdot b^{2} - a^{2}}\)

Заметим, что в представленном выше соотношении а является основанием, а b играет роль одной из боковых сторон треугольника.

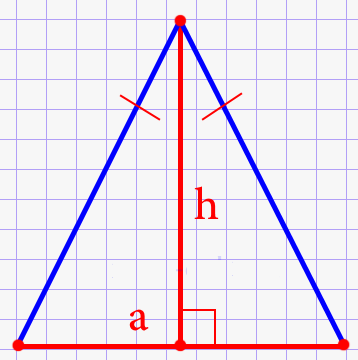
Через основание и высоту

 

Источник: max-calc.ru

\(S=\frac{1}{2}ah\)

В данном соотношении встречается другое обозначение, которое ранее не было использовано в предыдущих формулах. Буквой h подписывают высоту. В результате для вычисления площади равнобедренной треугольной фигуры необходимо результат от умножения основания и высоты поделить пополам.

Через боковые стороны и угол меду ними

 

Источник: max-calc.ru

\(S=\frac{1}{2}b^{2}\cdot \sin (\alpha)\)

Эта формула полезна, когда в задании на вычисление значения площади геометрической фигуры дана величина угла. В этом математическом соотношении угол обозначен \(\alpha\). Рассматриваемый элемент отмечен на изображении выше для наглядности.

Через основание, сторону и угол между ними

 

Источник: max-calc.ru

\(S=\frac{1}{2}ab \cdot \sin (\alpha)\)

В записанной выше формуле собрано сразу три элемента, составляющих равнобедренный треугольник. Они обозначены на рисунке. Таким образом, для вычисления площади равнобедренной треугольной фигуры необходимо вычислить, чему равен синус угла \(\alpha\), перемножить найденное значение с боковой стороной и основанием, а полученный итог затем поделить пополам. 

Примеры решения задач

Описанные выше математические закономерности значительно упрощают решение задач по геометрии. Таким образом, если в задании речь идет о равнобедренном треугольнике, то целесообразно начать с разбора условия. После того как идентифицированы все элементы геометрической фигуры с известными и неизвестными значениями, можно правильно выбрать необходимую формулу. Далее остается лишь путем подстановки найти искомую величину и записать ответ. В качестве тренировки попробуем справиться с несколькими типичными примерами.

Решение

Вспомним из теоретической части, что площадь данного треугольника можно вычислить, как половину от результата умножения сторон на синус угла между ними. Известно, что в равносторонней треугольной фигуре градусная мера углов равна 60 градусам, а стороны обладают одинаковым величинами. В данном случае стороны составляют по 10. Исходя из начальных данных, запишем подходящую формулу и выполним вычисления:

\(S=\frac{1}{2}10 \cdot 10\cdot \sin (60)= 25\sqrt{3}\)

Обратимся повторно к условию задачи. Заметим, что перед тем, как записать окончательный ответ, необходимо выполнить деление искомого значения на \(\sqrt{3}\). В результате итог составит 25.

Ответ: 25

Решение

Известно, что в равностороннем треугольнике каждая сторона имеет такую же длину, как и остальные. Таким образом, при периметре, равным 30, любая из сторон рассматриваемой геометрической фигуры составляет 10. Еще одно важное свойство, которым обладает равносторонний треугольник, заключается в равенстве его углов между собой и 60 градусам. Из курса теории вспомним, что площадь треугольника равна половине произведения сторон на синус угла между ними. Остается лишь подставить значения из условия заданий и выполнить расчет:

\(S=\frac{1}{2}10 \cdot 10\cdot \sin (60)= 25\sqrt{3}\)

На этом расчеты не заканчиваются. По условию примера требуется найти результат от деления площади на \(\sqrt{3}\). В результате получим значение 25.

Ответ: 25

Решение

При известной высоте в равностороннем треугольнике несложно вычислить величину стороны. С этой целью можно воспользоваться следующей формулой:

\(h = a\frac{\sqrt{3}}{2}\)

Подставим значение из условия задачи и вычислим результат:

\(h = 10 \frac{\sqrt{3}}{2} = \frac{2}{\sqrt{3}}\)

Известно, что площадь треугольника равна половине произведения сторон на синус угла между ними. В результате получим:

\(h = \frac{1}{2}\frac{20}{\sqrt{3}}\frac{20}{\sqrt{3}}\cdot \sin 60° = \frac{100\sqrt{3}}{3}\)

На следующем этапе решения целесообразно выполнить заключительное действие. Оно состоит в делении величины высоты на \(\frac{\sqrt{3}}{3}\). Таким образом, в ответ можно записать 100.

Ответ: 100.