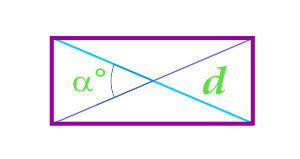Что нужно знать о площади прямоугольника — основные сведения
Что такое площадь
Площадь является одним из параметров замкнутой геометрической фигуры, который характеризует ее размер.
Площадь обозначают буквой S.
Часто в задачах указаны площади фигур в разных единицах подсчета. В таком случае перед нахождением величин и действиями с ними необходимо привести их к одной единице измерения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Площадь можно измерить в следующих единицах:
- миллиметры в квадрате \((мм^{2})\);
- квадратные сантиметры \((см^{2})\);
- дециметры в квадрате \((дм^{2})\);
- квадратные метры \((м^{2})\);
- километры в квадрате \((км^{2})\);
- гектары (га).
Самые простые формулы для вычисления площади
Прямоугольником называют такой четырехугольник, который имеет пару равных противолежащих сторон и одинаковые по величине четыре угла.
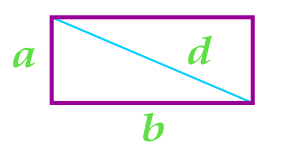
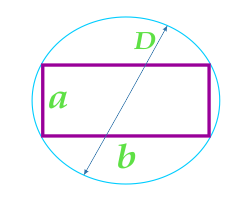
Изобразим четырехугольник с высотой а и длиной b:
Существует две распространенные и наиболее простые формулы с произведением и делением величин, с помощью которых высчитывается площадь прямоугольника.
\(S = a \cdot b\)
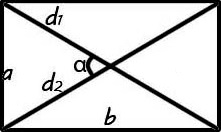
\(S = \frac{d^{2}}{2}\sin\alpha\)
Здесь а обозначает ширину прямоугольника, b выражает длину геометрической фигуры, d является диагональю, \(\alpha \) представляет собой угол, расположенный между диагоналями четырехугольника.
Площадь прямоугольника представляет собой положительную величину, измеряющую часть плоскости, занятой прямоугольником.
Формулы для вычисления площади прямоугольника через диагонали
Площадь прямоугольника вычисляют по известной диагонали и стороне. Посчитать данный параметр можно с помощью формулы:
\(S = a \cdot \sqrt{d^2 - a^2}\)
Если известны диагонали прямоугольника и мера угла, который расположен между этими диагоналями, то площадь геометрической фигуры можно рассчитать таким образом:
\(S = \frac{d^{2}\cdot\sin\alpha}{2}\)
Формулы для вычисления площади прямоугольника через описанную окружность
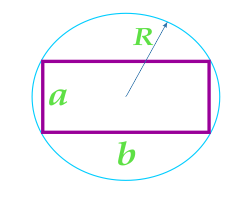
Когда известна сторона прямоугольника и величина радиуса окружности, описанной около такого прямоугольника, площадь геометрической фигуры рассчитывают по формуле:
\(S = a \cdot \sqrt{4 \cdot R^2 - a^2}\)
Другой способ расчета площади прямоугольника состоит в применении формулы, в которую включены стороны фигуры и диаметр описанной около прямоугольника окружности:
\(S = a \cdot \sqrt{D^2 - a^2}\)
Примеры решения задач по данной теме
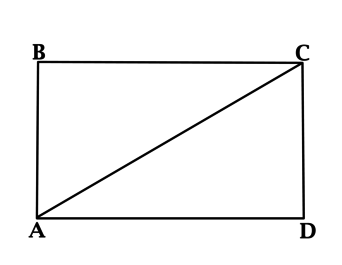
Дан прямоугольник ABCD, в котором сторона AB = \dfrac{2}{5}BC, а периметр ABCD составляет 42. Требуется вычислить, чему равна площадь треугольника АВС.
Решение
Допустимо считать, что прямоугольник представляет собой частный случай параллелограмма. Сделаем вывод о равенстве его противоположных сторон. При этом:
\(2\cdot AB + 2\cdot BC = 42\)
Заметим, что:
\(AB = \dfrac{2}{5}BC\)
Сформулируем равносильное выражение:
\(\dfrac{4}{5}BC + 2\cdot BC = 42\)
В результате:
\(BC = 15\)
\(AB = 6\)
Треугольники являются равными по теореме о двух катетах. Данные фигуры обладают одинаковыми площадями. В результате площадь треугольника АВС исчисляется половиной площади прямоугольной формы ABCD:
\(0,5\cdot 6\cdot 15 = 45\)
Ответ: 45.
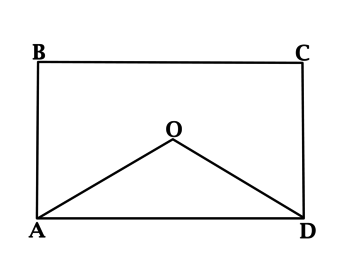
Обозначим за О точку, в которой пересекаются диагонали, проведенные в прямоугольнике \(ABCD\). При этом \(\angle OAD = 28^{\circ}\). Необходимо определить градусную меру \(\angle AOD\).
Решение
При пересечении диагонали делятся на две равные части с помощью точки О, которые равны друг другу. В таком случае:
\(AO = OD\)
Из вышесказанного следует, что:
\(\angle ADO = \angle OAD = 28^{\circ}\)
В результате:
\(\angle AOD = 180^{\circ} - 2\cdot 28^{\circ} = 124^{\circ}\)
Ответ: \(124^{\circ}.\)
С помощью точки О сторона ВС, которая принадлежит прямоугольнику ABCD, поделена на отрезки 7 и 1. Точка О удалена от стороны AD на 3. Необходимо вычислить, какой величиной обладает периметр данного прямоугольника.
Решение
Прежде, чем искать периметр, заметим, что расстояние, на которое удалена точка О от стороны AD, аналогично длинам смежных сторон к AD. В таком случае:
\(P_{ABCD} = 2\cdot(7 + 1 + 3) = 22\)
Ответ: 22.
Дан некий прямоугольник \(ABCD\) с диагональю \(AC = 2\cdot CD\). Требуется вычислить разность \(\angle BAC - \angle CAD\).
Решение
Заметим, что треугольник \(ACD\) является прямоугольным. Кроме того, катет этого треугольника соответствует половине гипотенузы, то есть является противолежащим для угла в \(30^{\circ}\). Таким образом:
\(\angle CAD = 30^{\circ}. \angle BAC = 90^{\circ} - \angle CAD = 60^{\circ}\)
В результате:
\(\angle BAC - \angle CAD = 60^{\circ} - 30^{\circ} = 30^{\circ}\)
Ответ: \(30^{\circ}\).
Имеется некий прямоугольник \(ABCD\) с периметром, равным 26, и площадью, соответствующей 40. Необходимо определить, чему равна разность максимальной и минимальной сторон данного прямоугольника.
Решение
Зная, что прямоугольник представляет собой частный случай параллелограмма, сделаем вывод о равенстве его противолежащих сторон. Введем обозначение для длины фигуры (а), выразим ширину фигуры, как (b). В результате, получим:
\( a\cdot b = 40, a + b + a + b = 2(a + b) = 26\)
Таким образом:
\(b = 13 – a\)
\(a \cdot (13 - a) = 40\)
Запишем равносильное выражение:
\(a^2 - 13a + 40 = 0\)
Определим дискриминант:
\(D = 13^2 - 4\cdot 40 = 9 = 3^2\)
Найдем корни:
\(a_1 = 0,5(13 + 3) = 8\)
\(a_2 = 0,5(13 - 3) = 5\)
В первом случае \(b = 8\). С другой стороны, \(a \geq b\). Исключим первый корень. Значит, решениями являются:
\(a = 8\)
\(b = 5\)
Вычислим разность:
\(8 - 5 = 3\)
Ответ: 3.
Отношение периметра прямоугольника \(ABCD\) к периметру треугольника \(АВС\) равно 7:6. Необходимо вычислить, чему равен периметр \(ABCD\) при \(BD = 10\).
Решение
\(P_{\triangle ABC} = AB + BC + AC, P_{ABCD} = 2\cdot(AB + BC) \Rightarrow 2\cdot P_{\triangle ABC} - P_{ABCD} = 2\cdot AC = 2\cdot BD = 20\)
Заметим, что:
\(2\cdot P_{\triangle ABC} - P_{ABCD} = 2\cdot 6\cdot x - 7\cdot x = 5\cdot x \Rightarrow 5\cdot x = 20 \Rightarrow x = 4\)
В результате:
\(P_{ABCD} = 7\cdot x = 28\)
Ответ: 28.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так