Как найти площадь круга: формулы, примеры решения задач
Что такое круг
Кругом называют в геометрии фигуру на плоскости, которая составлена точками, равноудаленными от какой-то точки, выбранной в качестве центральной.
Источник: ru.wikipedia.org
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Согласно еще одному распространенному понятию круг представляет собой фрагмент, расположенный в рамках какой-то плоскости, ограниченный окружностью.
Что такое площадь круга
Площадь любой фигуры, размещенной на плоскости и полностью ей принадлежащей, называют аддитивный численный параметр рассматриваемой фигуры.
Как рассчитать площадь круга: формулы
Существует несколько соотношений для вычисления параметра, который называется площадью круга. Выбрать ту или иную формулу можно на основе известной характеристики геометрической фигуры. К примеру, при решении задач по геометрии, как правило, по условию дается величина радиуса или диаметра круга. Запишем соответствующие уравнения:
\(S=\pi R^2\)
Исходя из того, что радиус круга определяется, как половина его диаметра, можно интерпретировать записанное соотношение и представить его в следующем формате:
\(S=\pi (\frac{D}{2})^2 = \pi \frac{D^2}{4}\)
Источник: shkolkovo.net
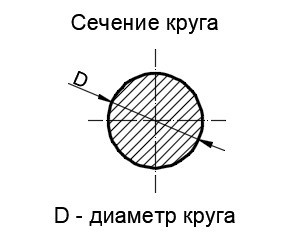
Площадь сечения круга
Сечение круга является рисунком геометрической фигуры, который сформирован путем рассечения круга с помощью плоскости в поперечном направлении.
Источник: www.center-pss.ru
Заметим, что сечение круга также имеет форму круга, то есть представляет собой какую-то часть плоскости, границы которого являются окружностью. В связи с этим понятием целесообразно сделать вывод формулы, которая пригодиться, чтобы вычислить площадь кругового сечения:
\(S= \pi \frac{D^2}{4}\)
Примеры решения задач
Задан некоторый круг. Пусть его радиус составляет 1,2 см. Требуется вычислить площадь данной геометрической фигуры.3адача 1
Решение
Заметим, что по условию известной характеристикой круга является радиус. Тогда целесообразно воспользоваться следующей формулой, чтобы найти, чему равна искомая площадь:
\(S=\pi R^2\)
Путем подстановки численных значений, которые известны по условию задачи, выполним вычисления. Заметим, что в процессе расчетов число \(\pi\) принято принимать за 3,14:
\(S=\pi R^2 = 3,14\cdot 1,2^2 = 3,14 \cdot 1,44 = 4,5216 см^2\)
Важно отметить, что площадь всегда измеряется в единицах, возведенных во вторую степень. По этой причине здесь указан ответ в квадратных сантиметрах.
Ответ: \(4,5216 см^2\)
Задан круг, площадь которого составляет \(1,1304 см^2\). Необходимо найти величину радиуса такой геометрической фигуры.
Решение
В данном случае также пригодится формула для вычисления площади геометрической фигуры, имеющей форму круга:
\(S=\pi R^2\)
Выразим из имеющегося справедливого соотношения радиус, который требуется посчитать по условиям задания. Получим следующее равенство:
\(R = \sqrt{\frac{S}{\pi}}\)
Путем подстановки числовых значений получим искомый результат:
\(R = \sqrt{\frac{S}{\pi}} = \sqrt{\frac{1,1304}{3,14}} = \sqrt{0,36} = 0,6 см\)
Ответ: 0,6 см
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так