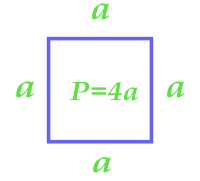Что нужно знать о площади квадрата — основные сведения
Что такое площадь
Площадь является математической величиной, с помощью которой измеряют размер поверхности.
Площадь обозначают, используя математический знак S.
Перечислим популярные единицы измерения площади, которые часто встречаются в задачах:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- квадратный метр \((м^{2})\);
- сантиметр в квадрате \((см^{2})\);
- квадратный миллиметр \((мм^{2})\);
- километр в квадрате \((км^{2})\);
- ар (а);
- гектар (га).
Такая величина, как площадь характеризуется следующими свойствами:
- положительность (при вычислении площади какой-либо фигуры или поверхности получается в любом случае число со знаком плюс, величина не может иметь отрицательное значение);
- нормировка (для определения площади предусмотрены стандартизированные единицы измерения);
- если геометрические фигуры идентичны, то такие фигуры обладают равными площадями;
- площадь совокупности пары фигур без учета единых точек, расположенных во внутреннем пространстве, соответствует сумме площадей.
Формулы для вычисления площади квадрата
Квадратом называют геометрическую фигуру, сформированную с помощью равных по длине отрезков в виде сторон, соединенных в определенной последовательности, противолежащие стороны в которой параллельны парами, а угол между какими-либо двумя смежными сторонами составляет 90 градусов.
Площадь квадрата является числовым параметром, который определяет размер плоскости, ограниченной данной геометрической фигурой.
Существуют разные соотношения для вычисления площади квадрата. Выбор тот или иной формулы обусловлен наличием какой-либо исходной информации. Рассмотрим наиболее часто применяемые уравнения для решения примеров и доказательства различных теорем.
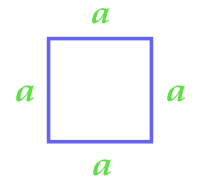
Формула, по которой можно высчитать площадь квадрата с учетом его стороны:
\(S = a^2\)
Здесь а обозначает сторону квадрата.
Площадь квадрата можно находить, если известна его диагональ:
\(S = \frac{d^2}{2},\)
где d является диагональю квадрата.
При известной величине периметра можно рассчитать площадь квадрата таким образом:
\(S = \frac{P^2}{16}\)
Здесь Р обозначает периметр геометрической фигуры.
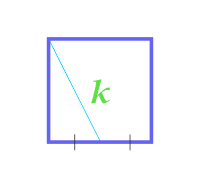
Площадь квадрата также достаточно просто вычислить, если известна длина отрезка, который проведен из вершины геометрической фигуры к середине противолежащей стороны:
\(S = \frac{4 \cdot k^2}{5},\)
При нахождении площади учтем, что k обозначает длину отрезка.
Если в квадрат вписана некая окружность, то его площадь допустимо посчитать через радиус окружности по формуле:
\(S = 4 \cdot r^2\)
Здесь r является радиусом вписанной в квадрат окружности.
Если около квадрата описана окружность, то его площадь вычисляется через радиус этой окружности по формуле:
\(S = 2 \cdot R^2,\)
где R равняется радиусу описанной около квадрата окружности.
Примеры решения задач применением данных формул
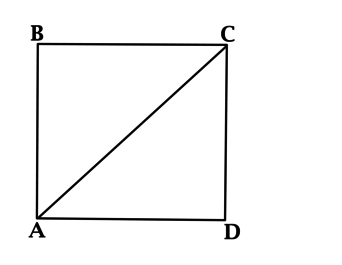
Имеется некий квадрат ABCD со стороной AC, равной 10. Необходимо выполнить расчет площади этого квадрата.
Решение
Заметим, что по определению квадрата:
\(AD = CD\)
Воспользуемся теоремой Пифагора и запишем:
\(AС^2 = AD^2 + CD^2 = 2\cdot AD^2\)
В результате:
\(AD^2 = 50\)
Данное значение справедливо считать площадью квадрата.
Ответ: 50.
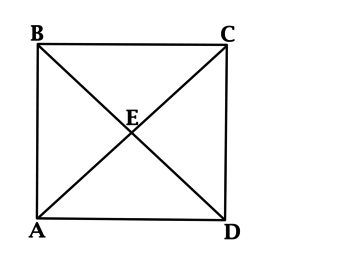
В квадрате ABCD проведены диагонали, которые пересекаются в одной точке. Данная точка удалена от одной из сторон фигуры на 5. Требуется вычислить, чему будет равняться площадь заданного квадрата.
Решение
Обозначим точку, в которой пересекаются диагонали за Е. Исходя из условия задания:
\(AE = ED\)
В таком случае:
\(\angle DAE = \angle EDA\)
Зная, что квадрат представляет собой ромб, сделаем вывод о том, что его диагонали делят углы пополам. Тогда:
\(\angle DAE = 0,5 \cdot 90^{\circ} = 45^{\circ}\)
В результате:
\(\angle AED = 180^{\circ} - 45^{\circ} - 45^{\circ} = 90^{\circ}\)
Рассмотрим треугольник ADE. Проведем высоту EF на AD (длина EF является расстоянием от точки E до стороны). Запишем, что:
\(AE = ED\)
Тогда EF можно назвать медианой. С другой стороны, в прямоугольном треугольнике медиана, которая проведена к гипотенузе, соответствует половине гипотенузы. В результате:
\(EF = 0,5\cdot AD\)
Аналогичным образом, другие расстояния от E до сторон квадрата можно вычислить, как половину стороны квадрата:
\(AD = 10\)
В результате:
\(S = 100\)
Ответ: 100.
Нужно вычислить площадь квадрата, сумма диагоналей в котором составляет 4.
Решение
Зная, что диагонали в квадрате обладают равными величинами, вычислим длину одной диагонали:
\(4 \div 2 = 2\)
Вычислим площадь квадрата, как половину произведения диагоналей:
\(\frac{1}{2}\cdot2\cdot2 = 2\)
Ответ: 2.
Периметр некого квадрата составляет 2. Требуется вычислить площадь этой геометрической фигуры.
Решение
Рассчитаем величину стороны квадрата:
\(2 \div 4 = 0,5\)
Вычислим площадь:
\(0,5\cdot0,5 = 0,25 \)
Ответ: 0,25.
Дан квадрат с площадью, равной 1. Нужно вычислить, чему равен периметр этого квадрата.
Решение
Обозначим за х сторону квадрата АВ. Тогда:
\(x^2 = 1 \Rightarrow x = 1\)
Вычислим периметр:
\(4\cdot x = 4\cdot1 = 4\)
Ответ: 4.
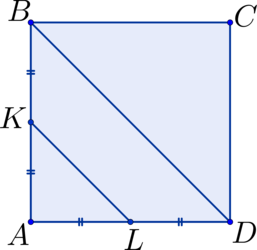
В квадрате ABCD середина стороны AB удалена от середины стороны AD на расстояние, равное 3. Необходимо вычислить площадь квадрата ABCD.
Решение
Отрезок KL соединяет стороны квадрата AB и AD. С другой стороны, этот отрезок является средней линией в \(\triangle ABD\):
\(2\cdot KL = BD\)
\(BD = 6 = AC \Rightarrow S_{ABCD} = \frac{1}{2}\cdot6\cdot6 = 18.\)
Ответ: 18.
Задачи для самостоятельного решения
Треугольник \(\triangle ABD\) обладает площадью, равной 2. Требуется определить периметр квадрата ABCD.
Решение
\( S_{ABCD} = 2\cdot S_{\triangle ABD} = 2\cdot2 = 4\)
Обозначим сторону квадрата за х:
\(x^2 = 4 \Rightarrow x = 2 \Rightarrow P_{ABCD} = 4\cdot x = 4\cdot 2 = 8\)
Ответ: 8.
Задан четырехугольник с площадью, равной 1. Вершины данной фигуры являются серединами сторон квадрата. Требуется вычислить площадь квадрата.
Решение
Исходный четырехугольник представляет собой квадрат, так как его вершины совпадают с серединами сторон квадрата. Диагонали второго квадрата равны сторонам первого квадрата. Запишем следующее:
\(\triangle A'BB'=\triangle B'CC'=\triangle C'DD'=\triangle D'AA'\)
Тогда:
\(A'B'=B'C'=C'D'=D'A'\)
Таким образом, \(A'B'C'D'\) представляет собой ромб. С другой стороны:
\(\angle D'A'A=\angle B'A'B=45^\circ\)
Сделаем следующий вывод:
\(\angle D'A'B'=180^\circ-2\cdot 45^\circ=90^\circ\)
В результате \(A'B'C'D'\) является квадратом. Вычислим площадь:
\(S_{A'B'C'D'}=\frac12 A'C'^2=1 \Rightarrow A'C'^2=2\)
Заметим, что:
\(A'C'=AD\)
Таким образом:
\(S_{ABCD}=AD^2=2\)
Ответ: 2.
Вершины некого четырехугольника являются серединами сторон квадрата. Периметр этого четырехугольника составляет \(4\sqrt2\). Требуется вычислить периметр квадрата.
Решение
Рассматриваемый четырехугольник по условию задачи также является квадратом, так как его вершины соответствуют серединам сторон квадрата. Найдем сторону внутреннего квадрата:
\(4\sqrt2 : 4 = \sqrt2\)
Полученная сторона представляет собой среднюю линию треугольника, образованного с помощью соответствующей диагонали. Таким образом, диагональ внешнего квадрата равна \(2\sqrt2\). Сторона внешнего квадрата при этом составит 2. Вычислим периметр:
\(2\cdot4 = 8\)
Ответ: 8.
На рисунке изображены треугольник и квадрат. Периметр \(\triangle ABD\) составляет \(16 + 8\sqrt2\). Требуется вычислить периметр квадрата \(ABCD\).
Решение
Обозначим за х сторону квадрата. Тогда его диагональ \(\sqrt 2 x\). В результате:
\(P_{\triangle ABD} = x + x + \sqrt 2 x = x\cdot(2+\sqrt2) = 16 + 8\sqrt2 = 8\cdot(2 + \sqrt2) \Rightarrow x = 8 \Rightarrow P_{ABCD} = 4\cdot x = 4\cdot8 = 32\)
Ответ: 32.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так