Что нужно знать о периметре треугольников — основные сведения
Что такое периметр треугольника
Треугольником называют многоугольник, имеющий три вершины и три ребра, соединяющих вершины.
Размер треугольника, как и любой плоской геометрической фигуры, можно описать с помощью таких величин, как площадь и периметр.
Периметром треугольника называют сумму длин его ребер (сторон).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Принято следующее обозначение периметра: заглавная латинская буква P. Периметр измеряется в линейных единицах измерения (метры, сантиметры и т.д.).
Рассмотрим известные способы вычисления периметра для различных видов треугольников.
Периметр разностороннего треугольника
К разносторонним относятся треугольники, которые не являются равносторонними, равнобедренными или прямоугольными.
Иногда для подобных треугольников используют определение «произвольный».
Периметр разностороннего треугольника можно высчитать по:
- по трем сторонам;
- по средним линиям;
- по двум ребрам и углу между ними;
- по радиусу вписанной в треугольник окружности.
Укажем формулы для каждого из приведенных способов.
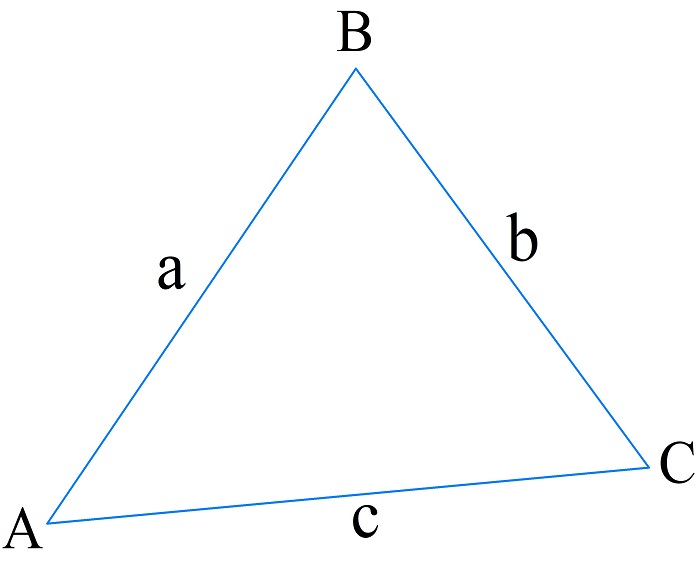
Вычисление периметра по трем сторонам
В этом случае необходимо знать длины всех ребер.
\(P=a+b+c\)
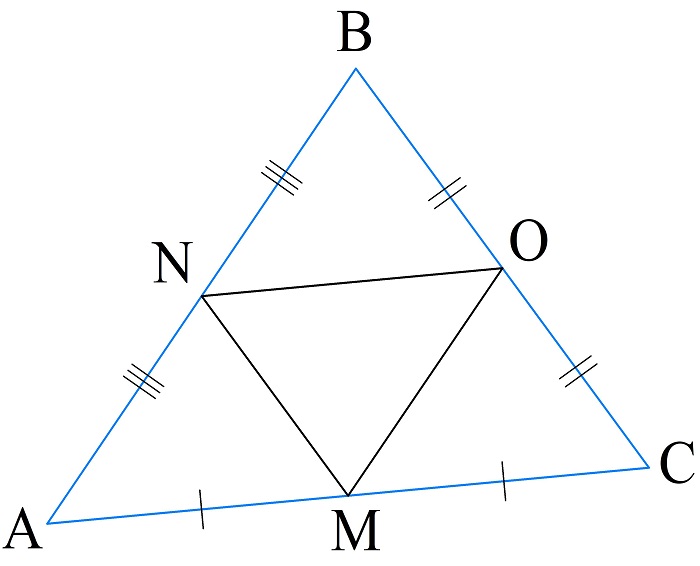
Вычисление периметра по средним линиям
Средняя линия — линия, параллельная одной из сторон треугольника и равная половине ее длины. Значит, периметр треугольника, построенного по средним линиям данного, вдвое меньше периметра данного треугольника.
\(P_{\bigtriangleup ABC}=2\cdot P_{\bigtriangleup MNO}=2\cdot(MN+NO+OM)\)
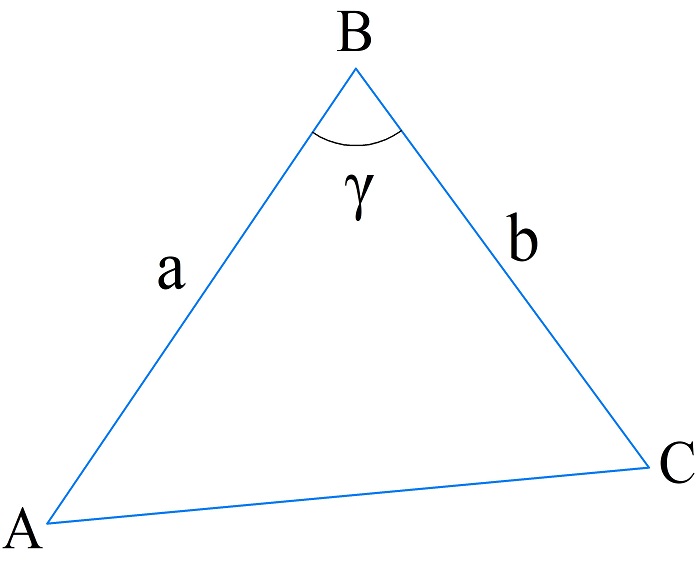
Вычисление периметра по двум сторонам и углу между ними
В этом случае известны только две стороны, а третью находят по теореме косинусов.
Тогда формулу для периметра можно записать в виде:
\(P_{\bigtriangleup ABC}=a+b+\sqrt{a^2+b^2-2ab\cdot\cos\gamma}\)
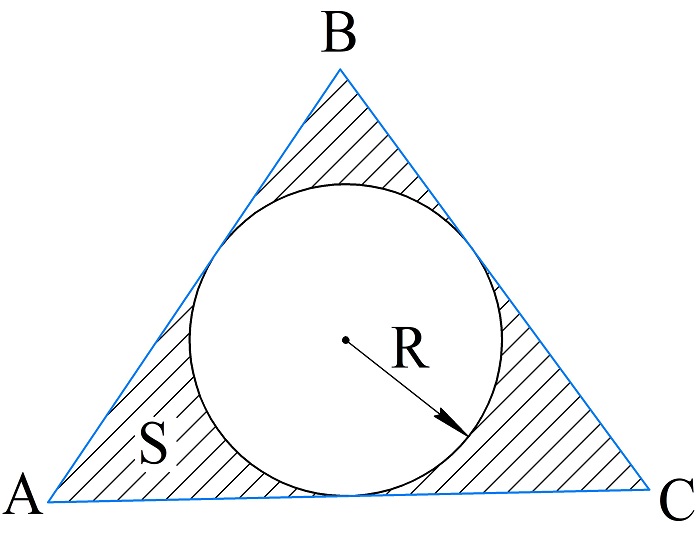
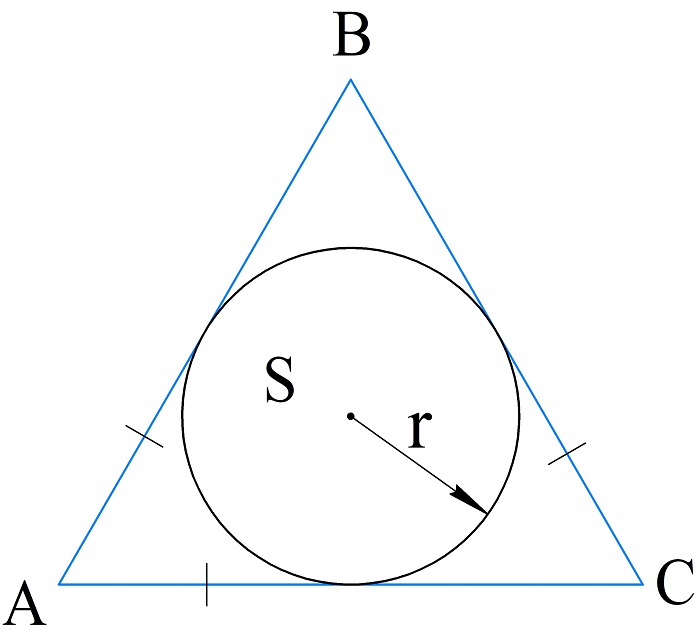
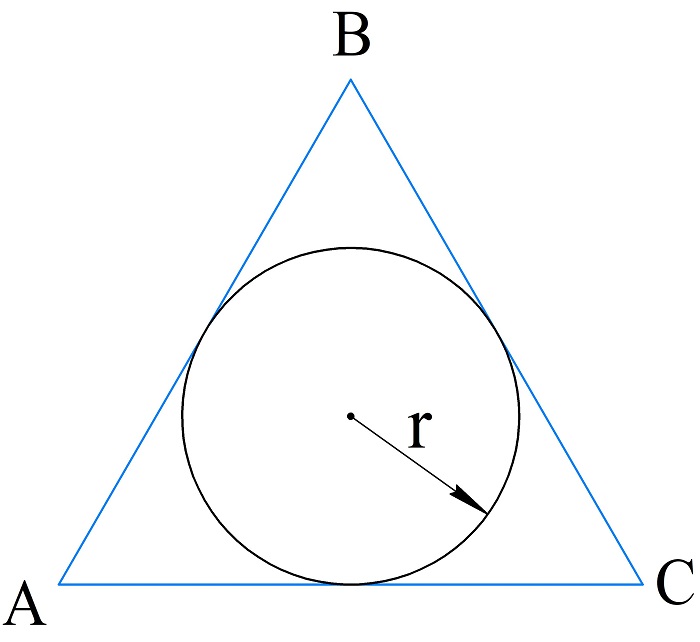
Вычисление периметра по радиусу вписанной окружности
Согласно теореме о вписанной окружности в любой треугольник можно вписать окружность, именно поэтому этот способ применим для произвольных треугольников.
Итак, если известна площадь треугольника и радиус вписанной окружности, то периметр вычисляют по формуле:
\(P_{\bigtriangleup ABC}=\frac{2S_{\bigtriangleup ABC}}R\)
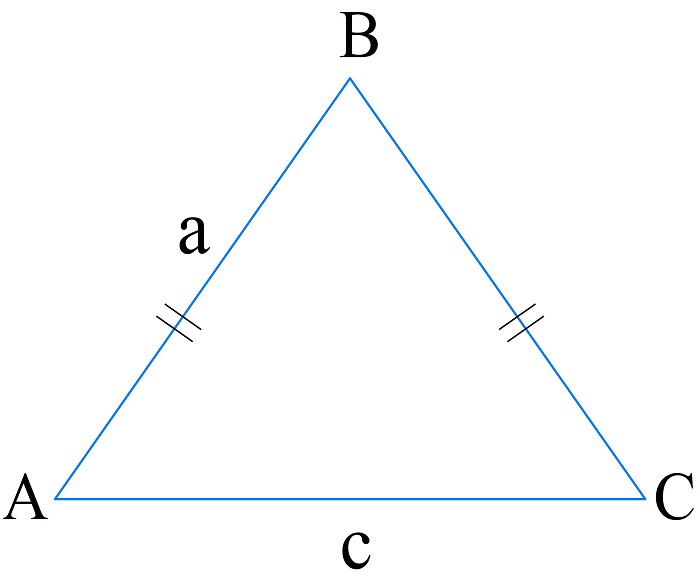
Вычисление периметра равнобедренного треугольника
Равнобедренным называют треугольник, у которого две стороны равны, и углы, образованные этими сторонами и третьей (основанием), также равны между собой.
Как правило, периметр равнобедренного треугольника ищут по:
- одной из боковых сторон и основанию;
- основанию и высоте;
- одной из боковых сторон и высоте.
Вычисление периметра по боковой стороне и основанию
В равнобедренном треугольнике боковые стороны равны, тогда:
\(P_{\bigtriangleup ABC}=2a+c\)
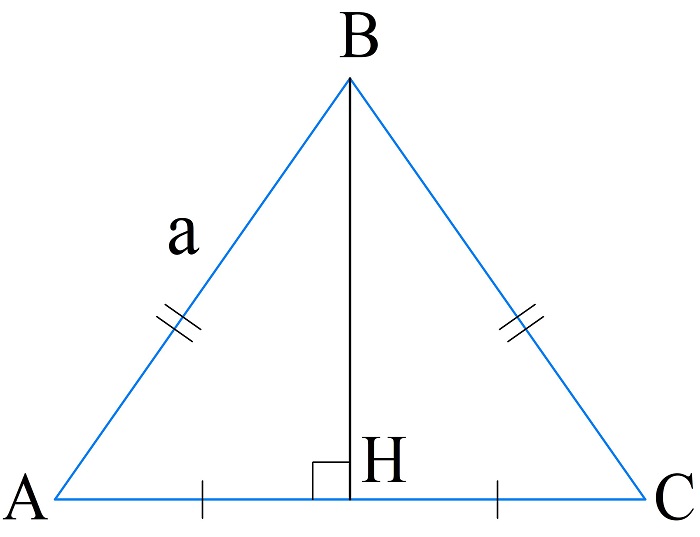
Вычисление периметра по основанию и высоте
В равнобедренном треугольнике высота, проведенная к основанию является медианой, тогда неизвестную боковую сторону можно посчитать по теореме Пифагора. Периметр треугольника:
\(P_{\bigtriangleup ABC}=2\cdot\sqrt{h^2+\frac{c^2}4}+c=\sqrt{4h^2+c^2}+c\)
Вычисление периметра по боковой стороне и высоте
Этот способ, как и предыдущий, основан на вычислении неизвестной стороны по теореме Пифагора. Периметр можно рассчитать по формуле:
\(P_{\bigtriangleup ABC}=2\cdot\sqrt{a^2-h^2}+2a\)
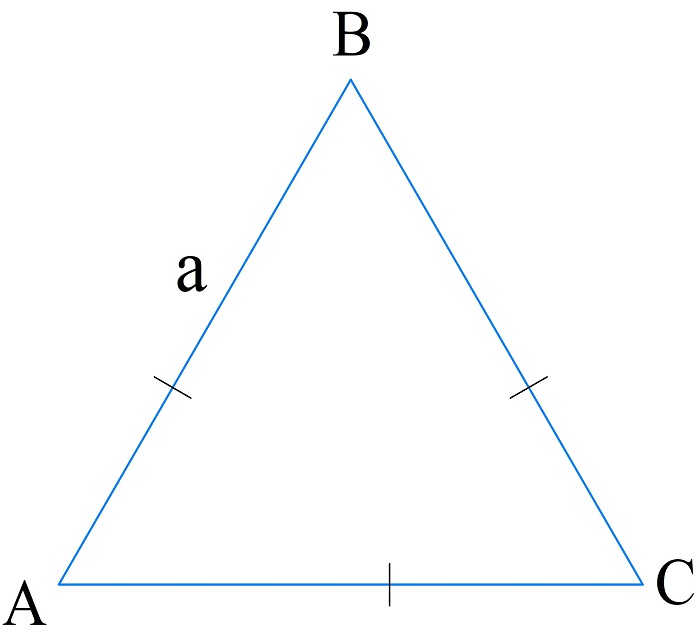
Как найти периметр равностороннего треугольника
Равносторонним называется такой треугольник, у которого все стороны равны между собой, а каждый из углов равен \(60^0\).
Периметр равностороннего треугольника находят по:
- стороне;
- высоте;
- площади вписанной окружности.
Вычисление периметра по стороне
Так как все стороны данного вида треугольника равны, то периметр вычисляется по формуле:
\(P_{\bigtriangleup ABC}=3a\)
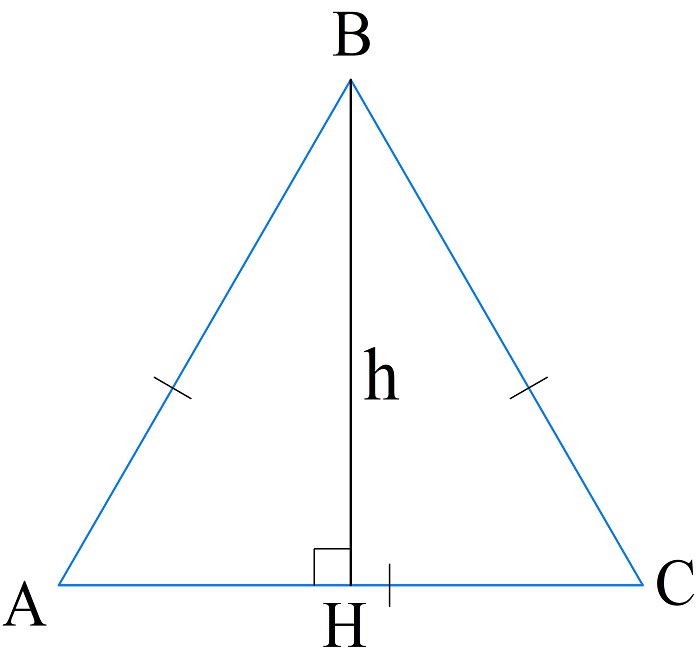
Вычисление периметра по высоте
Из прямоугольного треугольника ABH получают соотношение высоты и стороны треугольника:
\(h=\frac{\sqrt3}2a\)
Периметр через высоту находят по формуле:
\(P_{\bigtriangleup ABC}=3a=3\cdot\frac2{\sqrt3}h=\frac6{\sqrt3}h\)
Вычисление периметра по площади вписанной окружности
Площадь вписанной в равносторонний треугольник окружности связана со стороной треугольника соотношением:
\(S=\frac{a^2\cdot\sqrt3}4\)
Из указанного соотношения выражают сторону и вычисляют периметр по формуле:
\(P_{\bigtriangleup ABC}=3a=3\cdot\sqrt{\frac{4S}{\sqrt3}}=6\sqrt{\frac S{\sqrt3}}\)
Нахождение периметра прямоугольного треугольника
Прямоугольным треугольником называют треугольник, две стороны которого (катеты) образуют прямой угол.
Периметр прямоугольного треугольника вычисляют по:
- катету и гипотенузе;
- двум катетам;
- катету и прилежащему к нему углу.
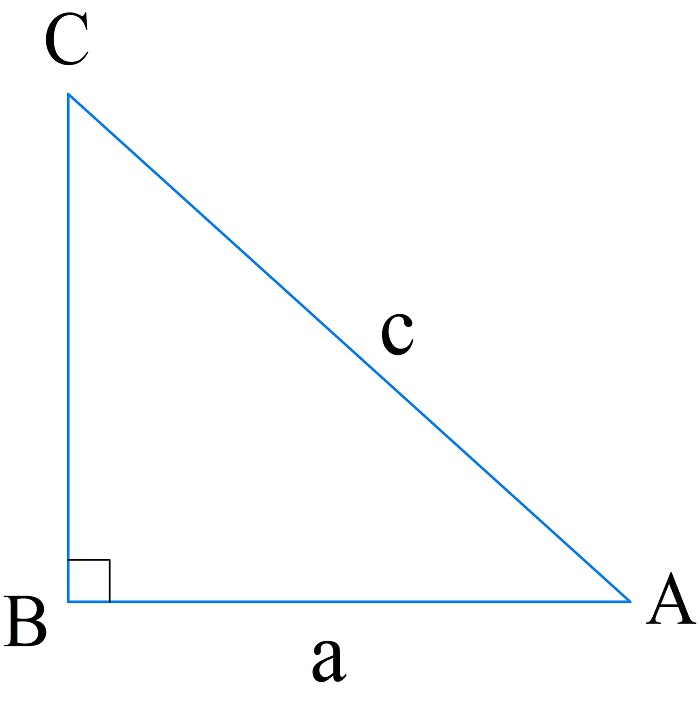
Вычисление периметра по катету и гипотенузе
Второй катет вычисляют по теореме Пифагора, затем находят периметр по формуле:
\(P_{\bigtriangleup ABC}=\sqrt{c^2-a^2}+a+c\)
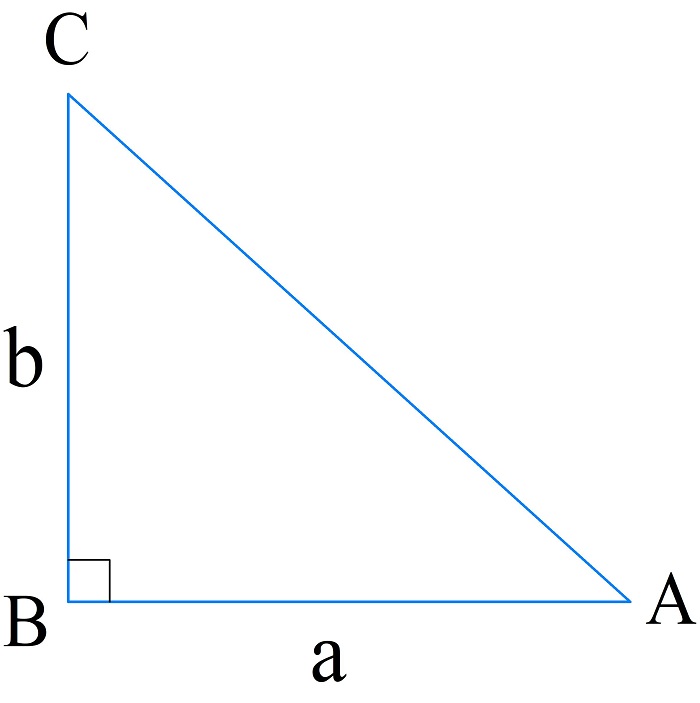
Вычисление периметра по двум катетам
Способ аналогичен предыдущему, гипотенузу рассчитывают по теореме Пифагора, затем определяют периметр:
\(P_{\bigtriangleup ABC}=\sqrt{b^2+a^2}+a+b\)
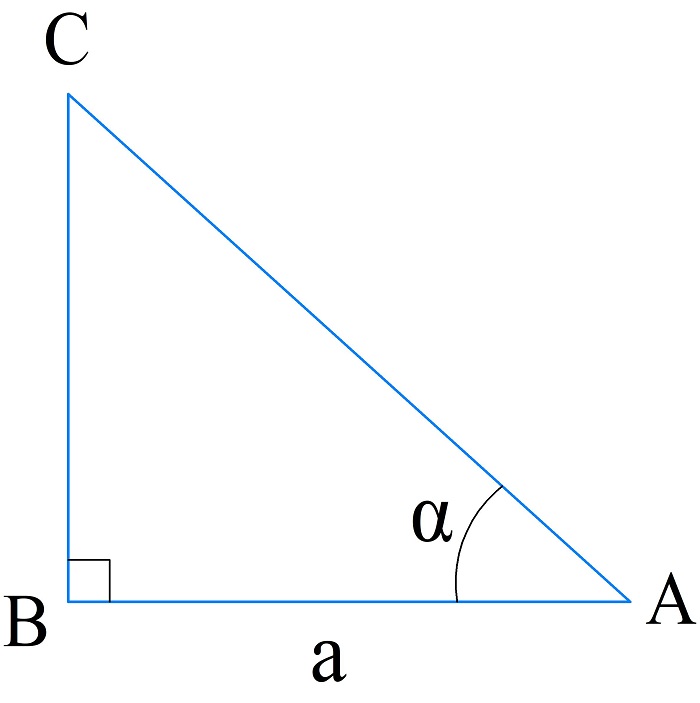
Вычисление периметра по катету и прилежащему к нему углу
В этом случае гипотенузу находят через отношение известного катета к косинусу угла. Второй катет вычисляют по теореме Пифагора. Тогда периметр:
\(P_{\bigtriangleup ABC}=\sqrt{\frac{a^2}{\cos^2\alpha}-a^2}+a+\frac a{\cos\alpha}=a\cdot\left(1+\frac1{\cos\alpha}+\sqrt{\frac1{\cos^2\alpha}-1}\right)\)
Примеры решения задач
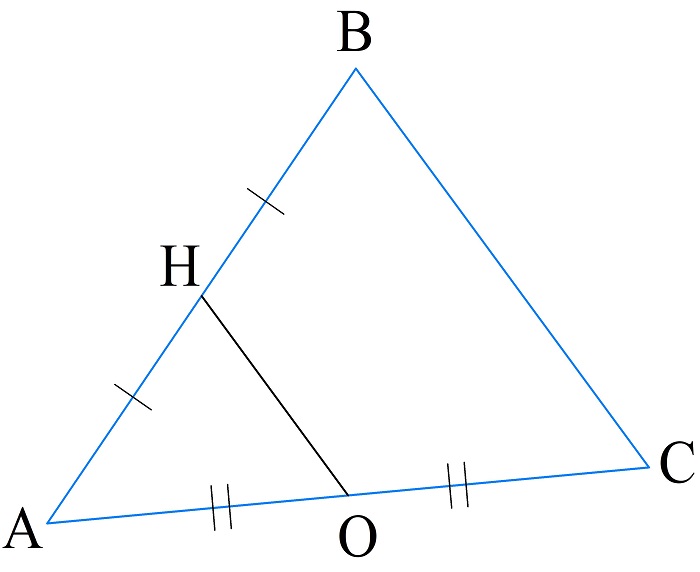
В произвольном треугольнике ABC проведена средняя линия OH. Известно, что AO=2 см, AB=8 см, а периметр ABC равен 20 см. Найти длину средней линии.
Решение
Периметр треугольника OAH в два раза меньше периметра ABC, то есть равен 10 см. Отрезки AH и HB равны между собой и равны 4 см.
Тогда длину средней линии определим как:
\(OH=P_{\bigtriangleup OAH}-AH-AO=10-4-2=4\;см\)
Ответ: 4 см.
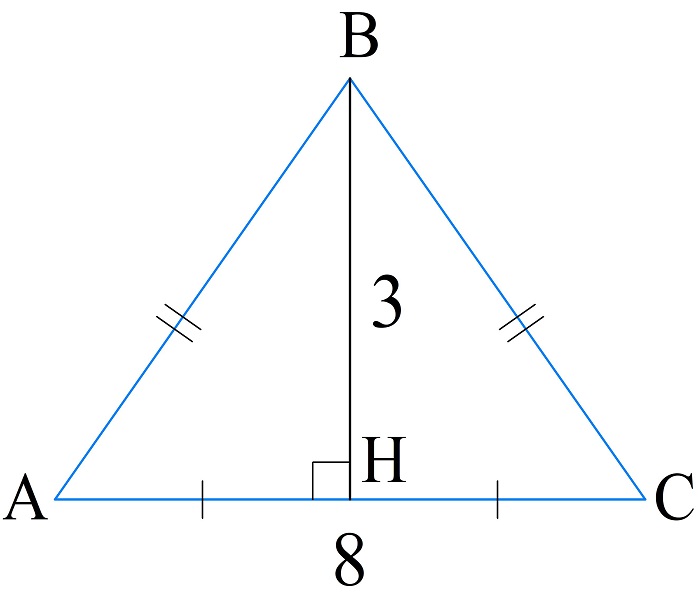
В равнобедренном треугольнике ABC с основанием AC=8 см проведена высота BH=3 см. Вычислить периметр треугольника.
Решение
Вычислим боковую сторону треугольника по теореме Пифагора:
\(AB=\sqrt{BH^2+AH^2}=\sqrt{3^2+\left(\frac82\right)^2}=5\;см\)
Тогда периметр:
\(P_{\bigtriangleup ABC}=AC+2\cdot AB=8+10=18\;см\)
Ответ: 18 см.
В равносторонний треугольник вписана окружность радиусом \(r=2\cdot\sqrt[4]3\;см\). Найти периметр треугольника.
Решение
Вычислим площадь окружности:
\(S=\mathrm\pi\cdot\mathrm r^2=\mathrm\pi\cdot{(2\cdot\sqrt[4]3\;)}^2=4\mathrm\pi\cdot\sqrt3\;\mathrm{см}^2\)
Тогда периметр:
\(P_{\bigtriangleup ABC}=6\cdot\sqrt{\frac{4\mathrm\pi\sqrt3}{\sqrt3}}=12\cdot\sqrt{\mathrm\pi}\;см\)
Ответ: \(12\cdot\sqrt{\mathrm\pi}\;см.\)
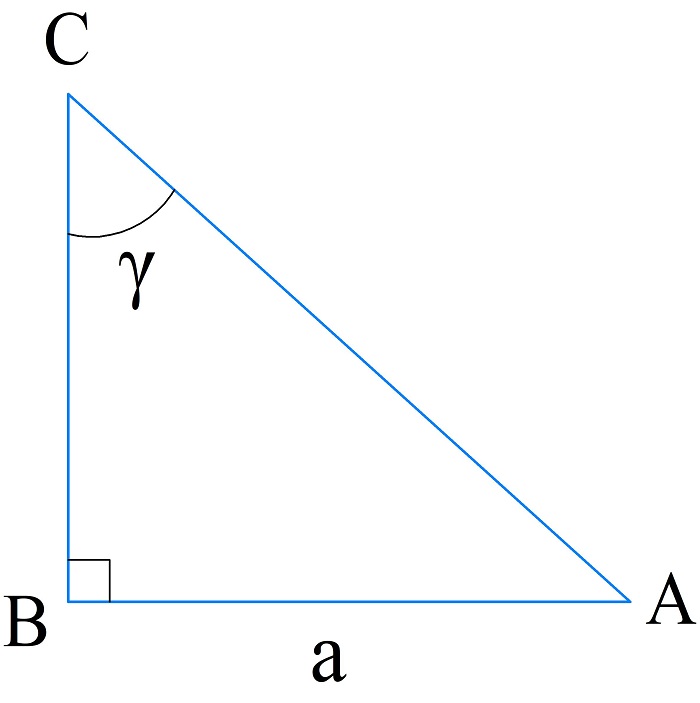
Выведите формулу для расчета периметра прямоугольного треугольника по катету и противолежащему углу.
Решение
Гипотенузу найдем из определения синуса угла:
\(\sin\gamma=\frac a{AC}\;\Rightarrow\;AC=\frac a{\sin\gamma}\)
По теореме Пифагора вычислим второй катет:
\(BC=\sqrt{AC^2-AB^2}=\sqrt{\frac{a^2}{\sin^2\gamma}-a^2}=a\sqrt{\frac1{\sin^2\gamma}-1}\)
Периметр:
\(P_{\bigtriangleup ABC}=a+\frac a{\sin\gamma}+a\sqrt{\frac1{\sin^2\gamma}-1}=a\left(1+\frac1{\sin\gamma}+\sqrt{\frac1{\sin^2\gamma}-1}\right)\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так