что нужно знать о периметре трапеций — основные сведения
Трапеция. Основные понятия и определения
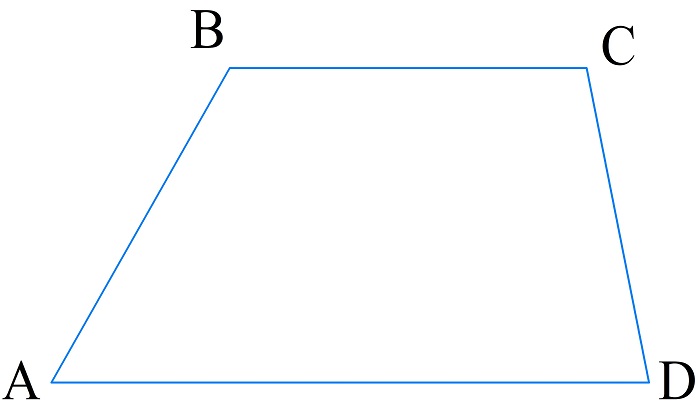
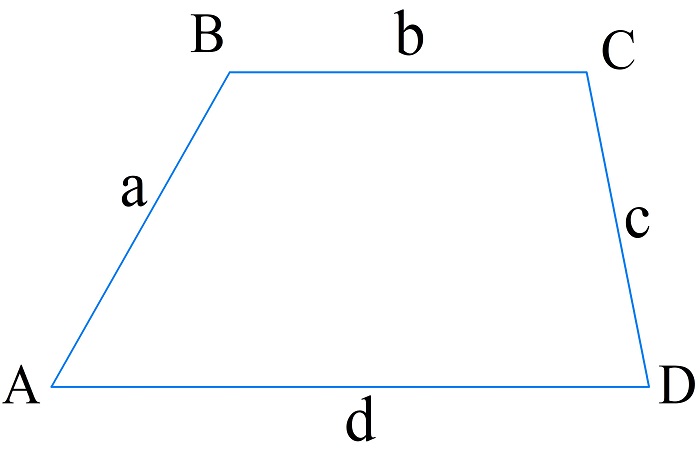
Трапеция — четырехугольник, две противоположные стороны которого параллельны между собой.
Две параллельные стороны называют основаниями (верхним и нижним), а непараллельные — боковыми сторонами.
Выделяют особый вид трапеции — равнобедренную или равнобокую.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
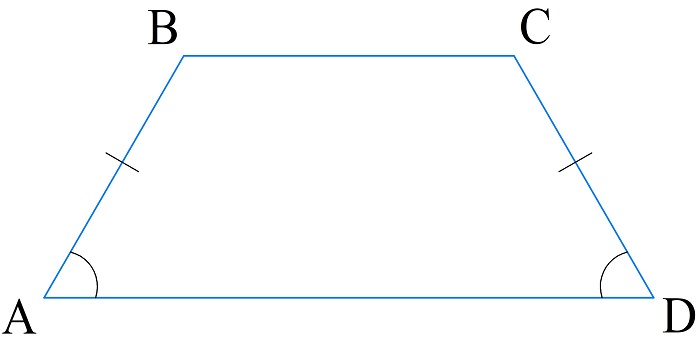
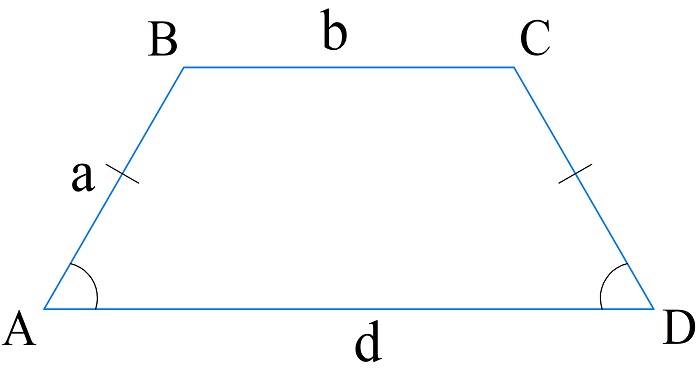
Равнобедренной называют трапецию, боковые ребра которой равны, и углы при нижнем основании равны между собой.
Допускается применять как термин «равнобокая», так и «равнобедренная», так как эти понятия аналогичны друг другу.
В равнобедренную трапецию всегда можно вписать и описать около нее окружность.
Рассмотрим еще несколько основных понятий.
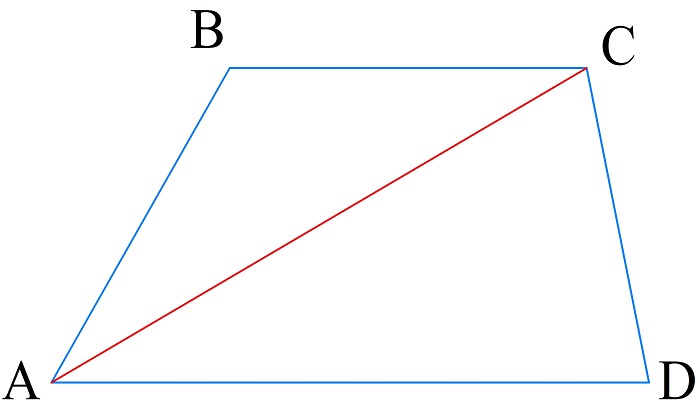
Диагональ трапеции — линия, соединяющая две ее несмежные вершины.
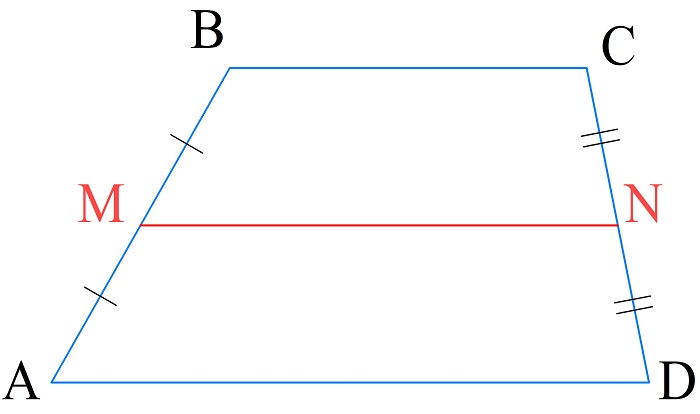
Средняя линия — отрезок, параллельный основаниям трапеции и равный их полу сумме.
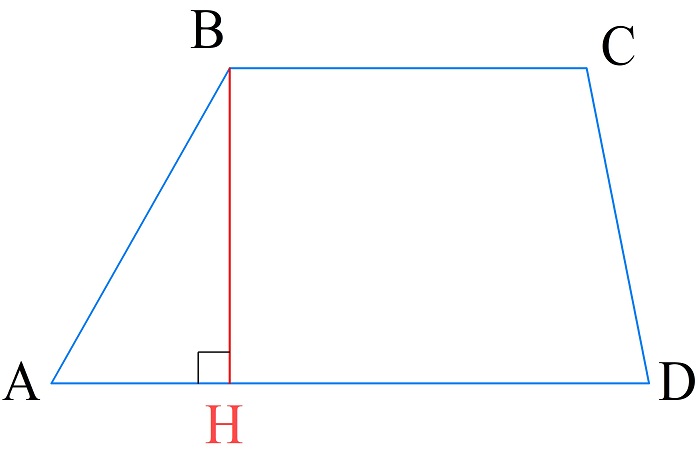
Высота — перпендикуляр, проведенный из любой точки одного из оснований трапеции ко второму ее основанию.
К количественным характеристикам трапеции относят:
- площадь;
- периметр.
В данной статье рассмотрим способы, с помощью которых можно найти периметр трапеции.
Периметр трапеции — величина, равная сумме длин всех четырех ребер фигуры.
Периметр обозначают в виде большой буквы P.
Способы нахождения периметра
Периметр фигуры можно найти, если:
- В произвольной трапеции известны длины всех четырех ребер. Это самый простой способ, однако для его применения необходимо знать длину каждого из ребер, а это не всегда возможно.
- В равнобедренной трапеции известны длина боковой стороны и длины оснований.
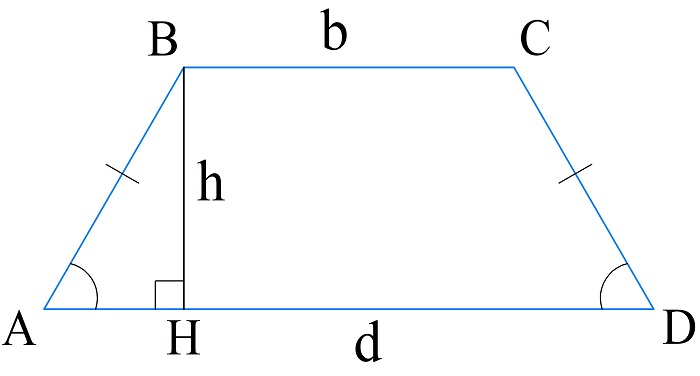
- В равнобедренной трапеции известна длина высоты, проведенной из вершины меньшего из оснований, и длины оснований. Такая высота делит большее основание на два отрезка. Больший из получившихся отрезков при этом равен полу сумме оснований или средней линии. Затем используют теорему Пифагора для прямоугольного треугольника и вычисляют длину бокового ребра.
- Известна длина средней линии произвольной трапеции и длины ее боковых ребер.
Формулы для вычисления периметра к каждому из способов
Приведем формулы вычисления периметра для каждого из указанных способов.
Вычисление периметра по четырем сторонам
\(P_{ABCD}=a+b+c+d\)
Вычисление периметра равнобокой трапеции по основаниям и боковой стороне
\(P_{ABCD}=2a+b+d\)
Вычисление периметра равнобокой трапеции по высоте и основаниям
Сначала определим длину отрезка AH и бокового ребра AB.
\(AH=AD-HD=d-\frac{b+d}2=\frac{d-b}2\)
\(AB=\sqrt{AH^2+BH^2}=\sqrt{\frac{\left(d-b\right)^2}4+h^2}\)
Периметр вычислим по формуле:
\(P_{ABCD}=2AB+AD+BC=2\cdot\sqrt{\frac{\left(d-b\right)^2}2+h^2}+d+b=\sqrt{\left(d-b\right)^2+4h^2}+d+b\)
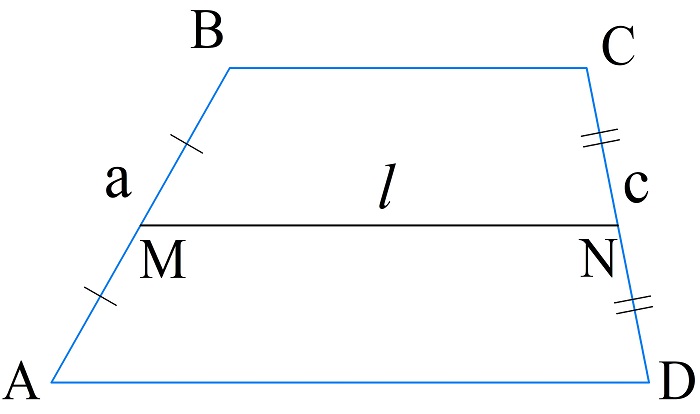
Вычисление периметра трапеции по средней линии
\(P_{ABCD}=AB+CD+2\left(\frac{BC+AD}2\right)=a+c+2l\)
Примеры задач по теме и их решения
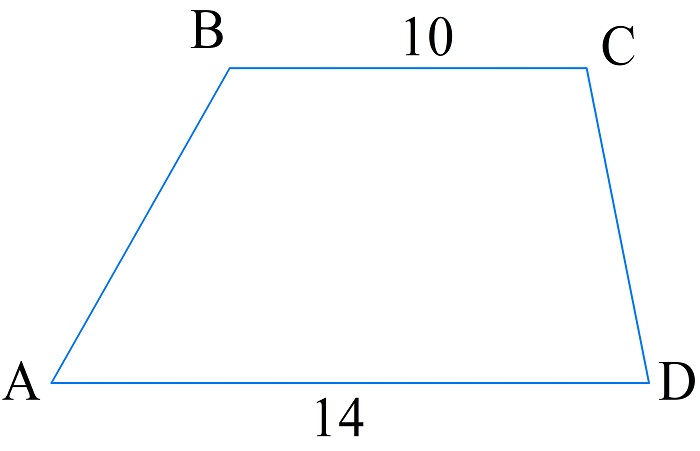
Периметр трапеции ABCD равен 40 см. Известно, что основания равны 10 см и 14 см. А одно боковое ребро больше второго на 2 см. Найдите длины боковых сторон трапеции.
Решение
Обозначим неизвестную длину меньшего ребра AB за x, тогда CD=x+2.
Из формулы для нахождения периметра получим уравнение с неизвестной переменной x:
\(P_{ABCD}=AB+BC+CD+AD=10+14+x+(x+2)=2x+26=40\)
Решив уравнение, получим, что AB=7 см, а CD=9 см.
Ответ: 7 см и 9 см.
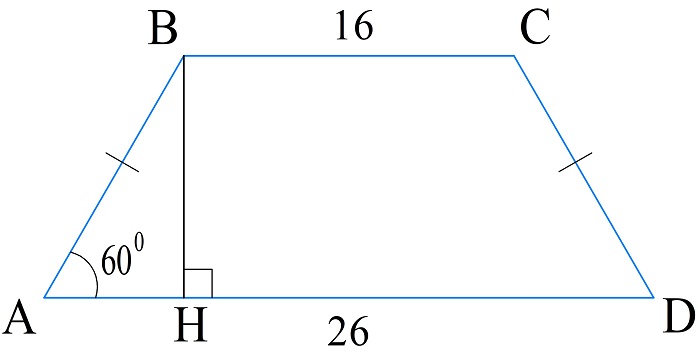
Дана равнобедренная трапеция ABCD с основаниями 26 см и 16 см. Известно, что угол при большем основании равен 60 градусам. Найти периметр трапеции.
Решение
В трапеции проведем высоту BH, получим прямоугольный треугольник ABH. Длину отрезка AH найдем как половину разности оснований:
\(AH=\frac{AD-BC}2=5\;см\)
По определению косинуса угла:
\(\cos\angle A=\frac{AH}{AB}\;\;\Rightarrow\;AB=\frac{AH}{\cos\angle A}=\frac5{\cos60^0}=10\;см\)
Периметр равнобокой трапеции найдем по основаниям и боковой стороне:
\(P_{ABCD}=2AB+BC+AD=20+16+26=62\;см\)
Ответ: 62 см.
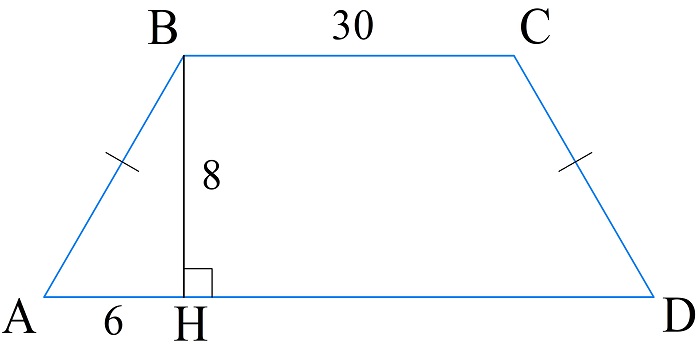
Известно, что у трапеции ABCD ребра AB и CD равны и расположены под одинаковыми углами к AD, при этом BC=30 см. Из вершины B проведена высота BH=8 см такая, что отрезок AH=6 см. Найти периметр трапеции.
Решение
Чтобы найти периметр, необходимо вычислить длину большего основания. Трапеция по условию задачи является равнобедренной, тогда отрезок AH равен половине разности оснований:
\(AH=\frac{AD-BC}2\;\Rightarrow\;AD=2\cdot AH+BC=12+30=42\;см\)
Теперь вычислим периметр по высоте и основаниям:
\(P_{ABCD}=\sqrt{\left(AD-BC\right)^2+4BH^2}+AD+BC=\sqrt{\left(42-30\right)^2+4\cdot8^2}+42+30=92\;см\)
Ответ: 92 см.
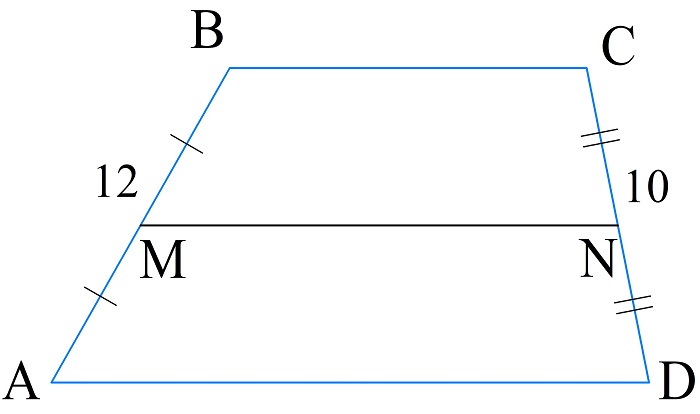
Боковые ребра трапеции ABCD равны 12 см и 10 см. Известно, что одно основание больше другого в 2 раза, а периметр трапеции составляет 70 см. Найти длины оснований трапеции.
Решение
Решать задачу будем через среднюю линию – MN. Обозначим меньшее основание BC за x, тогда AD=2x.
Из условия задания известен периметр фигуры, а значит, можно определить длину отрезка MN:
\(P_{ABCD}=AB+CD+2MN=22+2MN=70\;см\)
\(MN=\frac{70-22}2=24\;см\)
Зная, что средняя линия равна полу сумме оснований, запишем и решим относительно переменной x следующее уравнение:
\(MN=\frac{BC+AD}2=\frac{x+2x}2=24\;см\)
\(\begin{array}{c}x+2x=48\;см\\3x=48\;см\\x=16\;см\end{array}\)
Получили, что меньшее основание BC равно 16 см, а большее AD – 32 см.
Ответ: 16 см и 32 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так