Что нужно знать о периметре прямоугольников — основные сведения
- Какую фигуру называют «прямоугольник» и что такое периметр
-
Способы нахождения периметра прямоугольника
- Расчет периметра с учетом знания величин всех или же только двух прилежащих сторон
- Расчет периметра с учетом знания любой стороны, а также площади
- Расчет периметра в условиях знания величины любой стороны, а также диагонали
- Расчет периметра в условиях знания величины одной любой стороны, а также радиуса описанной окружности
- Формулы, которые используются в задачах
- Примеры решения задач
Какую фигуру называют «прямоугольник» и что такое периметр
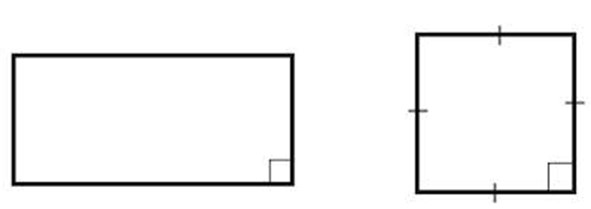
Прямоугольником называют такого вида четырехугольник, характеристиками которого служат две одинаковые по собственной длине стороны.
В то же время, каждый внутренний угол в данной фигуре считается прямым, таким образом равняется \(90^{\circ}\). Получается, что прямоугольник можно считать видом геометрической фигуры, что обладает диадой сторон. Такие геометрические стороны измеряются тождественно, однако в этот же момент являются параллельными друг другу.
Такую фигуру, как прямоугольник, можно считать особым вариантом такой фигуры как параллелограмм. Данная геометрическая фигура представляет собой четырехугольник, в котором противоположные друг другу стороны являются параллельными. Но не у всех параллелограммов существуют схожие характеристики. Сама по себе подобная фигура является соединением четырех отдельных точек. Данные точки носят название вершин. Четыре стороны прямоугольника формируют друг с другом прямые углы в 90 градусов, тогда как внутренняя угловая сумма составляет \(360^{\circ}\).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
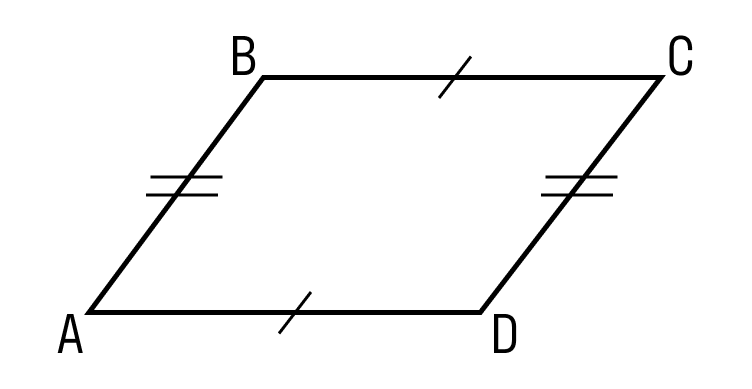
Так выглядит такая геометрическая фигура как параллелограмм:
Такая геометрическая фигура, как квадрат, способна называться особым вариантом прямоугольника.
Специфические характеристики прямоугольника
Существуют следующие характеристики этой фигуры:
- Как известно, прямоугольник можно считать особым случаем параллелограмма, а это значит, что все специфические характеристики параллелограмма можно применять и на эту фигуру.
- Высотой может быть каждая грань прямоугольника.
- Равными можно считать диагонали этой фигуры.
- Диагональ в квадрате эквивалентна сумме прилегающих сторон в квадрате: \(d^{2}=x^{2}+y^{2}\).
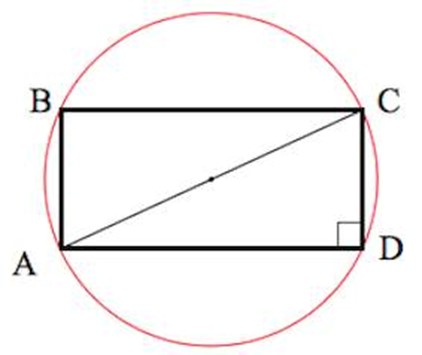
- Можно сделать описание окружности около любого прямоугольника при условии, что диагональ прямоугольника равняется значению диаметра окружности, которая описана.
Так выглядит окружность, которая описана:
Отличительные признаки параллелограмма как геометрической фигуры
Параллелограмм считается прямоугольником в случае, если будет выполнение любое из следующих условий:
- Эквивалентными можно считать диагонали параллелограмма.
- Значения диагоналей параллелограмма в квадрате эквивалентны сумме прилегающих граней в квадрате.
- Эквивалентным (тождественным, равным) можно назвать каждый угол параллелограмма.
- Эквивалентными можно назвать все грани параллелограмма.
- У каждого параллелограмма существует хотя бы один угол в \(90^{\circ}\).
- В случае, если в фигуре XYZD можно выделить треугольники XYD и DZX, тогда их можно считать равнозначными (конгруэнтными).
Конгруэнтность — отношение эквивалентности на большей части геометрических фигур (к примеру, углов, участков, треугольников и так далее).
Площадь прямоугольника
Существует две формулы для нахождения значения площади в такой геометрической фигуре, как прямоугольник:
\(S=xy \) и \(S=\frac{1}{2}d^{2}\sin\alpha\).
Хотя не каждая прямоугольная фигура может считаться квадратом, каждая квадратная фигура может считаться прямоугольной фигурой, в то время как составная фигура может состоять их прямоугольник фигур.
Значение площади, а также стороны прямоугольной фигуры
- Длиной прямоугольной фигуры может считаться метраж самой протяженной диады сторон этой фигуры, шириной прямоугольной фигуры может считаться длина самой наименее протяженной диады сторон этой фигуры.
- Величина площади прямоугольной фигуры эквивалентна итогу умножения ширины прямоугольной фигуры на собственную длину прямоугольной фигуры.
- Значение периметра прямоугольной фигуры эквивалентна удвоенной величине показателей его ширины и длины.
Прямоугольная фигура: диагонали
К диагоналям прямоугольной фигуры можно применять такие условия:
- Диагональные длины в прямоугольной фигуре являются эквивалентными.
- В прямоугольной фигуре диагонали разделяются с помощью места соединения наполовину.
- В прямоугольной фигуре величина длины диагонали способна быть рассчитана в случае применения пифагоровой теоремы, эквивалентна корню в квадрате из величины ширины и длины в квадрате.
Элементы прямоугольной фигуры
Элементы прямоугольной фигуры возможно рассмотреть на предложенном ниже графике:
Посмотрите, на данном графике вершинами являются A, B, C, D; сторонами являются AB, BC, DC, AD, причем AB=DC, а также AD=BC; диагоналями являются AC, DB; внутренними углами являются все прямые углы (90 градусов).
Диагональ прямоугольника
У прямоугольника существуют две диагонали. Точка, в которой пересекаются две диагонали, носит название «центр симметрии» прямоугольника.
Формула для расчета количества диагоналей прямоугольника
\(Nd=\frac{n(n-3)}{2}\)
В данной формуле Nd является количеством диагоналей, n является количеством сторон. Из-за того, что у прямоугольника существует четыре стороны, тогда n=4. Если подставить это значение в формулу выше, тогда количество диагоналей прямоугольника равняется двум. То есть, \(Nd=\frac{4(4-3)}{2}\).
Как можно рассчитать диагональ в прямоугольнике?
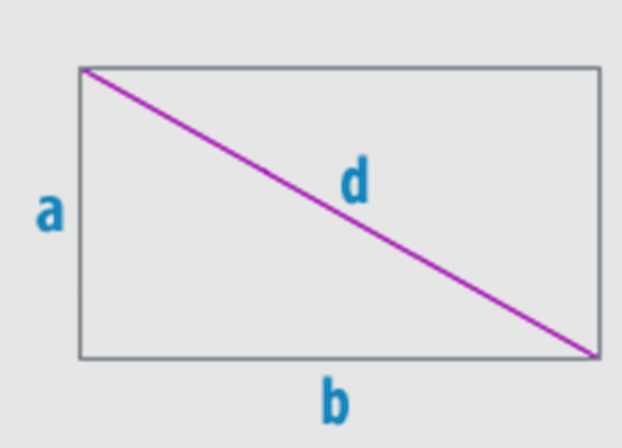
Если рассматривать каждую из диагоналей фигуры, возможно понять, что формируется прямоугольный треугольник. Из-за этого можно говорить, что диагональ (то есть d) является гипотенузой, основание (то есть b (y)), а также высота (то есть a (x)) являются катетами.
Тогда d является длиной диагонали, b является основой прямоугольника, a является высотой прямоугольника. Применим теорему Пифагора для того, чтобы найти диагональ прямоугольника:
\(d^{2}=x^{2}+y^{2}\), из-за этого \(d=\sqrt{y^{2}+x^{2}}\).
Периметр — итог сложения длин всех граней конкретной фигуры. Обычно периметр обозначают при помощи капитальной буквой латинского алфавита P. Очень часто также под P прописывают небольшими буквами латинского алфавита обозначения конкретной фигуры для того, чтобы не сделать ошибок в ходе расчета величин в задачах.
Если длины сторон фигуры задаются разными единицами измерения, тогда невозможно узнать периметр прямоугольника. Из-за этого ради правильного решения нужно перевести абсолютно все сведения к одной единице измерения.
В чем возможно измерить периметр:
- в миллиметрах (сокращенно мм);
- в сантиметрах (сокращенно см);
- в дециметрах (сокращенно дм);
- в метрах (сокращенно м);
- в километрах (сокращенно км).
Также существуют и другие единицы измерения длины.
Способы нахождения периметра прямоугольника
Периметр прямоугольника — это сумма всех четырех сторон, общее расстояние от его внешней границы. Из-за того, что у прямоугольника равные стороны в соотношении два к двум, его периметр будет вдвое больше суммы двух смежных сторон (т.е. a и b). Периметр прямоугольника считается линейной мерой, может быть выражен в линейных единицах измерения, таких как метр, фут, дюйм или ярд.
Приведем простой пример, что такое периметр. Если обойти парковое пространство по его границе, возможно пройти конкретное расстояние. Данное расстояние можно считать значением периметра парка. Для того, чтобы рассчитать периметр каждого прямоугольника, нужно переместиться по границам четырех сторон поля. Нужно начинать считать с определенной точки, которая носит название начальной точки, а заканчивать расчеты после достижения начальной точки.
Расчет периметра с учетом знания величин всех или же только двух прилежащих сторон
Для расчета периметра можно использовать следующие формулы в таком случае:
- При условии, что известны длина всех сторон прямоугольника, нужно просто просчитать сумму данных величин. \(P=x+y+z+d\).
- При условии, что известны только две соседние стороны, необходимо суммировать все стороны, а также помнить сумма на два. \(P=2(x+y)\).
В данных формулах P является искомым периметром, а \(x,y,z,d\) являются сторонами прямоугольника.
Расчет периметра с учетом знания любой стороны, а также площади
В таком случае необходимо использовать такой алгоритм:
- Разделить площадь на длину уже известной стороны.
- Суммировать результат и известную сторону.
- Совершить умножение полученной величины на два.
Можно записать формулу как:
\(P=2(x+\frac{S}{x})\)
В данной формуле P является искомым периметром прямоугольника, x является известной стороной, S является площадью прямоугольника.
Расчет периметра в условиях знания величины любой стороны, а также диагонали
В таком случае необходимо пользоваться таким алгоритмом:
- Рассчитать разность квадратов стороны и диагонали.
- Найти корень, исходя из результатов первого пункта.
- Суммировать итоговое число из второго пункта к известной стороне.
- Совершить умножение результата на два.
\(P=2(x+\sqrt{(d^{2}-x^{2})})\)
В данной формуле P является искомым периметром прямоугольником, x является известной, по условиям задачи, стороной, d является диагональю.
Расчет периметра в условиях знания величины одной любой стороны, а также радиуса описанной окружности
В таком случае необходимо пользоваться таким алгоритмом:
- Совершить умножение квадрата радиуса на четыре.
- Рассчитать разность полученной величины и квадрата известной стороны.
- Рассчитать корень из итогового числа.
- Суммировать конечное число с известной стороной.
- Совершить умножение результата на два
\(P=2(x+\sqrt{(4R^{2}-x^{2})})\)
В данной формуле P является искомым периметром прямоугольника, a является известной стороной, R является радиусом окружности, которая описана вокруг прямоугольника.
Формулы, которые используются в задачах
В задачах на нахождение периметра обычно используются следующие формулы:
- \(P=x+y+z+d\).
- \(P=2(x+y)\).
- \(P=2(x+\frac{S}{x})\).
- \(P=2(x+\sqrt{(d^{2}-x^{2})})\).
- \(P=2(x+\sqrt{(4R^{2}-x^{2})})\).
Примеры решения задач
По условию задачи дается прямоугольник, у которого известна ширина и высота. Ширина прямоугольника составляет 14 см, а его высота составляет 6 см. Необходимо найти периметр.
Решение
Для решения данной задачи необходимо применить следующую формулу: \(P=(L+W)\times2\). Исходя из этого \(P=(14+6)\times2=40\) сантиметров.
Ответ: 40 см.
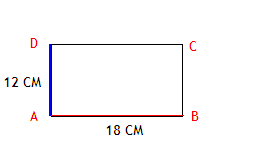
В прямоугольнике ABCD красная часть стороны является 18 сантиметров, синяя же часть стороны является 12 сантиметров. Необходимо найти периметр, выразить в сантиметрах.
Решение
Для того, чтобы решить данную задачу, необходимо принять во внимание, что противолежащие стороны прямоугольника являются равными. Тогда периметр будет рассчитываться так: \(2\times18+2\times12=36+24=60\)
Ответ: 60 сантиметров.
Длина прямоугольника равняется 28 сантиметров, ширина — на 6 сантиметров меньше. Нужно найти периметр прямоугольника, выразить в сантиметрах.
Решение
Изначально необходимо найти ширину прямоугольника. Она будет равна: 28-6=22 сантиметра. Зная ширину, теперь можно вычислить периметр: \(2\times(28+22)=2\times50=100\)сантиметров.
Ответ: 100 см.
Ширина прямоугольника равняется 19 сантиметров, в то время как длина прямоугольника в три раза больше, чем ширина прямоугольника. Нужно найти периметр прямоугольника, выразить в сантиметрах.
Решение
Для начала необходимо найти длину прямоугольника. Получается, что \(19\times3=57\) сантиметров. Периметр будет равен \(2\times(57+19)=2\times76=152\) сантиметров.
Ответ: 152 см.
Длина и ширина прямоугольника являются двумя последовательными числами. Необходимо найти ширину прямоугольника при условии, что известен периметр. Периметр прямоугольника равняется 30 сантиметров. Ширину прямоугольника нужно выразить в сантиметрах.
Решение
Итак, исходя из теории, нам известно, что периметр является \(2\times(ширина+длина)=30\). Получается, что ширина + длина = 30:2=15. Исходя из условий задачи, длина и ширина прямоугольника — последовательные числа, то есть 7+8=15. Таким образом ширина = 7.
Нам известно, что площадь равняется 18 см, соотношение прилежащих сторон равняется 1:2. Необходимо найти периметр прямоугольника.
Решение
Прилежащие стороны находятся в отношении 1 к 2. Необходимо ввести коэффициент пропорциональности x, после — выразить площадь. Так получится, что:
\(S=x\times{2x}=18\)
\(2x^{2}=18\)
\(x^{2}=9\)
\(x=3\)
Это означает, что одна сторона равняется 3, друга сторона в два раза больше, то есть 6. Периметр тогда будет рассчитываться так: 3+6+3+6=18.
Ответ: 18 см.
Длина прямоугольника равняется 6 сантиметров, ширина — на 2 сантиметра меньше, чем длина. Необходимо найти периметр.
Решение
Данную задачу возможно решить двумя способами. Первый способ:
- Ширина прямоугольника: \(6-2=4 см\).
- Половина периметра: \(6+4=10 см\).
- Периметр равняется \(10\times2=20 см\).
Второй способ:
Ширина равняется 6-2=4 см. \(P=2(a+b). P=2(6+4)=20 см\).
Ответ: 20 сантиметров.
Длина прямоугольника равняется 14 сантиметров. Чему будет равняться ширина, при условии, что периметр равняется 44 сантиметра?
Решение
- Половина периметра \(44\div2=22 см\).
- Ширина в таком случае будет \(22-14=8 см\).
Ответ: 8 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так