Как найти периметр круга по диаметру и радиусу: формулы, примеры
Что такое круг
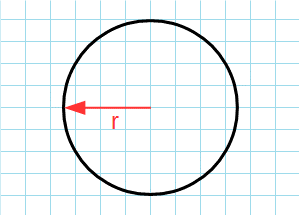
Кругом называют в геометрии расположение точек на плоскости, которые удалены от какой-то одной общей точки на расстояние, которое менее или равно заданному.
Окружность представляет собой замкнутую плоскую кривую, состоящую из набора множества точек, расположенных на одинаковом расстоянии от заданной точки, то есть центра, отмеченного на плоскости, аналогичной плоскости рассматриваемой окружности.
В учебниках по геометрии часто можно встретить и другое определение круга. Согласно этому понятию, он является сегментом плоскости, роль границ которого играет некая окружность. Отметим, что величина, характеризующая результат деления длины окружности на ее диаметр, является идентичной для всех окружностей. Это число \(\pi\), равное 3,14159…
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Периметром какой-либо геометрической фигуры называют сумму протяженностей ее границ.
Заметим, что размерность такого понятия, как периметр, аналогична размерности длины. По этой причине часто в примерах можно встретить понятия периметр или длина окружности.
Как найти периметр окружности
Существуют разные формулы для вычисления периметра окружности. Целесообразность применения в процессе решения задач того или иного справедливого соотношения параметров круга зависит от исходных условий. К примеру, рассчитать, чему равна длина окружности при известном радиусе можно с помощью такого уравнения:
\(P=2\pi r\)
В данном случае, \(\pi\) является постоянной величиной, которую при расчете округляют до значения 3,14, r обозначает радиус окружности.
Источник: mozgan.ru
Другой способ вычисления периметра круга заключается в применении следующей формулы с учетом значения радиуса:
\(P=\pi d\)
В данном случае, \(\pi\) является постоянной величиной, которую при расчете округляют до значения 3,14, d обозначает диаметр окружности.
Источник: mozgan.ru
Примеры
Имеется некая окружность. Радиус этой фигуры составляет 12 см. Необходимо вычислить, чему равен периметр круга.
Решение
Исходя из условия задачи, известен радиус. Таким образом, в процессе расчетов целесообразно воспользоваться первой формулой, а именно:
\(P=2\pi r \)
Подставим числовые значения и выполним вычисления:
\(P=2 \cdot 3,14 \cdot 12 = 75,36\)
Ответ: 75,36
Дан некий круг. Диаметр этой геометрической фигуры равен 15 см. Необходимо определить, чему в таком случае равен периметр окружности.
Решение:
Заметим, что в данной задаче известен диаметр. Поэтому следует воспользоваться второй записанной формулой и выполнить расчет, согласно данному соотношению:
\(P=\pi d\)
Подставим числовые значения и выполним вычисления:
\(P=\pi \cdot d = 3,14 \cdot 15 = 47,1\)
Ответ: 47,1
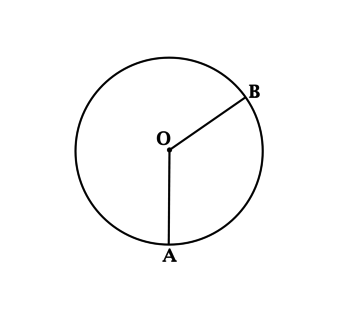
Дана некоторая окружность с центром, обозначенным за точку О. Ее периметр составляет 12, а градусная мера угла АОВ равна \(120^{\circ}\). С помощью точек А и В круг поделен на пару дуг. Требуется выяснить, чему равно отношение большей по размеру дуги к меньшей.
Источник: shkolkovo.net
Решение
Рассмотрим внимательно рисунок, на который перенесены условия задания. Заметим, что соотношение протяженностей дуг окружности соответствует тому, как относятся их градусные меры. Исходя из того, что точка О является центральной, можно сделать вывод о том, что угол АОВ центральный. Дуга, которая меньше по размеру по сравнению с полукругом, равна в градусах центральному углу, опирающемуся на эту дугу. В таком случае, руководствуясь условиями задачи, заключим, что самая маленькая из пары луг составляет \(120^{\circ}\). Вычислим градусную меру второй дуги:
\(360^{\circ} - 120^{\circ} = 240^{\circ}\)
Найдем отношения полученных величин:
\(\frac{240^{\circ}}{120^{\circ}} = 2\)
Ответ: 2.
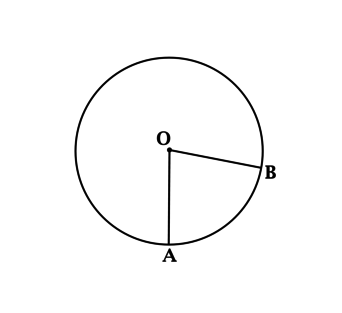
Дана некая окружность, центр которой совпадает с точкой О на плоскости. Ее длина соответствует 18 см. Сектор АОВ по площади равен\(\dfrac{18}{\pi}см^2\) . Необходимо вычислить, чему равна длина дуги АВ рассматриваемого сектора.
Источник: shkolkovo.net
Решение
Заметим, что определить длину окружности с известным радиусом можно по формуле:
\(2\pi R\)
Подставим в это выражение числовое значение, данное по условию задания:
\(С = 2\pi R = 18\)
В таком случае, радиус окружности равен:
\(R = \dfrac{9}{\pi} см\)
Если градусная мера дуги соответствует \(\alpha\), на которую опирается сектор, то его площадь можно вычислить таким образом:
\(\pi R^2 \cdot \dfrac{\alpha}{360}\)
Дуга в длину составляет:
\(С = 2\pi R\cdot \dfrac{\alpha}{360}\)
В результате длина дуги АВ равна:
\(С = \dfrac{18}{\pi} \cdot \dfrac{2\pi}{9} = 4\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так