Что нужно знать о периметре квадрата — основные сведения

Содержание:

Содержание

В представленной статье рассматриваются два вида нахождения периметра геометрической фигуры, для которой справедливы свойства прямоугольника — квадрата.

Что необходимо знать о квадрате

Квадрат — это правильный четырехугольник. Это значит, что у него все стороны равны и все углы равны 90°.

Все квадраты отличаются друг от друга только длиной стороны.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Основные свойства квадрата

все стороны фигуры равны;
фигура обладает симметрией;
все углы прямые;
взаимно перпендикулярные диагонали делятся точкой пересечения пополам, «разрезают» углы фигуры пополам, и при этом равны между собой.

Определение периметра

Периметром квадрата называют сумму длин всех его сторон: P = 4 × a.

Периметром считается длина стороны квадрата, умноженная на количество сторон.

Первый способ вычисления периметра квадрата

Очень легко высчитать периметр квадрата через его сторону.

В соответствии со свойствами квадрата, вычислить периметр можно четыре раза сложив известную длину стороны, т.е: \(а+a+a+a = P\). Либо, выполнить произведение: P = 4a.

Второй способ вычисления периметра квадрата

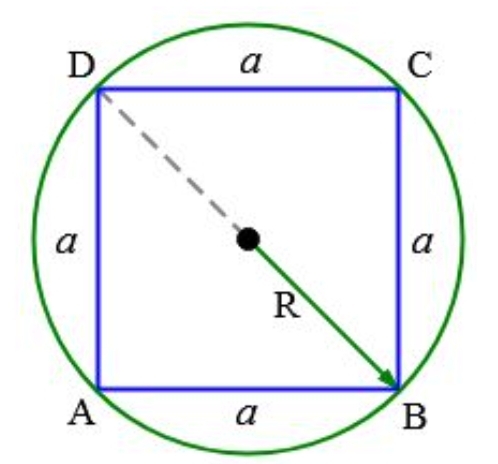
Вычислить периметр квадрата можно с помощью описанной окружности. В таком случае квадрат находится внутри окружности:

Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности.

Формула вычисления стороны квадрата находится через радиус описанной около квадрата окружности:

Формула 1

\(a=\sqrt{2}R\)

Тогда записать формулу периметра можно в таком виде:

Формула 2

\(a=\sqrt{2}R\times4\)

Примеры задач и их решение

Задача 1

Найти периметр квадрата, вписанного в окружность, если \(R = 4√2\).

Решить задачу несложно. Расчет будет основан на формуле стороны квадрата, вписанного в окружность: \(a=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\). Т. е. \(a=\frac{2R}{\sqrt{2}}\) Тогда периметр \(a=4\frac{2\times4\sqrt{2}}{\sqrt{2}}\)

Ответ: \(P = 4 ×8 = 32\).

Задача 2

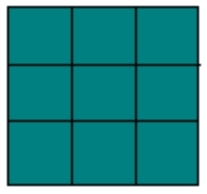
Периметр каждого из малых квадратов 12см. Как узнать периметр большого квадрата?

Решение: Так как периметр маленьких квадратов 12 см, то сторона квадрата равна 3 см. Сторона большого квадрата в три раза больше (на одну сторону большого квадрата приходится три стороны маленького), значит равна 9 см.

Периметр равен 9 · 4 = 36 см

Насколько полезной была для вас статья?

Рейтинг: 1.00 (Голосов: 1)

Заметили ошибку?

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»