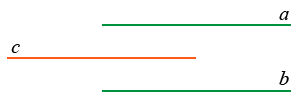Что нужно знать о параллельных прямых — основные сведения

Определение параллельности прямых

Родоначальниками геометрии как науки принято считать древних греков. В свое время, они переняли у египтян принцип измерения объемов тел и землемерия и превратили эти знания в научную дисциплину. На основании полученных знаний они сумели перейти к составлению общих закономерностей и описали их в доказательных трудах. Наиболее известный пример таких трудов — «Начала», написанные древнегреческим ученым Евклидом (III век до н. э.).

Аксиома о параллельных прямых, формулировка

При изучении свойств простых геометрических фигур, математики пользовались рядом теорем, доказанных ранее. Но некоторые утверждения в геометрии принимаются за исходные положения, на основании которых далее и доказываются теоремы. Такие исходные положения принято называть аксиомами. Вопрос о данной аксиоме или, как ее еще называют, пятом постулате Евклида, математики предпринимали попытки решить еще с давнего времени. Они хотели доказать данный постулат, т.е. вывести его из других утверждений. Но все их попытки потерпели неудачу. Лишь в прошлом веке математики окончательно выяснили, что данное утверждение не может быть доказано с помощью других аксиом, а само является ею. Русский математик Лобачевский Н. И. внес огромный вклад в решение этого вопроса. Итак, аксиому параллельных прямых можно сформулировать следующим образом:

Через точку, не лежащую на данной прямой, может быть проведена только одна прямая, параллельная данной.

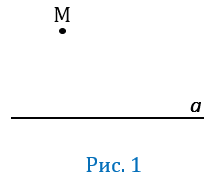
Для примера можно рассмотреть прямую а (проведенную произвольно) и не лежащую на ней точку (т.) М:

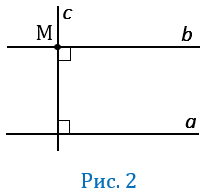
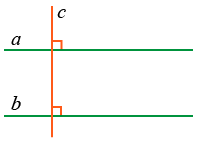
Проведем через т.М две прямые: сначала с перпендикулярно к а, а затем b перпендикулярно к с (Рис.2). Из того, что а и b перпендикулярны к c следует, что a || b.

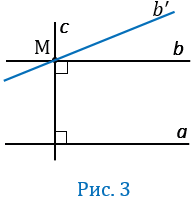
Теперь зададимся вопросом: можно ли через т.М провести другую прямую, которая так же будет || a? Если прямую b попробовать "повернуть" даже на незначительный угол вокруг т.М, то в бесконечности она пересечет a (рис.3).

То есть через т.М нельзя провести прямую, которая отличалась бы от b, и при этом не пересекающую a.

Утверждения, которые вытекают непосредственно из аксиом, называются следствиями:

1. Если прямая пересечет хотя бы одну из двух параллельных прямых, то она пересечет и другую.
2. Если две прямые параллельны третьей, то они параллельны.

Признаки параллельных прямых

Рассмотрим три признака параллельности прямых, связанных с разными видами углов.

Прямые параллельны если:

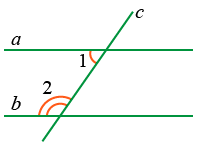
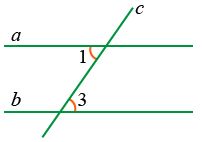
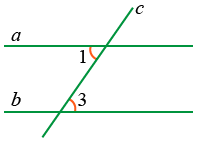
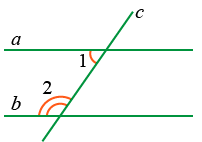
1. Сумма внутренних односторонних углов 180°

Если ∠1 + ∠2 = 180°, то  a || b.

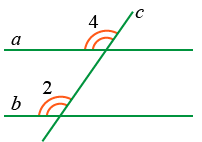
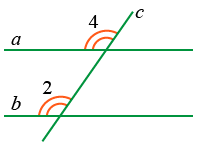
    2. Соответственные углы равны

Если ∠2 = ∠4,  то  a || b.

    3. Внутренние накрест лежащие углы равны

Если ∠1 = ∠3, то  a || b.

Свойства параллельных прямых

Свойства:

1. Через любую точку, не лежащую на прямой, можно провести только одну прямую, параллельную данной.
2. Если одна из параллельных прямых параллельна третьей, то и другая прямая параллельна третьей прямой.

Если а || b, b || c, то c || a 

1. Если прямая на плоскости перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой:

       Если  a || b  и  c ⊥ a,  то  c ⊥ b.

Теоремы об углах, образованных при пересечении двух прямых третьей прямой

1. Если две прямые пересечены секущей, то накрест лежащие углы равны.

Если  a || b,  то  ∠1 = ∠3.

    2. Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Если  a || b,  то  ∠2 = ∠4.

    3. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180⁰.

Если  a || b,  то  ∠1 + ∠2 = 180°.