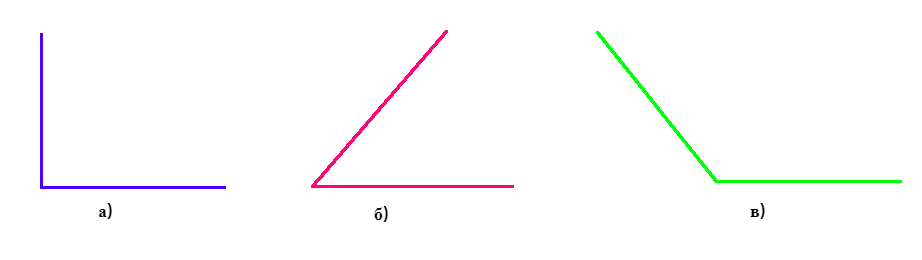Какой угол называется острым: определение, свойства, примеры
Что такое острый угол
Острым углом принято обозначать такой угол, который меньше по сравнению с прямым, то есть имеет градусную меру больше, чем ноль, но меньше, чем 90°.
Изобразим на рисунке, как выглядит острый угол, исходя из рассмотренного определения:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: www.treugolniki.ru
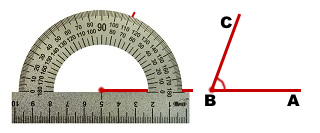
На уроках геометрии и математике при решении различных задач школьники пользуются специальными измерительными и чертежными инструментами. Одним из таких полезных приспособлений является транспортир. С его помощью можно достаточно быстро и просто выполнить построение острого угла какой-либо градусной меры.
Порядок действий при построении острого угла с применением транспортира:
- Отметить некую точку на листе бумаги, которая будет играть роль вершины заданного угла.
- Используя полученную точку, построить луч, вершина которого совпадает с ней. Данный луч является одной из сторон искомого угла.
- С помощью транспортира совместим вершину угла с отверстием, расположенным по центру инструмента, таким образом, чтобы отмеченный на нем ноль градусов совпал с определенной ранее стороной угла.
- Предположим, что необходимо рассмотренным способом начертить угол в 72°. На шкале транспортира в данном случае потребуется найти отметку в соответствии с заданной градусной мерой и нарисовать точку.
- Далее следует соединить полученную точку с вершиной угла с помощью луча, который является второй стороной искомого угла.
Перенесем рассмотренную схему изображения острого угла в 72°. Заметим, что отчет градусной меры допустимо начинать с нижней или верхней шкалы, отмеченной на транспортире:
Источник: www.treugolniki.ru
Признаки и свойства острых углов
Перечислим свойства, которые характерны для любого острого угла:
- При рассмотрении пары смежных углов, один из которых меньше по сравнению с прямым, то есть определяется как острый, можно сделать вывод, что второй из смежных углов является тупым.
- Какой-либо произвольный треугольник обладает как минимум одним острым углом.
- Треугольники, которые образованы тремя острыми углами, носят название остроугольных.
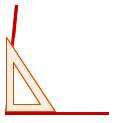
Признаком любого острого угла является его градусная мера, которая в любом случае будет меньше, чем 90°. В геометрии часто встречаются задачи, когда необходимо идентифицировать тот или иной угол по его признаку. Тогда целесообразно воспользоваться еще одним полезным инструментом под названием угольник.
В качестве примера воспользуемся угольником и соединим его вершину с вершиной искомого угла, который необходимо идентифицировать. При этом расположим угольник так, чтобы его грань проходила по какой-нибудь одной стороне рассматриваемого угла. В результате другая сторона измерительного инструмента перекроет вторую сторону угла. Изобразим схематично принцип выполнения этой процедуры:
Источник: www.treugolniki.ru
Примеры решения задач
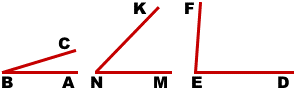
На рисунке изображено несколько углов.Требуется выяснить, какой из представленных углов является острым.
Решение
Воспользуемся определением острого угла и вспомним, что его градусная мера меньше, чем 90°.
Рассмотрим изображение угла на рисунке (а). Заметим, что в данном случае одна сторона угла играет роль перпендикуляра по отношению ко второй. Тогда угол, который расположен между ними, составляет 90°. Сделаем вывод, что такой угол является прямым.
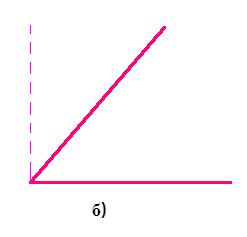
Далее обратимся к рисунку (б). Построим к одной из сторон угла перпендикуляр. Изобразим это действие наглядно, дополнив начальное изображение:
Заметим, что угол меньше по сравнению с прямым. Это утверждение полностью соответствует понятию острого угла. Сделаем вывод о том, что угол, изображенный на рисунке (б), является острым.
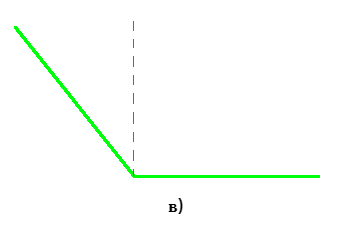
Перейдем к третьему варианту. Аналогично предыдущему примеру, построим перпендикулярную прямую к углу, изображенному на рисунке (в), которая проходит через его вершину:
Заметим, что искомый угол больше по сравнению с прямым, то есть имеет такую градусную меру, которая превышает 90°. Данный угол можно идентифицировать как тупой. Он не является острым.
Ответ: острым является угол, изображенный на рисунке (б).
Имеется пара смежных углов. Один из них имеет градусную меру, которая на 30° меньше, чем у второго. Необходимо определить, чему равен острый угол.
Решение
Введем обозначение х для неизвестного острого угла. В таком случае угол, градусная мера которого больше, можно записать в виде следующего выражения:
х + 30
Вспомним, что острый угол обладает полезным свойством. При рассмотрении пары смежных углов, один из которых меньше по сравнению с прямым, то есть определяется как острый, можно сделать вывод, что второй из смежных углов является тупым. В сумме смежные углы составляют 180°. Запишем справедливое равенство:
х + (х+30) = 180
2х = 150
х = 75
Угол, который ранее был обозначен за х, составляет 75°. Заметим, что такая градусная мера меньше, чем 90°. На основании этого факта острый угол равен 75°.
Ответ: 75°.
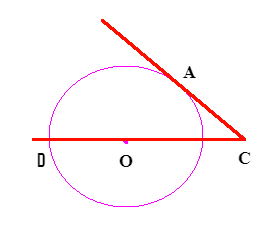
На рисунке изображена окружность с центром в точке О. К окружности построена касательная СА, которая играет роль одной из сторон угла с вершиной в точке С. Вторая сторона угла пересекает точку О. Градусная мера полученной дуги АD составляет 100°. Необходимо вычислить, чему равен угол АСО.
Решение
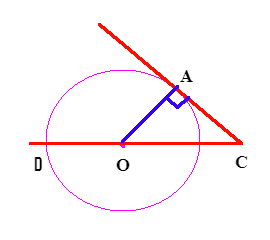
Построим в заданной окружности радиус, который обозначим как ОА. Перенесем действия на рисунок:
Заметим, что полученный треугольник АОС имеет прямой угол, то есть по определению является прямоугольным:
АОС = 90°
Вспомним, что в сумме все углы в треугольнике составляют 180°. На основании этого соотношения вычислим градусную меру угла СОА:
СОА = 180 – АОD = 180 – 100 = 80
В результате угол АОС составит:
АОС = 90 – 80 = 10
Ответ: 10°
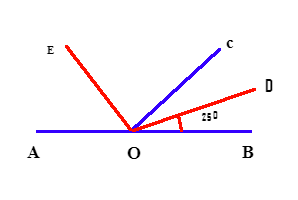
На рисунке изображены два смежных угла. Необходимо вычислить, чему равен угол АОЕ при условии, что ОЕ является биссектрисой угла АОС. Аналогично, ОD играет роль биссектрисы угла СОВ. Градусная мера угла ВОD составляет 25°. Необходимо вычислить угол АОЕ.
Решение
Исходя из того, что биссектриса делит угол на две равные части, вычислим градусную меру угла СОВ:
СОВ = \(25 \cdot 2\) = 50
Развернутый угол АОВ составляет 180° по определению. Тогда можно найти величину угла АОС:
АОС = 180 – 50 = 130
Зная, что биссектриса ОЕ делит угол АОС на два равных угла, получим, что искомый угол АОЕ равен:
АОЕ = \(130 \div 2\) = 65
Ответ: 65°.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так