Как найти область значения функции

Понятие области значения функций

Какая-либо функция подразумевает пару видов переменных в формуле, то есть тех, которые зависят или не зависят от нее. Стоит отметить, что х считают независимой, так как эта переменная обладает возможностью принимать любые значения. Исключением являются величины, обращающие функцию в пустое множество. Это условие важно учитывать в процессе решения задач, чтобы не допускать подобных ситуаций. Переменных, которые не зависят от функции, может быть несколько. По этой причине при проведении вычислений примеров нужно обнаружить все возможные величины переменной.

Предусмотрено обозначение для рассматриваемых точек: M (x;f(x)). При изображении функции на графике, то есть соединении всех ее точек образуется линия определенной формы в зависимости от разновидности функции. Получается, что область значений функции, обозначает некое множество, в состав которого включены все величины, принимаемые заданной функцией.

Как найти множество значений функции

Как правило, при решении задач часто требуется выявить множество величин, соответствующих конкретной функции, то есть определить ее область значений. На первый взгляд задание кажется сложным. Однако предусмотрено несколько эффективных методик для поиска ответа на этот вопрос. В целом, можно выделить пару ключевых способов, то есть:

• программный;
• ручной.

Первый принцип поиска области значений применим к любым типам функций. Реализация метода предполагает автоматизацию, то есть использование специального программного обеспечения, к примеру, профильных программ и приложений. Пользователю остается лишь внести исходные данные в калькулятор, и компьютер выдаст ответ с высокой точностью и без ошибок.

Второй вариант решения задания предусматривает применение теоретических знаний на практике. С помощью действенных методик и правил можно справиться с заданиями на исследование функциональных зависимостей самостоятельно без автоматизированных средств. В процессе придется проявить внимательность и логическое мышление, так как важно с высокой точностью исключить все лишние значения переменных. В результате ответ будет сформулирован без погрешностей. Перечислим распространенные способы формирования области значений функции:

• индивидуальное определение величин каждого компонента сложной функциональной зависимости;
• метод оценки;
• использование свойств функции быть монотонной и не прерываться на графике;
• вычисление производной;
• применение максимальных и минимальных значений.

В некоторых заданиях от ученика требуется вычислить E (f) для какой-либо функциональной зависимости, относящейся к сложному типу. Подобная конфигурация предполагает громоздкие расчеты и высокую вероятность совершения ошибок.  По этой причине задание предварительно делят на отдельные этапы. Подобная методика демонстрирует высокую эффективность в написании самостоятельных и контрольных работ по алгебре, а также нашла широкое применение в профессиональных и прикладных сферах, к примеру, экономике, менеджменте, архитектуре. Последовательный поиск области значений функциональной зависимости представляет собой выполнение следующего алгоритма действий:

• переписать представленное соотношение в более простой вид;
• выделить в записи отдельные компоненты;
• найти область значений индивидуально для каждого из определенных ранее элементов;
• воспользоваться приемом замены;
• проанализировать полученный результат;
• зафиксировать итог решения.

Следующий способ вычисления E (f) заключается в проведении оценочного анализа. В процессе рассматриваемую функциональную зависимость нужно оценить по направлениям вверх и вниз.  Параллельно с этим потребуется представить доказательства факта достижения функцией заданных границ. Методика несколько легче с точки зрения вычислений по сравнению с первым рассмотренным методом. В этом случае потребуется лишь:

• сформулировать доказательства непрерывности функции;
• сопоставить неравенства для нескольких функциональных зависимостей;
• оценить полученные результаты;
• определить интервал для записи в ответ.

К простейшим методикам расчета границ области, которую составляют значения функции, относят анализ непрерывности и монотонности функциональной зависимости. Вычисления не отнимут много времени и сил, если знать и уметь пользоваться инструкцией, описывающей действия при решении задачи пошагово:

• упрощение соотношения;
• замена величин при возникновении такой необходимости;
• определение вершины на графическом изображении функции;
• выявление промежутка;
• поиск самых маленьких и больших значений;
• формулировка области величин.

Следующие два способа в распространенных случаях объединяют в один алгоритм действий. В процессе учитывают найденную производную, а также минимальное и максимальное значение для конкретной функциональной зависимости. Последовательность шагов:

• вычисление производной;
• исследование функции;
• выявление наибольшей и наименьшей точки;
• запись интервала искомых значений.

Примеры решения задач

Решение

С целью вычисления искомых величин нужно составить сразу пару неравенств и записать общий ответ:

\(1+х\geq 0\)

4-х > 0

\(х \geq -1\)

х < 4

\(-1 \leq х < 4\)

Источник: lc.rt.ru

Ответ: \(х\in [ -1;4)\)

Дополнительно необходимо представить графическое изображение функциональной зависимости.

Решение

Область определения задается неравенством:

\(16-х^{2} \geq 0 \Leftrightarrow (4-х)(4+х) \geq 0 \Leftrightarrow -4 \leq х \leq 4\)

Под корнем имеем функцию:

\(u(х) = 16-х^{2}\)

Заметим, что в данном случае переменная соответствует следующим значениям:

\(х\in \left[-4; 4 \right]\)

Область значения этой функции:

\(u\in \left[0; 16 \right]\)

Рассмотрим следующее условие, вытекающее из предыдущих расчетов:

\(у = \sqrt{u} \)

В результате получим, что:

\(у\in \left[0; 4 \right]\)

Таким образом:

\(Е(f) = \left[0; 4 \right]\)

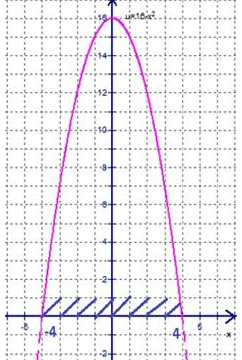
Графическое изображение функциональной зависимости \(u = 16-х^{2}\)

Источник: lc.rt.ru

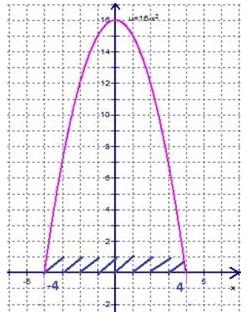
Далее представим график функциональной зависимости \(u = 16-х^{2}\) при соблюдении выявленного в процессе расчетов условия, а именно, когда \(х\in \left[-4; 4 \right]\)

Источник: lc.rt.ru

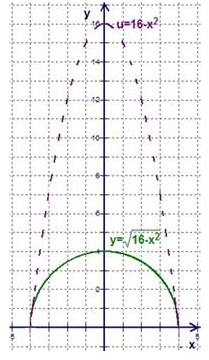
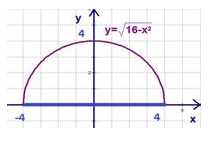
Схематичное изображение графика функции \(у = \sqrt{16-х^{2}}\)

Источник: lc.rt.ru

\(u(х) = 16-х^{2}, х\in \left[-4; 4 \right], u\in \left[0; 16 \right]\)

\(у = \sqrt{16-х^{2}}, х\in \left[-4; 4 \right], у\in \left[0; 4 \right]\)

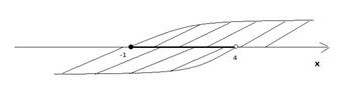
На примере данной функции иллюстрируется связь между областью значения, областью определения и графиком. Проекция графика функции \(у = \sqrt{16-х^{2}}\) на ось х представляет собой область определения:

\(х\in \left[-4; 4 \right]\)

Графически подобный вывод можно сформулировать следующим образом:

Источник: lc.rt.ru

Область значений функции \(у = \sqrt{16-х^{2}}\) представляет собой проекцию графика на ось у.

Решение

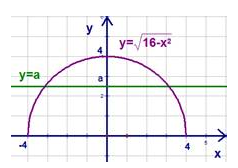
Попробуем найти ответ к этой задаче графическим способом. Нужно воспроизвести в памяти алгоритм построения графика для рассматриваемой в рамках упражнения функциональной зависимости. Выполним необходимые построения и продолжим решение примера.

Источник: lc.rt.ru

Пересечение прямой у=а  и графика функции существует тогда и только тогда, когда \(а\in \left[0; 4 \right]\). Основываясь на результатах логического заключения можно записать ответ к задаче.

Ответ: \(а\in \left[0; 4 \right].\)

Решение

В первую очередь вычислим, какие значения может принимать х для существования функции.

При значении \(x^2>16\) под корнем получается отрицательное число, а это значит, что область определения функции от [-4;4] включительно.

На следующем этапе целесообразно приступить к поискам производной рассматриваемой функциональной зависимости:

\((\sqrt{16-x^2})’=-\frac{x}{\sqrt{16-x^2}}\)

Если в знаменателе производной нуль, то производной не существует, в данном случае это условие выполняется при x=±4.

Приравниваем производную к нулевому значению и вычисляем х. Производная записанной функциональной зависимости принимает нулевое значение при x=0. Далее методом подстановки запишем вычисленные ранее значения производной в начальную функцию. В результате получим, что минимальное значение функции составит:

f(4) и f(-4)

Если выполняются обозначенные выше условия, то функциональная зависимость принимает нулевое значение. Запишем максимальное значение, характерное для этой функции: x=0. В этой точке функция равна 16.

Ответ: \(Е(f) = \left[0; 4 \right]\)

Решение

Проанализируем данную функцию. Так как минимальное значение синуса равно минус единице, а а максимальное составляет единичное значение, то путем подстановки в исходное соотношение обозначенных значений получаем, что:

\(max(f(x))=10\)

\(x=\frac{3π}{2}\)

\(min(f(x))=2\)

\(x=\frac{π}{2}\)

Таким образом, путем несложных вычислений получен ответ к задаче.

Ответ: приемлемые значения для указанной функции соответствуют следующему множеству E(x)=[2;10].