Область определения арккосинуса

Что такое арккосинус

Арккосинус представляет собой функцию, которая является обратной для тригонометрической функции косинуса. Наименования подобных функций сложились из преобразования названий функций тригонометрии путем записи в начале приставки «арк». В переводе с латинского языка словом arcus называют дугу. Объяснить это можно, если рассмотреть приведение геометрического смысла обратной функции в тригонометрии, связанной с протяженностью дуги единичной окружности, либо углом, который стягивает данную дугу и соотнесен с тем или иным отрезком.

В результате получается, что стандартный синус помогает вычислить хорду, зная дугу, которая ее стягивает. С помощью обратной функции несложно выполнить противоположное действие. Такой принцип обозначения обратных функций в тригонометрии ввел математик из Австрии Карл Шерфер в восемнадцатом веке. Традицию поддержал Лагранж.

Определить арккосинус для некоторого числа х можно через функцию, которая является обратной к косинусу данного х. При этом должно выполняться следующее условие:

\(-1 \leq х \leq 1\).

В том случае, когда косинус какого-то угла у соответствует значению х, то есть соs у = х, тогда арккосинус х можно находить по значению у:

\(arccos x = cos^{-1} x = y\)

Сформулируем важное условие, которое необходимо принимать во внимание при выполнении расчетов. В данном случае \(cos^{-1} x\) является обозначением обратного косинуса. Не стоит интерпретировать эту запись как косинус в минус первой степени. Рассмотрим наглядный пример вычислений с уравнением:

\(arccos 1 = cos^{-1} 1 = 0° (0 рад)\)

Свойства арккосинуса

Как и обычные, обратные тригонометрические функции обладают рядом характерных свойств. Благодаря таким закономерностям, значительно упрощается решение различных задач в физике, алгебре, геометрии и других точных науках. Перечислим основные свойства с формулами:

1. \(\arccos(-x)=\pi -\arccos x\). Функция является центрально-симметричной по отношению к точке с координатами \(\left(0;{\frac {\pi }{2}}\right)\)и индифферентной, то есть ни четной, ни нечетной.
2. \(\arccos x>0\) при условии, что \(-1\leqslant x<1\).
3. \(\arccos x=0\) при условии, что x=1.
4. \(\arccos x={\frac {\pi }{2}}-\arcsin x\).
5. \(\arccos x=\left\{{\begin{matrix}\arcsin {\sqrt {1-x^{2}}},\qquad 0\leqslant x\leqslant 1\\\pi -\arcsin {\sqrt {1-x^{2}}},\qquad -1\leqslant x<0\end{matrix}}\right.\)
6. \(\arccos x=\operatorname {arcctg} {\frac {x}{\sqrt {1-x^{2}}}}\)
7. \(\arccos x=\left\{{\begin{matrix}\operatorname {arctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad 0<x\leqslant 1\\\pi +\operatorname {arctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad -1\leqslant x<0\end{matrix}}\right.\)

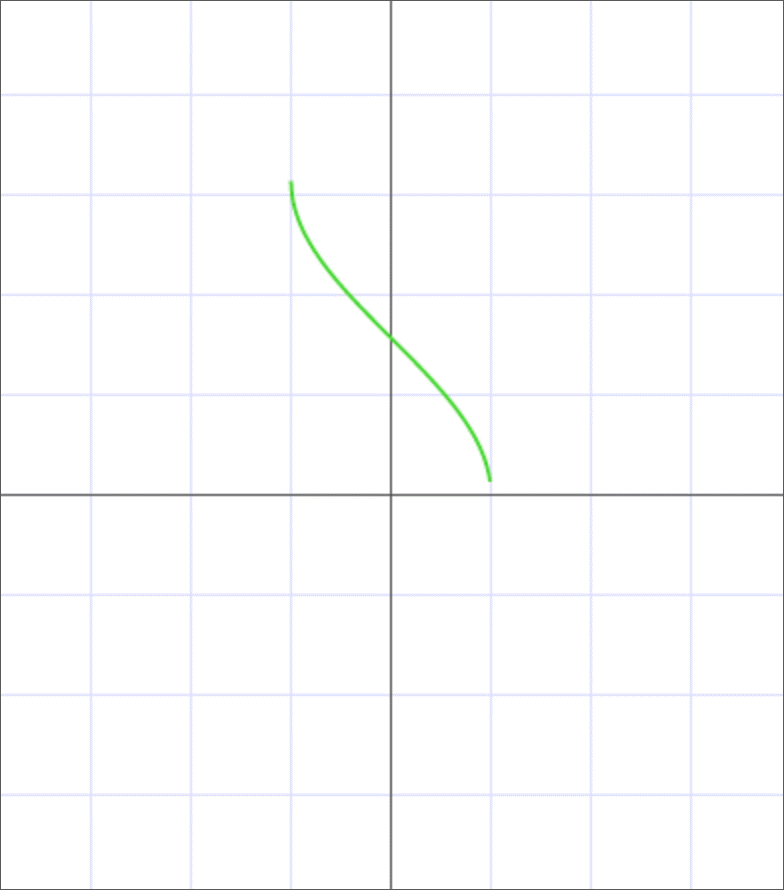
График арккосинуса

Представим наглядное изображение арккосинуса на графике:

Источник: microexcel.ru

Как вычислить арккосинус

Представим, что имеется некоторая функция \(y=\cos x\). Если рассмотреть область, на которой эта функция определяется, то можно заметить, что она кусочно-монотонная. Таким образом, обратное соотношение \(y=\arccos x\) нельзя назвать функцией. По этой причине целесообразно взять для анализа отрезок, на котором функция является строго убывающей и принимает каждое из своих значений: \([0;\pi ]\) .

На рассматриваемом отрезке \(y=\cos x\) является строго монотонно убывающей и принимает каждое из своих значений единственный раз. На основании вышесказанного можно сделать вывод о том, что на отрезке \([0;\pi ]\) имеется обратная функция \(y=\arccos x\). Графически эта функция расположена симметрично по отношению к изображению \(y=\cos x\) на отрезке \([0;\pi ]\) относительно прямой линии, соответствующей выражению у=х.

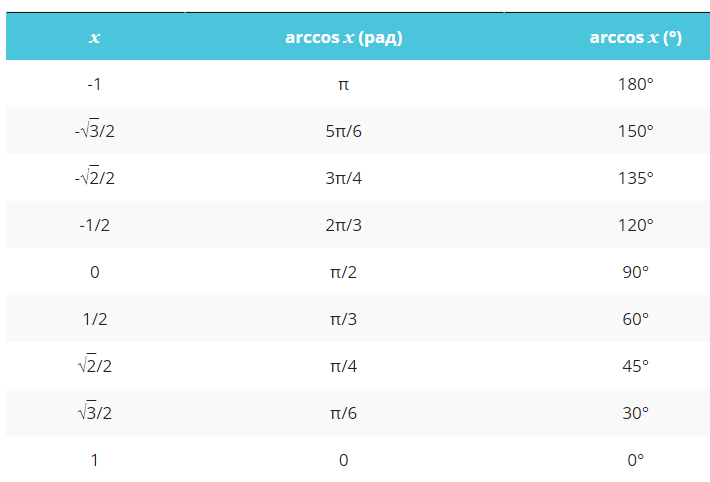
Таблица арккосинусов

Источник: microexcel.ru