Объем призмы: как вычислить, формула
Что такое призма
Самой популярной сферой применения призм является оптика. С помощью элементов такой геометрической формы инженеры проектируют оптические устройства и аппаратуру, к примеру, телескопы, бинокли, микроскопы, оборудование, предназначенное для фиксации изображений, генерируемых электроникой, и реализации широкого спектра функций, спектральная оптика, интерферометры, поляриметры и прочие измерители. Благодаря применению призм в технике, сконструированной на основе чувствительной оптики, получается менять направление излучения, осуществлять оборот и перенос изображений, дифференцировать лучевые пучки, формировать спектр, проводить разные исследования и анализы.
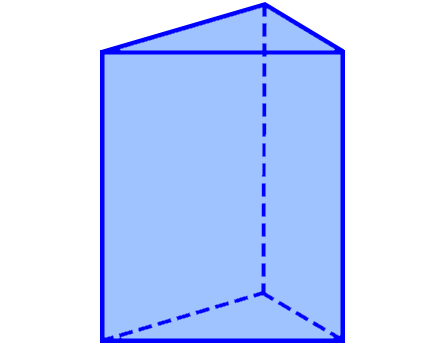
Призма представляет собой геометрическую фигуру с каким-то количеством граней, то есть является многогранником с равными двумя гранями в виде многоугольников, которые расположены в плоскостях, ориентированных параллельно друг относительно друга, и другими гранями в виде параллелограммов, обладающих едиными сторонами с данными многоугольниками.
В призме выделяют составные элементы. В качестве основных частей фигуры, которые часто встречаются при решении задач по геометрии, выделяют боковые грани, роль которых играют параллелограммы. Пара многоугольников, о которых идет речь в определении призмы, являются основаниями геометрической фигуры.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В зависимости от вида многоугольника, расположенного в основании, формулируют наименование призмы, к примеру:
- если основание является треугольником, то призму называют треугольной;
- призма с четырехугольником в виде основания представляет собой четырехугольную призму;
- когда основание имеет вид пятиугольника, призма является пятиугольной.
Призма напоминает геометрическую фигуру под названием цилиндр. В действительности призма является частным случаем некругового цилиндра.
Рассмотрим элементы призмы:
- основаниями называют пару граней в виде равных многоугольников, которые ориентированы параллельно друг другу;
- боковые грани представляют собой такие грани призмы, которые не являются основаниями;
- боковая поверхность объединяет боковые грани;
- полная поверхность объединяет основания и боковую поверхность;
- боковыми ребрами называют общие для граней с боков призмы стороны;
- высотой обозначают отрезок, с помощью которого соединены плоскости оснований геометрической фигуры и который является перпендикуляром к этим основаниям;
- диагональ представляет собой отрезок, с помощью которого соединены пара вершин геометрической фигуры, не имеющих общей грани;
- диагональная плоскость проходит через боковое ребро призмы и пересекает диагональ основания;
- диагональным сечением называют пересечение призмы с диагональной плоскостью, что сопровождается образованием параллелограмма, к примеру, ромба, прямоугольника, квадрата;
- перпендикулярное сечение представляет собой пересечение призмы с плоскостью, которая расположена перпендикулярно относительно бокового ребра этой призмы.
Источник: ru.wikipedia.org
Как найти объем призмы
Объемом называют количественный параметр, характеризующий пространство, которое занимает некое тело или вещество.
При решении задач по физике и геометрии часто встречаются примеры на вычисление объема. Данное понятие перекликается с термином вместимости. Как правило, школьникам предлагается рассчитать, чему равен объем внутри резервуара, упаковочной коробки и подобные величины.
С древних времен ученых интересовали разнообразные формы материальных тел, в том числе, тех, которые имеют вид призмы. Процесс исследования заключался в изучении наиболее сложных фигур и переходу к самым простым. Подобный метод просматривается в трудах Евклида. Обратный способ проведения научных изысканий характерен для работ Герона Александрийского.
Объем какого-то тела зависит от следующих его параметров:
- форма;
- линейные размеры.
Ключевое свойство объема заключается в том, что это аддитивная величина. Понимать это утверждение следует, как равенство объема некого тела сумме объемов, которыми обладают непересекающиеся между собой фрагменты рассматриваемого тела.
Объем призмы является результатом умножения площади основания этой геометрической фигуры на ее высоту.
Главная формула
Запишем основную формулу, с помощью которой принято вычислять объем призмы при известных величинах высоты и площади основания рассматриваемой фигуры:
\(V=S\cdot h\)
В том случае, когда призма обладает правильным n-угольным основанием, для вычисления ее объема целесообразно воспользоваться несколько видоизмененным математическим соотношением:
\(V={\frac {n}{4}}hs^{2}\mathrm {ctg} {\frac {\pi }{n}}\)
Заметим, что s в данном случае является обозначением длина стороны многоугольника.
Записанные соотношения удобно применять в процессе решения задач по геометрии и физике. Это значительно упрощает расчета. Вместо громоздких и трудоемких измерений можно быстро найти объем по известным величинам, которые также можно измерить, вычислить по средствам других известных элементов геометрической фигуры, выразить из условия заданий. Рассмотрим несколько типичных примеров.
Архитектурные достопримечательности древнего Вавилона и Египта состоят из различных геометрических фигур, в том числе, имеют в своей конструкции призмы. Таким образом, можно объяснить острую необходимость в вычислении объемов материальных тел, выполненных в форме призмы. Буквальный перевод этого распространенного в стереометрии понятия означает «отпиленное» тело.
Дана некая геометрическая фигура, которая имеет форму призмы. Данное тело в пространстве обладает основанием, равным 14 кв. см. Высота рассматриваемой призмы составляет 6 см. На основании исходных данных требуется вычислить, чему равен объем этой призмы.
Решение
Воспользуемся уже известной формулой для вычисления объема. Она имеет следующий вид:
\(V=S\cdot h\)
Путем подстановки известных величин выполним преобразование стандартной формулы и вычислим искомый объем фигуры:
\(V = 14 \cdot 6 = 84\)
Ответ: 84 кв. см.
Имеется некая призма, которая занимает в пространстве объем, равный 106 кв. см. Площадь основания, которым обладает рассматриваемая геометрическая фигура, равна 10 кв. см. Требуется вычислить, чему равна высота данной призмы.
Решение
Воспользуемся рассмотренной ранее формулой для вычисления объема геометрической фигуры в виде призмы. Запишем справедливое соотношение:
\(V=S\cdot h\)
Заметим, что по условию задания известны величины объема и площади основания призмы. Перепишем уравнение таким образом, чтобы высота оказалась в левой части соотношения:
\(h = \frac{V}{S}\)
Подставим известные значения в полученное равенство, чтобы вычислить, чему равна высота рассматриваемой геометрической фигуры:
\(h = \frac{106}{10} = 10,6\)
Ответ: 10,6 см.
На столе расположена некая емкость, которая выполнена в форме правильной треугольной призмы. Данный резервуар заполнили жидкостью в количестве 2300 кв. см. В емкость погрузили какую-то конструкцию, что спровоцировало подъем уровня с 25 см до 27 см. Требуется вычислить, какой объем имеет эта конструкция.
Решение
Воспользуемся закономерным соотношением, согласно которому справедливо равенство объемов, которые соответствуют погруженной конструкции и вытесненной воды из сосуда. Количество жидкости, которая была вытеснена, соответствует 2/25 от начального объема. Таким образом, можно записать следующее выражение:
\(V_дет = \frac{2}{25}\cdot 2300 = 184\)
Ответ: 184 кв. см.
Прямая треугольная призма имеет основание в виде треугольника, один из углов которого составляет 90 градусов. Катеты рассматриваемого треугольника равны 6 и 8 соответственно. Значение бокового ребра составляет 5. Требуется вычислить, чему равен объем призмы.
Решение
С помощью уже знакомых теоретических закономерностей запишем уравнение для вычисления объема рассматриваемой призмы:
\(V = S \cdot h\)
Вернемся к условию задачи и подставим числовые значения в полученную формулу, чтобы получить искомый результат:
\(V = \frac{1}{2} \cdot 6 \cdot 8 \cdot 5 = 120\)
Ответ: 120 кв. см.
Резервуар по форме соответствует правильной треугольной призме. Данную емкость заполнили водой до некого уровня, высота которого составляет 80 см. Имеется вторая емкость со стороной основы, превышающей в 4 раза сторону основания первого сосуда. В эту пустую емкость перелили жидкость из первого резервуара. Нужно вычислить уровень, на котором вода будет находиться во втором сосуде.
Решение
Воспользуемся формулами, уже знакомыми из курса теории, а именно, соотношением, позволяющим определить объем фигуры в виде призмы^
\(V = \frac{\sqrt{3}a^{2}}{4}\)
Выразим из полученного соотношения высоту, которая определяется следующим образом:
\(Н = \frac {4V}{\sqrt{3}a^{2}}\)
Заметим некую зависимость между стороной основания и высотой. Если первую величину увеличить в 4 раза, то это приведет к увеличению знаменателя в полученном соотношении в 16 раз. В таком случае, исходя из условий задачи, можно наблюдать уменьшение значения высоты в 16 раз. Таким образом, уровень, на котором жидкость находится во второй емкости, составляет 5 см.
Ответ: 5 см.
Имеется некая треугольная призма, характеризующаяся объемом, равным 32. В основе этой фигуры построена средняя линия. Данную линию пересекает плоскость, расположенная параллельно по отношению к боковому ребру призмы. Требуется определить, чему равен объем полученной геометрической фигуры, то есть отсеченной треугольной призмы.
Решение
Заметим, что в условии задания говориться об уменьшении элементов треугольника, являющегося основанием начальной призмы, таких как, высота и основание, в два раза. Таким образом, основание части, которая была отсечена от исходной фигуры, по площади меньше начального основания в 4 раза. При имеющихся условиях высота призмы не поменялась. Запишем уравнение для вычисления объема призмы через площадь ее основания и высоту:
\(V = S \cdot h\)
В результате можно прийти к выводу о том, что при стабильном значении высоты объем фигуры станет меньше в 4 раза по сравнению с объемом исходной призмы.
Ответ: 4.
Объем правильной треугольной призмы
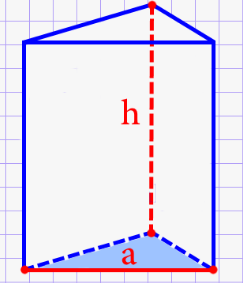
Правильная призма представляет собой такую призму, которая является прямой с основанием в виде правильного многоугольника.
В правильной призме боковые грани имеют вид прямоугольников, которые равны между собой. Объем правильной треугольной призмы принято вычислять через известные значения ребра и высоты рассматриваемой геометрической фигуры.
Источник: max-calc.ru
Объемом правильной треугольной призмы является физической величиной определенного участка пространства, занятого правильной треугольной призмой, и вычисляется, как результат умножения площади основания на высоту этой геометрической фигуры.
Источник: max-calc.ru
Формула для определения объема правильной треугольной призмы имеет следующий вид:
\(V=\frac{a^{2}}{4}\cdot h\sqrt{3}\)
В данном случае а является стороной граней призмы, то есть ребром, h обозначает высоту геометрической фигуры.
Объем правильной четырехугольной призмы
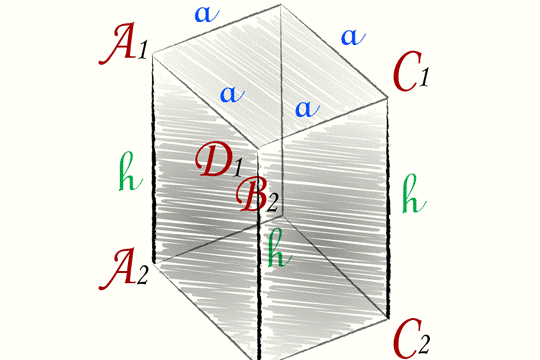
Правильная четырехугольная призма представляет собой такую призму, основание которой является правильным четырехугольником, то есть имеет вид квадрата.
Источник: www.fxyz.ru
Рассчитать объем, которым обладает правильная четырехугольная призма, можно путем умножения площади квадрата, играющего роль основания призмы, и высоты этой геометрической фигуры.
Формула, которую используют для определения объема правильной четырехугольной призмы, имеет следующий вид:
\(V = a^{2} h\)
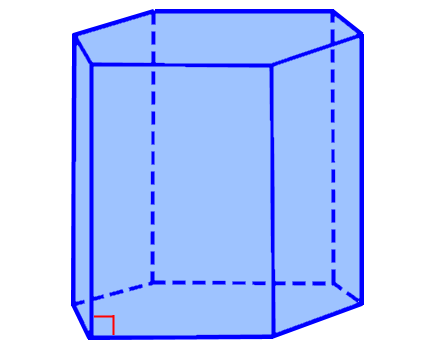
Объем правильной шестиугольной призмы
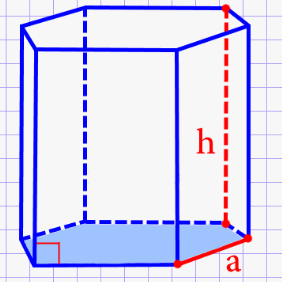
Рассмотрим следующий тип призмы, которую называют правильной шестиугольной. Изображение данной геометрической фигуры имеет следующий вид:
Источник: max-calc.ru
Объем, который занимает в пространстве фигура в виде правильной шестиугольной призмы, представляет собой физическую величину, характеризующую эту часть пространства. Вычислить данную характеристику можно путем умножения площади основания и высоты призмы.
Источник: max-calc.ru
Формула, которую целесообразно использовать в процессе решения задач на нахождение объема правильной шестиугольной призмы, имеет следующий вид:
\(V=\frac{3a^{2}}{2}\cdot h\sqrt{3}\)
В данном случае а является стороной граней призмы, то есть ребром, h обозначает высоту геометрической фигуры.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так